Лінійні алгоритми.

Лінійними називають алгоритми, які забезпечують отримання результату однократним виконанням послідовності дій незалежно від початкових даних чи від проміжних результатів. В лінійних алгоритмах відсутні логічні блоки. Блокові символи в цій структурі розташовуються в тому ж порядку, у якому повинні бути виконані дії, що приписуються ними. Такий порядок виконання дій називають природним.

Приклад 2.1. Скласти алгоритм обчислення виразу y= a+ d * c.

Весь процес обчислення виразу виглядає так:

1. Транслятор відводить три комірчини пам’яті для змінних a, d, c.

2. При введенні значення змінних записуються у відведені комірчини пам’яті. Нехай це буде a=1, d=2, c=3.

3. Далі в АЛУ процесора дублюються значення d та c, відбувається множення, потім дублюється значення a та додається до добутку.

4. Одержаний результат записується в комірчину, відведену транслятором для змінної y.

5. По команді виведення на екрані з’являється значення y.

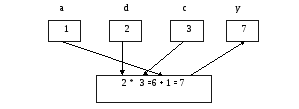
Зобразимо алгоритм у вигляді блок-схеми:

Приклад 2.2. Задані два дійсних числа. Знайти їх суму, різницю та добуток.

Для кожної величини, йдеться мова в прикладі , введемо ідентифікатор.

Таблиця 2.3. Таблиця опису величин.

Величина	Ідентифікатор	Тип
	Вхідна величина
Перше число	a	Дійсний
Друге число	b	Дійсний
	Результат
Сума	S	Дійсний
Різниця	R	Дійсний
Добуток	P	Дійсний

Складемо алгоритм:

Приклад 2.3. Задано дві величини a та b. Поміняти місцями їх значення.

Для розв’язання задачі будемо використовувати третю, допоміжну величину х. Обмін відбувається наступним чином:

Спочатку величині х треба присвоїти на деякий час значення величини a, потім величині a присвоїмо значення величини b, а в кінці величині b присвоїмо значення величини х, яка зберігає початкове значення величини a.

Складемо блок-схему алгоритму:

Лінійні програми.

З поняттям лінійного обчислювального процесу ви ознайомилися в першому розділі. Тепер ми знаємо декілька основних операторів мови Pascal. Їх буде достатньо, щоб описати лінійний алгоритм на мові Pascal. Розглянемо декілька прикладів.

Приклад 3.1.Задані катети прямокутного трикутника. Знайти його гіпотенузу та площу.

Спочатку визначимося з даними. Вхідними є величини катетів. Вихідні – величина гіпотенузи та площі трикутника. Складемо таблицю ідентифікаторів:

Таблиця 3.8. Таблиця опису величин для прикладу 3.1.

величина	ідентифікатор		тип
	вхідні величини
перший катет	a	дійсне
другий катет	b	дійсне
	вихідні величини
гіпотенуза	c	дійсне
площа	s	дійсне

Складемо математичну модель:

Складаємо алгоритм, блок-схема якого зображена на рис. 3.:

Запишемо програму:

var a, b, c, s: real;

begin

writeln(‘введіть катети трикутника a, b’);

readln(a, b);

c:=sqrt(sqr(a)+sqr(b));

s:= a*b/2;

writeln(‘гіпотенуза трикутника c=’, c);

writeln(‘площа трикутника s=’, s)

end.

Рис. 3.2 Блок-схема алгоритму до прикладу 3.1.

Приклад 3.2. Знайти площу кільця, внутрішній радіус якого дорівнює r, а зовнішній - R

(r < R).

У зв’язку з тим, що Pascal не розрізняє великі та малі літери, введемо наступні позначення:

величина	ідентифікатор	тип
	вхідні величини
внутрішній радіус	rv	дійсне
зовнішній радіус	rz	дійсне
	вихідні величини
площа	s	дійсне

Складемо математичну модель:

.

У зв’язку з тим, що лілійні алгоритми дуже прості і ви вже навчилися їх складати, надалі ми опустимо їх зображення у вигляді блок-схеми, а подамо його у вигляді програми. Як ми вже знаємо , у мові Pascal використовується наперед визначена константа PI. Запишемо програму:

var rv, rz, s: real;

begin

writeln(‘введіть радіуси кола: внутрішній та зовнішній rv, rz’);

readln(rv, rz);

s:= pi*(sqr(rz)-sqr(rv));

writeln(‘площа кола s=’, s);

readln;

end.

Приклад 3.3.Задане натуральне двозначне число. Знайти суму його цифр.

величина	ідентифікатор	тип
	вхідні величини
натуральне число	n	натуральне
	проміжні величини
перша цифра	a	натуральне
друга цифра	b	натуральне
	вихідні величини
сума цифр	s	натуральне

Складемо математичну модель:

Нехай n=23= 2*10+3;. Тоді a= n div 10=2; b=n mod 10=3;

Запишемо програму:

var n, a, b, s: byte;

begin

writeln(‘введіть натуральне двозначне число n’);

readln(n);

a:= n div 10;

b:= n mod 10;

s:= a+b;

writeln(‘сума цифр’, s);

readln;

end.