Практичне заняття №1.

Матриці та дії над ними.

1.Для матриць 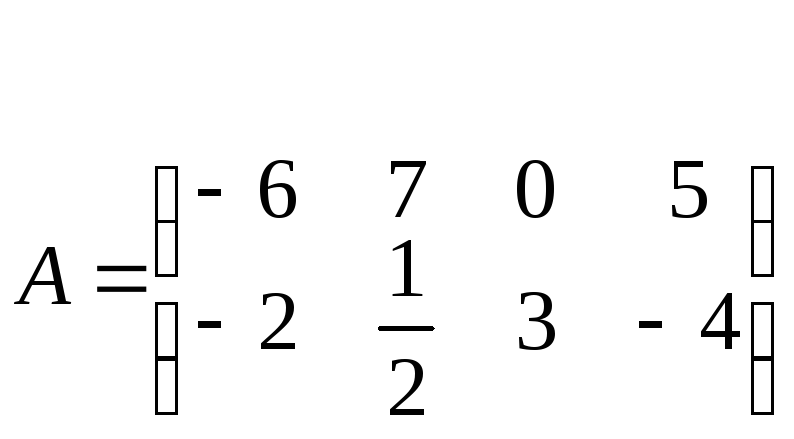та

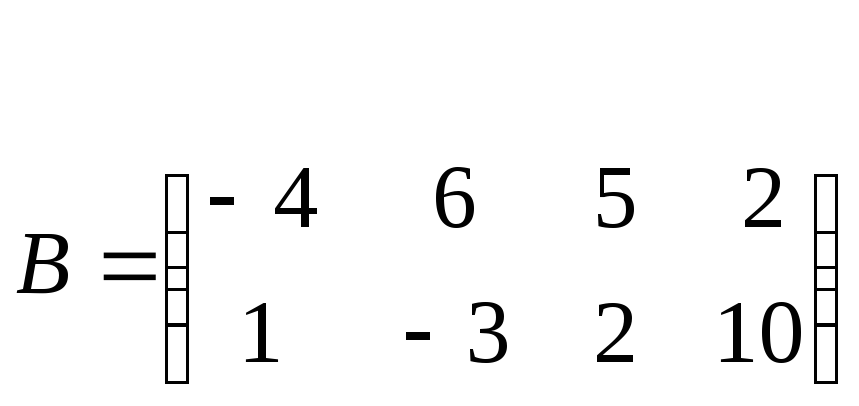
обчислити лінійні комбінації А-В, 2А+4В, 10А-1,2В.

2. Задано матриці:

, .

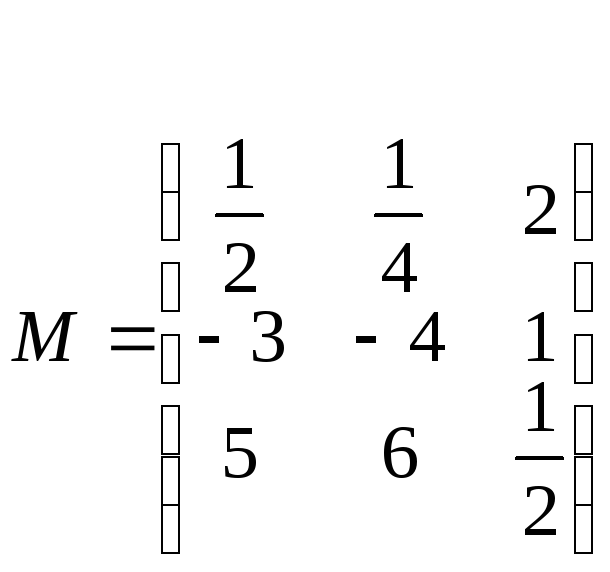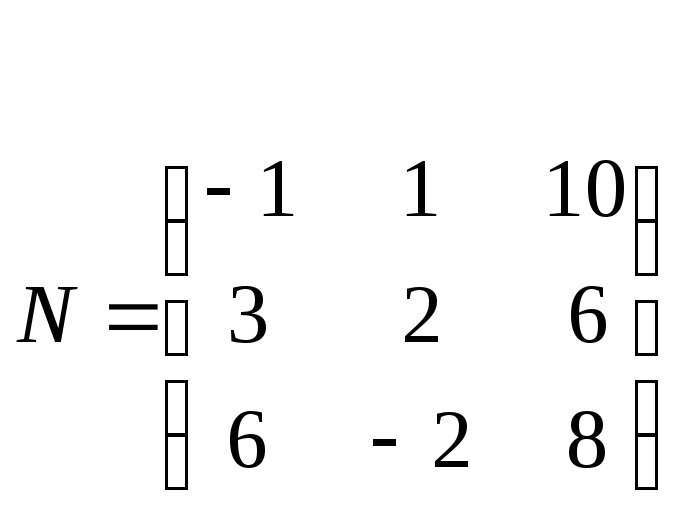Обчислити:

а) , б) , в) , г) , д) .

Практичне заняття №2.

Елементи теорії визначників. Знаходження оберненої матриці за наведеним алгоритмом. Розв’язування матричних рівнянь.

1.Обчислити визначники:

, .

2.Обчислити визначники а) по правилу трикутника;

б) розкладанням за елементами першого рядка;

в) розкладанням за елементами другого стовпчика;

г) використовуючи властивості визначників:

, , .

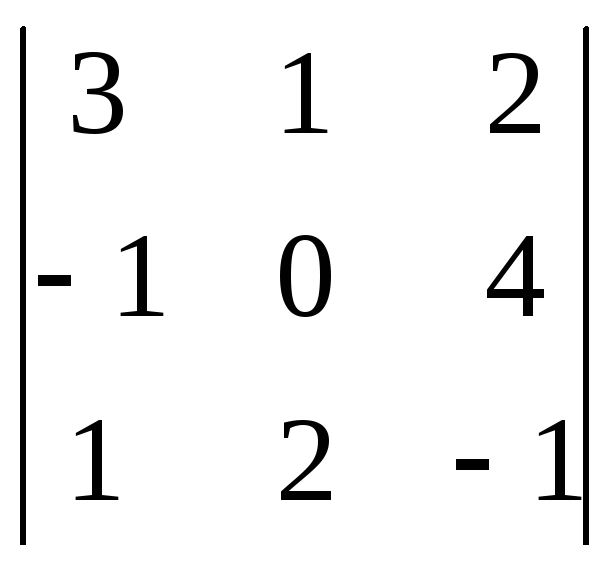3.Обчислити визначники:

, .

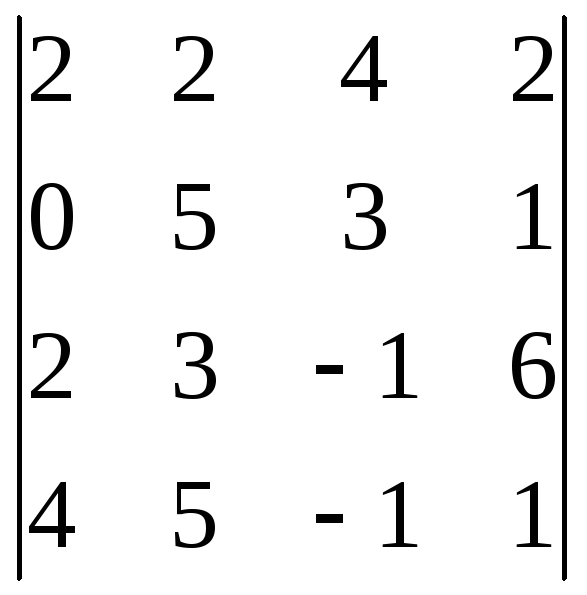4. Перевірити, чи будуть матриці А і В оберненими:

.

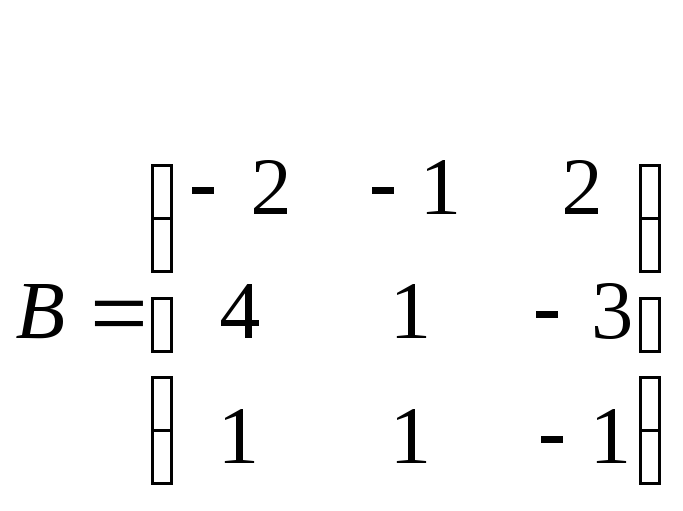5. Розв’язати матричні рівняння:

а) , б) ,

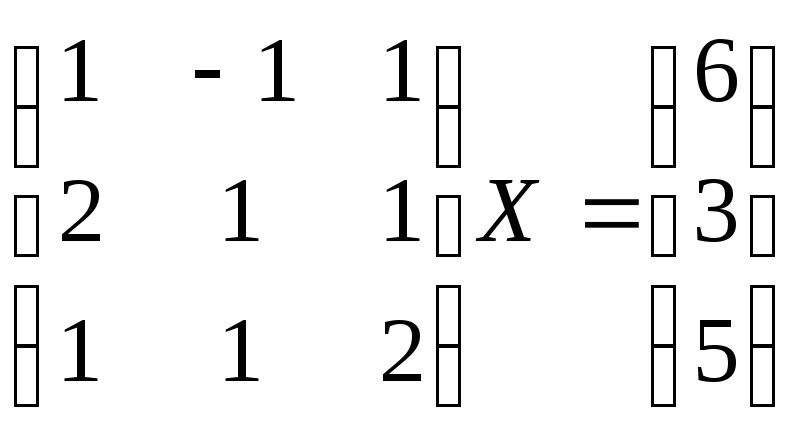в) , г) .

Практичне заняття №3.

Системи лінійних рівнянь та методи їх розв’язування.

Розв’язати системи а) методом Крамера,

б) матричним методом,

в) методом Гаусса:

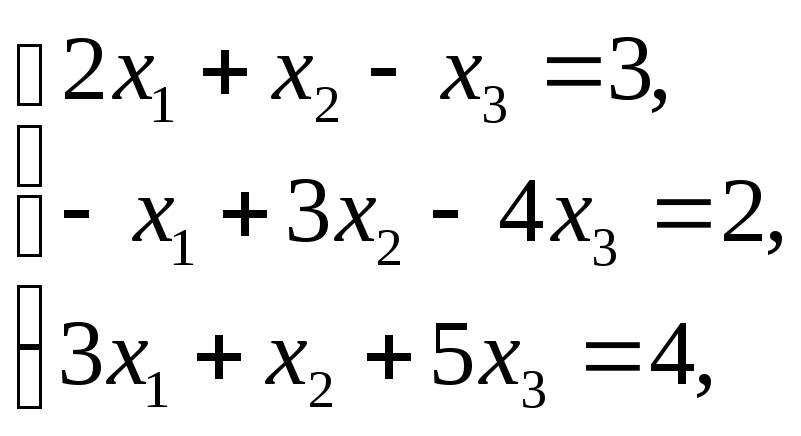
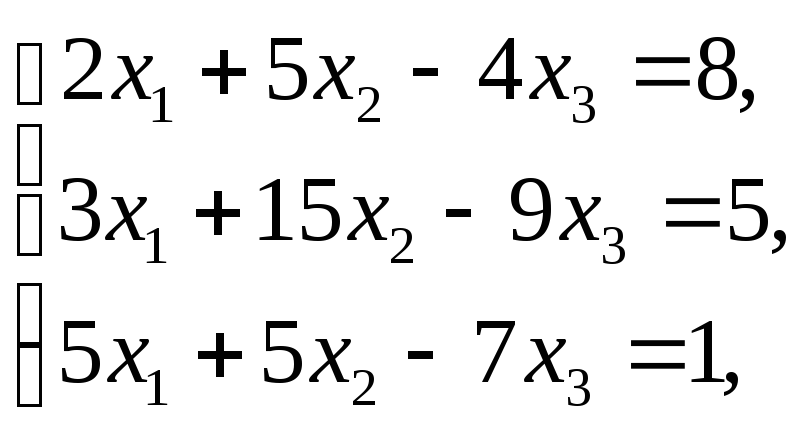
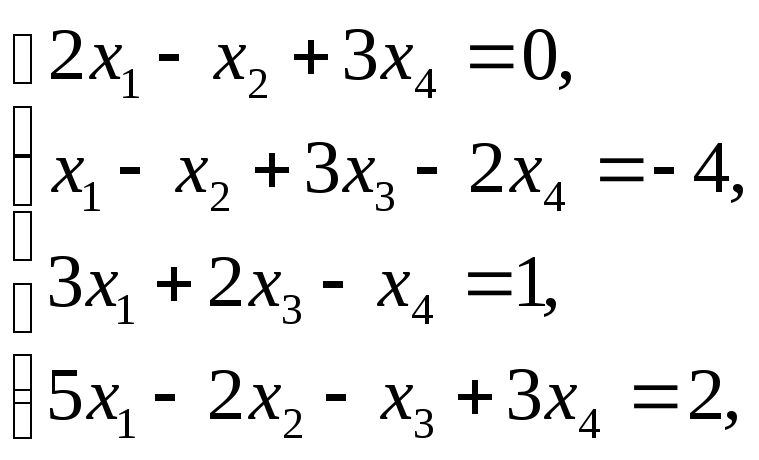
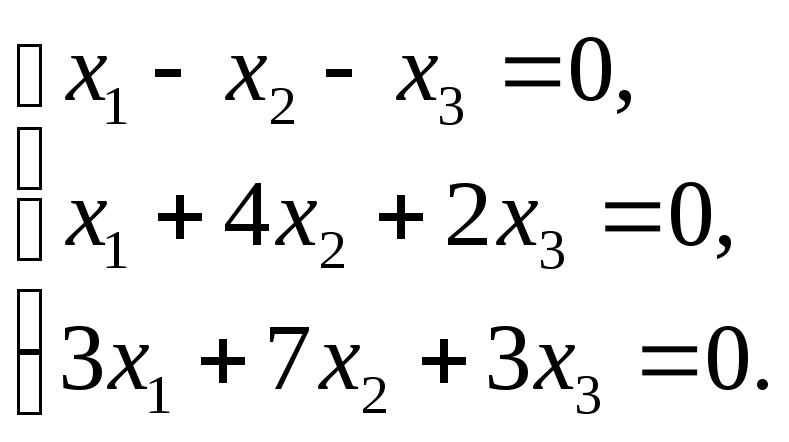
Практичне заняття №4.

Елементи векторної алгебри.

1. Задано координати точок A(2; 1; -4), В(1; 3; 5), С(7; 2; 3) та D(8; 0; -6).

Довести, що АВСD – паралелограм та знайти довжини його сторін та величини кутів.

2. В трикутнику АВС знайти довжину медіани, проведеної з вершини С, та кут між цією медіаною та сторонами СА та СВ. Знайти проекцію сторони СА на сторону СВ та проекцію сторони СВ на сторону АС.

3. Довести, що у чотирикутника АВСD діагоналі перпендикулярні, якщо координати вершин наступні: А(1; 2; 3), В(7; 3; 2), С(-3; 0; 6) та D(9; 2; 4).

4. Задано координати точок A(2; 3; 4), В(-1; 0; 6), С(-2; 2; 3) та D(-3; 3; 0).

Знайти: площу трикутника АВС та паралелограма, побудованого на векторах

;

об’єм піраміди АВСD та об’єм паралелепіпеда, побудованого на

векторах ;

висоту трикутника АВС, проведену з вершини А;

висоту піраміди АВСD, проведену з вершини D.

Практичне заняття №5.

Рівняння прямої на площині.

В трикутнику АВС задано координати вершин: A(-1; -2), В(4; -1), С(3; 5).

Скласти рівняння: а) всіх сторін трикутника;

б) всіх медіан трикутника;

в) всіх висот трикутника;

г) всіх прямих, що проведені через вершини трикутника

паралельно протилежним сторонам;

Знайти величини всіх кутів трикутника.

Практичне заняття №6.

Лінії другого порядку.

Звести лінії другого порядку до канонічного вигляду; знайти координати центрів, вершин, фокусів; побудувати.

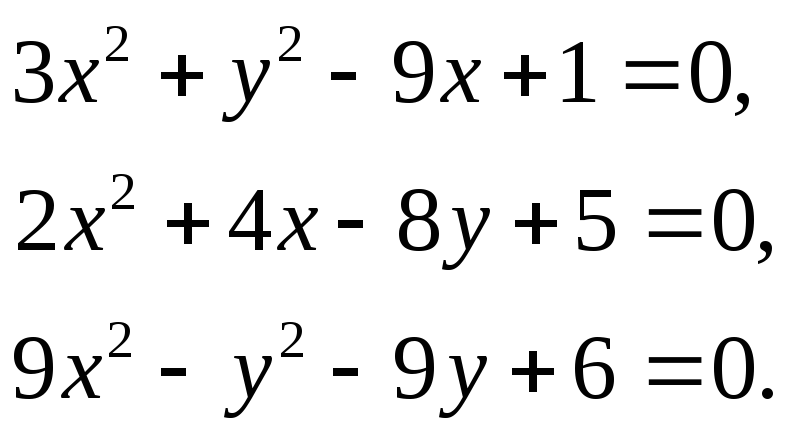
Практичне заняття №7.

Аналітична геометрія у просторі.

1) Скласти рівняння площини, що проходить через три точки .

2) Скласти рівняння площини, що проходить через точку паралельно площині .

3) Скласти рівняння площини, що проходить через точку перпендикулярно лінії перетину площин .

4) Скласти рівняння площини, що проходить через точки

перпендикулярно площині .

5) Скласти рівняння площини, що проходить через точку паралельно векторам .

6) Через точку провести пряму, яка паралельна заданій прямій р.

а) р:;

б) р: ;

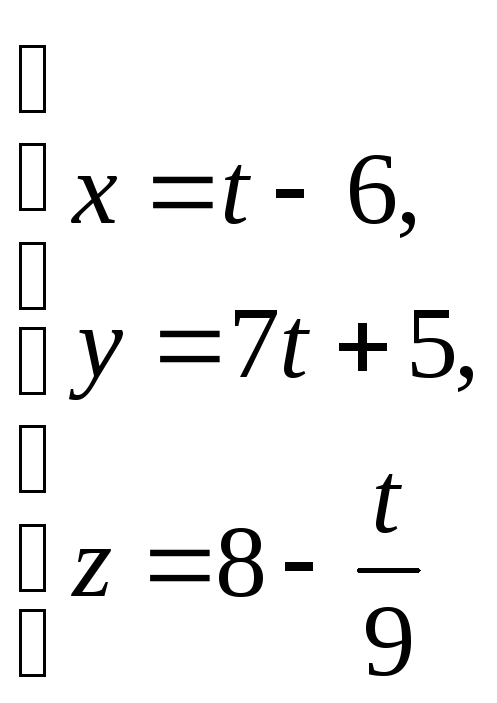в) р: ;

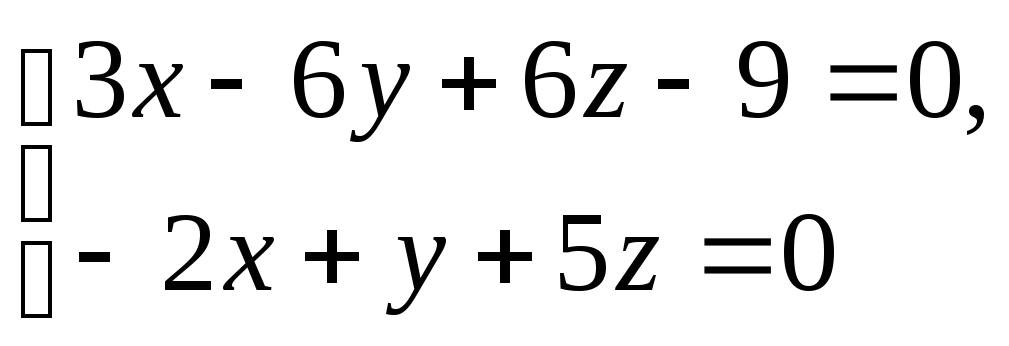7) Знайти кут між прямими та .

8) Скласти рівняння площини, що проходить через пряму

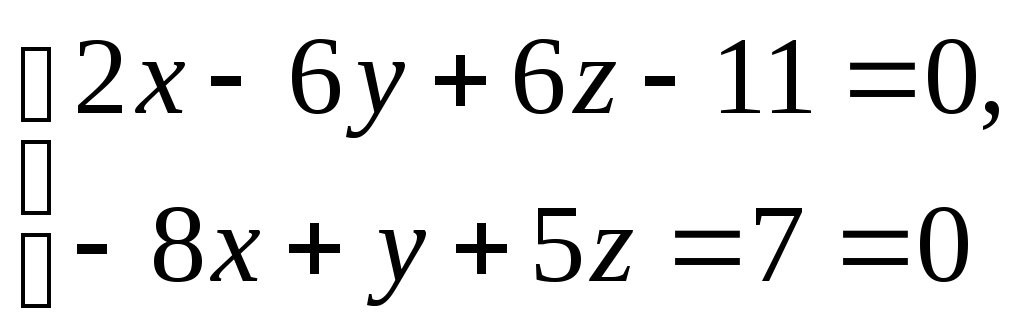
та точку .

9) Знайти відстань між точкою та площиною .

10) Знайти точку перетину площини та прямої .

Практичне заняття № 8.