5.1. Системы с неограниченной растворимостью

Рис. 6.3. Система координат для построения диаграмм двухкомпонентных систем.

компонентов в твердом и жидком состоянии.

Диаграммы этих систем бывают с точками экстремумов на линиях диаграммы (точки минимума и максимума) и без таковых. Наиболее часто в металлических системах встречаются диаграммы без максимумов и минимумов (рис. 6.4).

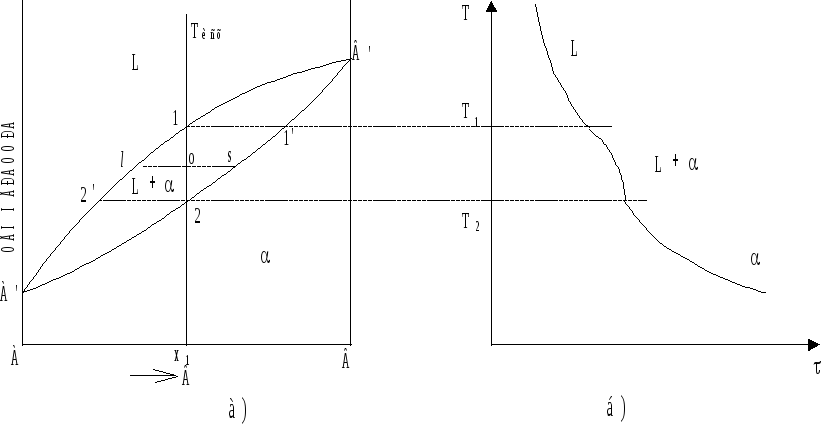
Рис. 6.4. Диаграмма состояния системы с неограниченной растворимостью компонентов (с образованием непрерывного ряда твердых растворов) (а) и кривая охлаждения сплава x₁ (б).

Диаграмма состоит из трех областей: жидкий раствор (L), твердый раствор () и область двухфазного равновесия (L +).

Сплав состава x₁ при Т_ИСХ представляет собой однородную жидкость, ненасыщенную относительно твердой фазы. Для этой температуры правило фаз дает:

с = k - f + 1 = 2 - 1 + 1 = 2,

т. е. Т и С - два независимых параметра состояния.

При температуре точки 1 начинается процесс кристаллизации сплава: жидкость насыщается относительно кристаллов - твердого раствора состава точки 1’, которые из нее и выделяются. Линия 1 - 1’, соединяющая составы равновесных фаз, называетсяконодой.

Число степеней свободы системы для точки 1:

с = k - f + 1 = 2 - 2 + 1 = 1,

т. е. Т = f (C).

Действительно, уравнение Т = f (C) это уравнение линии ликвидус.

Температурный интервал (Т₁ - Т₂) - интервал кристаллизации. Процесс кристаллизации сопровождается изменением состава равновесных фаз и может быть описан уравнением вида:

.(6.6)

Уравнение (6.6) - уравнение процесса первичной кристаллизации. Для точки 2 число степеней свободы составит:

с = k - f + 1 = 2 - 2 + 1 = 1,

т. е. Т = f (C) и определяет положение линии солидус.

Таким образом, состав первых кристаллов определяется проекцией точки 1’ на ось концентраций, а последних капель жидкости - проекцией точки 2’.

Относительные массовые доли фаз (О. М. Д.) кристаллизующегося сплава при температуре точки О определяется из соотношений (правило рычага):

, . (6.7)

Изменение температуры сплава x₁ в процессе его охлаждения изображается соответствующей кривой охлаждения (рис. 6.4), построенной в координатах “температура - время”.

5.2. Системы с неограниченной растворимостью компонентов в жидком состоянии и ограниченной в твердом.

Таких систем примерно на порядок больше, чем ранее рассмотренных.

Рис. 6.5. Диаграмма состояния системы эвтектического

типа (а) и кривая охлаждения сплава x₁ (б).

Системы эвтектического типа.

Диаграмма эвтектического типа изображена на рис. 6.5.

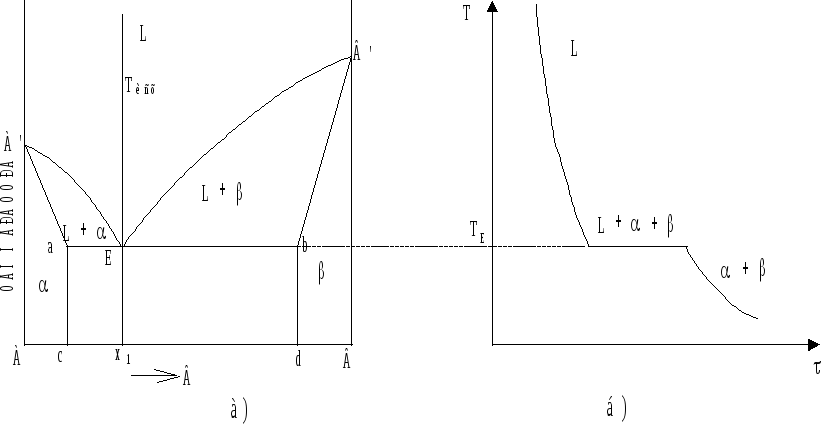
Линия A’EB’ - линия ликвидус, линия A’аEbB’ - солидус, линия аEb - эвтектическая горизонталь. Эвтектика в переводе с греческого - легкоплавящаяся.

Линии ас и bd - линии сольвус или линии предельной растворимости компонентов друг в друге.

Области и- области твердых растворов. Твердыми растворами называются однородные кристаллические фазы сплавов, у которых атомы растворяемого компонента замещают атомы растворителя в его кристаллической решетке.

При Т_ИСХ сплав состава x₁ представлен однородной жидкостью, которая по достижении температуры эвтектической горизонтали (Т_Е) насыщается одновременно по отношению к двум твердым растворам: - раствору состава точки (а) и- раствору состава точки b, которые из нее и выделяются. Происходит так называемое эвтектическое превращение, которое можно описать уравнением вида:

.(6.8)

В результате эвтектического превращения образуется эвтектическая смесь двух фаз: и. Вариантность системы при Т_Е определится:

с = k - f + 1 = 2 - 3 + 1 = 0,

т. е. нонвариантное равновесие в двухкомпонентной системе реализуется при постоянной температуре (Т_Е) и постоянных составах фаз (,).

При дальнейшем охлаждении составы равновесных фаз не изменяются.

Системы перитектического типа.

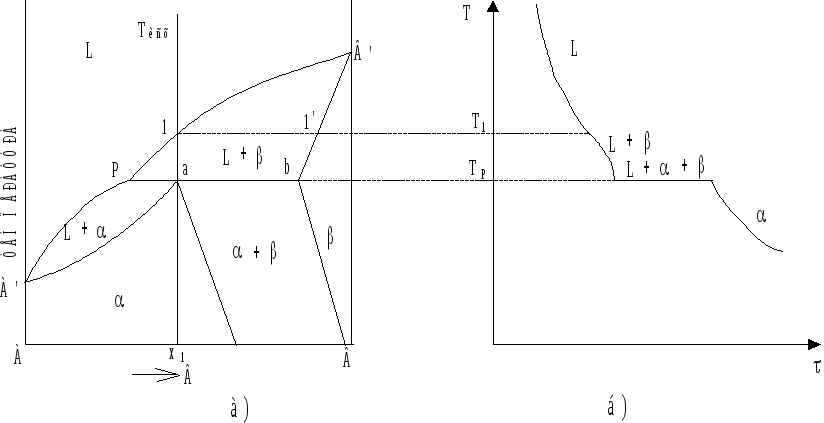
“Перитектос” - окружение (греч.). Диаграмма состояния перитектического типа изображена на рис. 6.6.

До температуры точки 1 охлаждается однородная жидкость , которая при температуре Т₁ насыщается относительно - твердого раствора, который начинает выделяться. Процесс выделения- твердого раствора продолжается в интервале температур (Т₁ - Т_Р) и может быть описан уравнением вида:

,

характеризующим процесс первичной кристаллизации.

Рис. 6.6. Диаграмма состояния системы перитектического типа (а)

и кривая охлаждения сплава x₁ (б).

.(6.9)

При температуре Т_Р (температура перитектической горизонтали Раb) жидкость состава точки Р становится ненасыщенной по отношению к выпавшим кристаллам - твердого раствора и пересыщенной по отношению к кристаллам- твердого раствора состава точки а. Поэтому- кристаллы растворяются в жидкости, а- кристаллы из нее выделяются.

Уравнение (6.9) описывает процесс перитектической кристаллизации.

Число степеней свободы для системы при Т_Р:

с = k - f + 1 = 2 - 3 + 1 = 0.

Системы с промежуточными фазами.

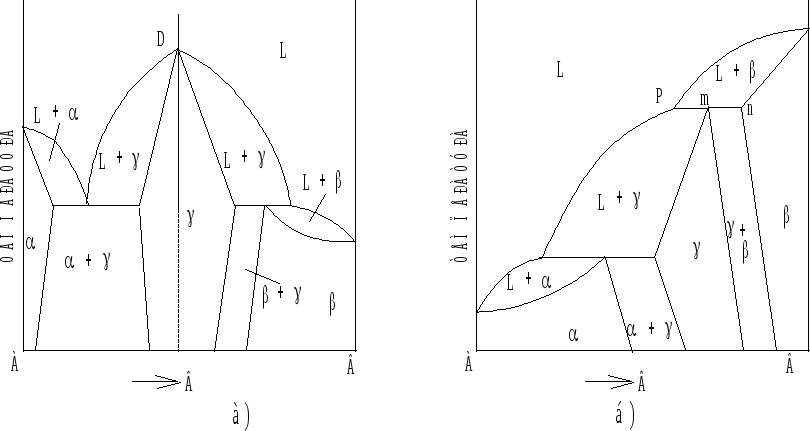
Рис. 6.7. Диаграммы состояния с конгруентно (а) и

инконгруентно (б) плавящейся промежуточной фазой.

Системы с промежуточными фазами делятся на две группы: с конгруентно (рис. 6.7, а) и с инконгруентно плавящимися промежуточными фазами (рис. 6.7, б).

Если составы жидкости и твердой фазы при температуре плавления совпадают (т. D), то такие системы называют системами с конгруентно плавящейся промежуточной фазой (рис.6.7, а), а если составы равновесных фаз при температуре плавления не совпадают (рис. 6.7, б), то это системы с инконгруентно плавящейся промежуточной фазой.

Точка D называется дистектической (трудноплавящейся) точкой.

Системы с ограниченной растворимостью в жидком состоянии.

Диаграммы состояния систем с ограниченной растворимостью в жидком состоянии представлены диаграммами двух типов: с монотектическим и синтектическим превращениями (рис. 6.8 а,б).

Линия nkm - купол расслоения - линия ограниченной растворимости в жидком состоянии.

При охлаждении сплава x₁ (рис. 6.8, а) и достижении им температуры точки 1 жидкость состава точки 1 насыщается по отношению к другой жидкости состава точки 1’. В интервале (Т₁ - Т₂) идет процесс расслоения, сопровождающийся изменением состава жидкостей:

. (6.10)

Системы синтектического типа в реальных металлургических системах встречаются редко. Смысл синтектического превращения может быть представлен схемой вида:

,(6.11)

для которого

с = k - f + 1 = 2 - 3 + 1 = 0.

Рис. 6.8. Диаграммы состояния систем с расслоением.