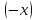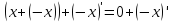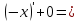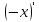1.2. Свойства линейного пространства
Непосредственно из аксиом линейного пространства можно получить ряд простейших свойств.
Свойство 1.1. Любое линейное пространство имеет только один нулевой вектор.
Доказательство: В аксиоме в) линейного пространства не утверждается, что нулевой вектор должен быть единственным. Но из аксиом а) и в) в совокупности это вытекает. Пусть существуют два нулевых вектора 0 и 0'. Тогда
|
0 = |
аксиома в) |
= 0 + 0' = |
аксиома а) |
= 0' + 0 = |
аксиома в) |
=0' |
Здесь в роли нулевого элемента сначала выступает вектор 0', а затем 0. Видим, что векторы 0 и 0' совпадают.
Свойство 1.2. Каждый вектор линейного пространства имеет только один противоположный вектор.
Доказательство:
Пусть
для вектора
 существуют
два противоположных вектора
существуют
два противоположных вектора
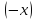 и
и
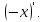 Согласно
аксиоме г) линейного пространства это
означает, что
Согласно
аксиоме г) линейного пространства это
означает, что
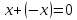 и
и
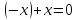 .
Рассмотрим двойную сумму
.
Рассмотрим двойную сумму
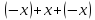 '
элементов
линейного
пространства. Согласно аксиоме б) эта
сумма не зависит от порядка выполнения
двух операций сложения. Меняя порядок
сложения, получаем:
'
элементов
линейного
пространства. Согласно аксиоме б) эта
сумма не зависит от порядка выполнения
двух операций сложения. Меняя порядок
сложения, получаем:
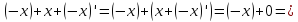
|
аксиома в) |
= |
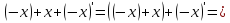
|
аксиома а) |
=
|
|
аксиома а) |
=
|
|
аксиома в) |
=
|
Свойство
1.3. Если
вектор
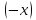 противоположен вектору
противоположен вектору
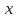 то вектор
то вектор
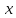 противоположен вектору
противоположен вектору
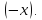
Доказательство: Утверждение опирается на коммутативность сложения. Действительно,
«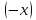 противоположен
противоположен
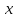 »
»  ,
,
«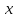 противоположен
противоположен
 »
» 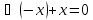 .
.
Справа стоят эквивалентные равенства (в силу аксиомы а)). Значит, и утверждения слева равносильны.
Свойство
1.4. Для
любых двух векторов
 и
и
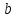 уравнение
уравнение
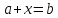 относительно
относительно
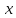 имеет решение, и притом единственное.
имеет решение, и притом единственное.
Существование:
Решением уравнения
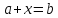 является
вектор
является
вектор
 ,
так
как
,
так
как
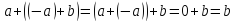 .
.
Единственность:
Пусть
 - какое-либо решение указанного уравнения,
т.е. выполнено равенство
- какое-либо решение указанного уравнения,
т.е. выполнено равенство
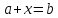 .
Прибавив
к обеим частям этого равенства вектор
.
Прибавив
к обеим частям этого равенства вектор
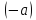 ,
получим
,
получим
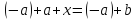 ,
откуда
,
откуда
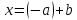 .
Видим,
что вектор
.
Видим,
что вектор
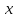 совпал
с указанным выше решением
совпал
с указанным выше решением
 .
Значит,
других решений нет.
.
Значит,
других решений нет.
Последнее
свойство позволяет ввести еще одну
операцию в линейном пространстве,
которая является противоположной
cложению.
Разностью
двух
векторов
 называют
вектор
называют
вектор
 ,
являющийся решением уравнения
,
являющийся решением уравнения
 (вспомним, что разностью двух чисел
(вспомним, что разностью двух чисел
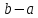 называют
такое число, которое в сумме с вычитаемым
а
дает
уменьшаемое
называют
такое число, которое в сумме с вычитаемым
а
дает
уменьшаемое
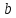 ).
Из доказательства свойства 1.4 вытекает,
что
).
Из доказательства свойства 1.4 вытекает,
что
 .
.
Свойство
1.5. Произведение
произвольного
элемента
линейного
пространства на
число
0
равно нулевому вектору:
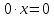
Свойство
1.6. Вектор,
противоположный данному вектору
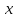 ,
равен произведению
,
равен произведению
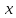 на число
на число
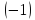 :
:
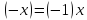 .
.
Свойство
1.7. Произведение
нулевого вектора на любое число есть
нулевой вектор:
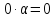 .
.
Вопросы и задачи
1.1. Может ли линейное пространство состоять из:
а) двух элементов; б) одного элемента; в) 100 элементов?
1.2. Выясните, образует ли линейное пространство:
а) множество всех векторов данной плоскости, не параллельных данной прямой, относительно линейных операций над векторами;
б) множество всех векторов плоскости с началом в начале системы координат, расположенных в правой полуплоскости, относительно обычных операций сложения и умножения векторов;
в) множество кососимметрических матриц третьего порядка относительно операции сложения матриц и умножения матрицы на число;
г) множество
функций вида
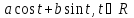 ,
относительно обычных операций сложения
функций и умножения функции на число;
,
относительно обычных операций сложения
функций и умножения функции на число;
д) множество многочленов степени п относительно обычных операций сложения многочленов и умножения многочлена на число.
1.3.
Пусть
множество М
состоит
из одного элемента
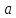 .
Определим операции сложения и умножения
на действительное число
.
Определим операции сложения и умножения
на действительное число
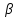 соответственно
равенствами:
соответственно
равенствами:
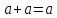 и
и
 Является ли М
линейным
пространством?
Является ли М
линейным
пространством?
1.4.
Предположим,
что множество М
состоит
из всевозможных упорядоченных пар
действительных чисел
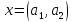 .
Пусть на этом множестве заданы следующие
операции: а) если
.
Пусть на этом множестве заданы следующие
операции: а) если
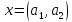 ,
,
 ,
то
,
то
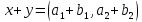 ;
б) если
;
б) если
 и
и
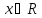 ,
то
,
то
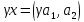 .
Является ли М линейным пространством?
.
Является ли М линейным пространством?
1.5.
Является
ли линейным пространством множество
всех действительных чисел, если операции
сложения ⊕
и умножения ⊙
на
число ввести следующим образом:
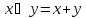 ,
,
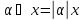 ?
?
1.6. Докажите, что множество матриц-столбцов высоты п образует линейное пространство относительно матричных операций сложения и умножения.