
MU_gi_2014
.pdf
Задание №2
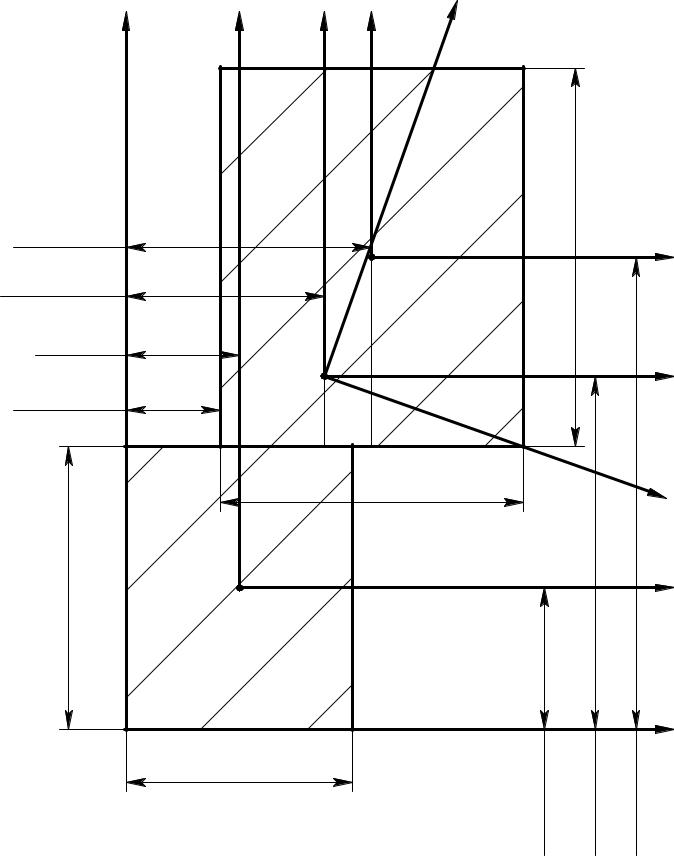
Дано: h1= 7.5 см; b1= 6 см; h2= 10 см; b2= 8 см; z0= 2.5 см.
1. Определим площади простых сечений
А1 = h1·b1 = 7.5 ·6 = 45 см2
А2 = h2·b2 = 10 ·8 = 80 см2
2. Определим координаты центра тяжести каждой из простых фигур
z1 = b21 = 62 = 3 см
z2 = z0 + b22 = 2.5 + 82 = 6.5 см
y1 = h21 = 72.5 = 3.75 см
y2 = h1 + h22 = 7.5 + 102 = 12.5 см
3. Определяем координаты центра тяжести фигуры
z |
C |
= |
A1·z1 |
+ A2·z2 |
= |
45 |
· 3 + 80 |
· 6.5 |
= 5.24 см |
||
A1 |
+ A2 |
|
45 + |
80 |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
y |
C |
= |
A1·y1 |
+ A2·y2 |
= |
45 |
· 3.75 |
+ |
80 · 12.5 |
= 9.35 см |
|
|
|
|
|
|
|
||||||
|
|
A1 |
+ A2 |
|
|
45 |
+ |
80 |
|
|
|
|
|
|
|
|
|
|
|||||
4. Определяем моменты инерции простых фигур состовляющих сечение
Jz1 = b112· h13 = 6 ·127.53 = 210.938 см4
Jz2 = b212· h23 = 8 ·12103 = 666.667 см4
Jy1 = b1312· h1 = 63 12· 7.5 = 135 см4
Jy2 = b2312· h2 = 8312· 10 = 426.667 см4
5. Найдем растояние между центральными осями всего сечения и центральными осями простых фигур
а1 = y1 - yC = 3.75 - 9.35 = -5.6 см
а2 = y2 - yC = 12.5 - 9.35 = 3.15 см
c1 = z1 - zC = 3 - 5.24 = -2.24 см
c2 = z2 - zC = 6.5 - 5.24 = 1.26 см
Y |
Y1 |
Yc Y2 |
V |
|
|
|
|
|
|
|
|||
z2=6.5cм |
|
|
|
h2=10cм |
|
Z2 |
|
|
c2 |
|
|
||
zc=5.24cм |
|
|
|
|
||
|
|
|
|
|
||
z1=3cм |
|
|
|
|
|
|
z0=2.5cм |
|
C |
|
|
|
Zc |
|
|
|
|
|
||
|
|
|
b2=8cм |
|
|
U |
h1=7.5cм |
|
|
|
|
|
|
c1 |
|
|
|
|
Z1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y1=3.75см |
yc=9.35cм |
y2=12.5cм |
Z |
|
b1=6см |
|
|
|||
|
|
|
|
6. Найдем моменты инерции простых фигур относительно центральных осей всего сечения
JzcI = Jz1 + а12 ·· A1 = 210.938 + (-5.6)2 · 45 = 1622.137 см4
JzcII = Jz2 + а22 ·· A2 = 666.667 + (3.15)2 · 80 = 1460.467 см4
JycI = Jy1 + c12 ·· A1 = 135 + (-2.24)2 · 45 = 360.792 см4
JycII = Jy2 + c22 ·· A2 = 426.667 + (1.26)2 · 80 = 553.675 см4
JzcycI = Jz1y1 + a1 ··c1 · A1 = 0 + (-5.6) · (-2.24) · 45 = 564.48 см4
JzcycII = Jz2y2 + a2 ··c2 · A2 = 0 + (3.15) · (1.26) · 80 = 317.52 см4
7. Найдем центральные моменты инерции всей фигуры
J |
zc |
= J |
I + J |
II |
= 1622.137 + 1460.467 = 3082.6 см4 |
||||||||
|
|
|
zc |
zc |
|
|
|
|
|||||
J |
yc |
= J |
I + J |
II |
= 360.792 + 553.675 = 914.47 см4 |
||||||||
|
|
|
yc |
yc |
|
|
|
|
|||||
J |
zcyc |
= J |
I + J |
|
II = 564.48 + 317.52 = 882 см4 |
||||||||
|
|
|
|
zcyc |
|
|
|
zcyc |
|
||||
8. Найдем главные моменты инерции |
|
||||||||||||
J |
max |
= |
|
Jzc + Jyc |
|
+ |
1 |
(Jzc - Jyc)2 + 4·Jzcyc2 |
= |
||||
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||
3082.6 + 914.47 + |
1 |
|
(3082.6 - 914.47)2 + 4·(882)2 = 3396.076 см4 |
||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||
J |
min |
= |
Jzc + Jyc |
|
- |
1 |
(Jzc - Jyc)2 + 4·Jzcyc2 |
= |
|||||
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||
3082.6 + 914.47 - |
1 |
|
|
(3082.6 - 914.47)2 + 4·(882)2 = 600.994 см4 |
|||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
9. Найдем положение главных осей
tan(αmax) = Jzcyc = 882 = -0.355 Jyc - Jmax 914.47 - 3396.076
αmax = -19.566 |
|
|
||||
tan(α |
|
) = |
Jzcyc |
= |
882 |
= 2.814 |
min |
|
914.47 - 600.994 |
||||
|
|
Jyc - Jmin |
|
|||
αmin = 70.434
Задание № 3 Плоский изгиб прямых брусьев.
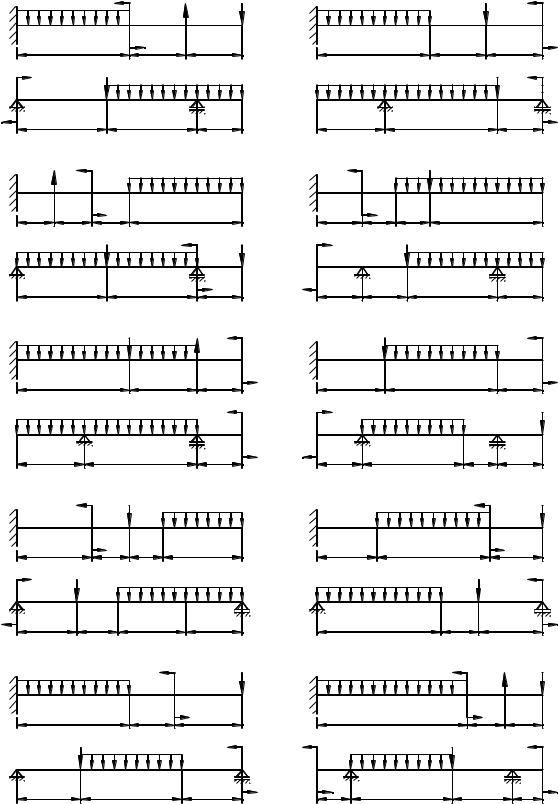
Для заданных двух расчетных схем балок (рис. 3) требуется написать выражения для поперечных сил Q и изгибающего момента
M для каждого участка в общем виде, построить эпюры Q и M ,
найти Mmax и подобрать:
а) для схемы а деревянную балку круглого и прямоугольного поперечного сечения при =10 МПа;
б) для схемы б стальную балку двутаврового поперечного сечения при =160 МПа.
Для подобранных сечений построить эпюру . Исходные данные взять в таблице 3
Таблица 3
№ п/п |
Схема |
|
a, м |
|
P , кН |
|
q , кН/м |
M , кНм |
|
|
|
|
|
|
|
|
|
0 |
|
9 |
|
1 |
|
20 |
3 |
18 |
1 |
|
5 |
|
1 |
|
14 |
3 |
18 |
2 |
|
7 |
|
1 |
|
10 |
3 |
24 |
3 |
|
7 |
|
3 |
|
20 |
3 |
10 |
4 |
|
9 |
|
2 |
|
16 |
2 |
14 |
5 |
|
8 |
|
1 |
|
10 |
2 |
18 |
6 |
|
8 |
|
2 |
|
10 |
3 |
12 |
7 |
|
3 |
|
2 |
|
16 |
3 |
26 |
8 |
|
3 |
|
1 |
|
16 |
5 |
12 |
9 |
|
9 |
|
2 |
|
14 |
4 |
18 |
10 |
|
7 |
|
2 |
|
14 |
2 |
14 |
11 |
|
6 |
|
2 |
|
20 |
3 |
14 |
12 |
|
10 |
|
2 |
|
10 |
3 |
20 |
13 |
|
5 |
|
2 |
|
20 |
3 |
24 |
14 |
|
4 |
|
2 |
|
14 |
2 |
12 |
15 |
|
9 |
|
1 |
|
12 |
3 |
14 |
16 |
|
7 |
|
2 |
|
16 |
3 |
26 |
17 |
|
10 |
|
1 |
|
16 |
3 |
20 |
18 |
|
6 |
|
1 |
|
10 |
4 |
12 |
19 |
|
7 |
|
1 |
|
14 |
3 |
24 |
№ п/п |
Схема |
|
a, м |
|
P , кН |
|
q , кН/м |
M , кНм |
|
|
|
|
|
|
|
|
|
20 |
|
4 |
|
1 |
|
18 |
3 |
22 |
21 |
|
2 |
|
3 |
|
18 |
2 |
16 |
22 |
|
8 |
|
1 |
|
18 |
3 |
10 |
23 |
|
9 |
|
2 |
|
14 |
4 |
10 |
24 |
|
2 |
|
3 |
|
18 |
3 |
16 |
25 |
|
4 |
|
3 |
|
18 |
4 |
22 |
26 |
|
8 |
|
3 |
|
16 |
3 |
26 |
27 |
|
6 |
|
3 |
|
12 |
3 |
14 |
28 |
|
5 |
|
2 |
|
12 |
4 |
10 |
29 |
|
9 |
|
2 |
|
16 |
2 |
24 |
30 |
|
3 |
|
3 |
|
12 |
3 |
18 |
31 |
|
1 |
|
2 |
|
18 |
2 |
20 |
32 |
|
6 |
|
2 |
|
18 |
4 |
10 |
33 |
|
4 |
|
1 |
|
14 |
3 |
20 |
34 |
|
4 |
|
2 |
|
18 |
3 |
22 |
35 |
|
9 |
|
2 |
|
18 |
2 |
20 |
36 |
|
8 |
|
2 |
|
18 |
5 |
16 |
37 |
|
1 |
|
2 |
|
12 |
3 |
10 |
38 |
|
8 |
|
2 |
|
12 |
2 |
18 |
39 |
|
5 |
|
2 |
|
12 |
3 |
22 |
40 |
|
5 |
|
2 |
|
14 |
4 |
22 |
41 |
|
1 |
|
3 |
|
18 |
4 |
20 |
42 |
|
2 |
|
1 |
|
12 |
4 |
12 |
43 |
|
9 |
|
2 |
|
18 |
3 |
20 |
44 |
|
8 |
|
3 |
|
14 |
4 |
24 |
45 |
|
4 |
|
3 |
|
12 |
3 |
12 |
46 |
|
6 |
|
1 |
|
10 |
2 |
22 |
47 |
|
5 |
|
3 |
|
14 |
4 |
18 |
48 |
|
3 |
|
3 |
|
14 |
4 |
26 |
49 |
|
5 |
|
2 |
|
16 |
2 |
26 |
50 |
|
2 |
|
2 |
|
16 |
4 |
16 |
51 |
|
8 |
|
3 |
|
18 |
3 |
12 |
52 |
|
8 |
|
3 |
|
12 |
2 |
14 |
53 |
|
2 |
|
1 |
|
12 |
4 |
24 |
54 |
|
5 |
|
3 |
|
18 |
4 |
14 |
55 |
|
9 |
|
2 |
|
20 |
3 |
24 |
56 |
|
10 |
|
2 |
|
18 |
4 |
26 |
57 |
|
3 |
|
2 |
|
16 |
3 |
16 |
2
№ п/п |
Схема |
|
a, м |
|
P , кН |
|
q , кН/м |
M , кНм |
|
|
|
|
|
|
|
|
|
58 |
|
5 |
|
2 |
|
10 |
5 |
26 |
59 |
|
6 |
|
2 |
|
18 |
3 |
24 |
60 |
|
6 |
|
2 |
|
12 |
2 |
14 |
61 |
|
9 |
|
1 |
|
16 |
5 |
26 |
62 |
|
3 |
|
2 |
|
16 |
2 |
18 |
63 |
|
6 |
|
2 |
|
14 |
3 |
18 |
64 |
|
6 |
|
2 |
|
10 |
4 |
18 |
65 |
|
3 |
|
2 |
|
12 |
5 |
26 |
66 |
|
4 |
|
3 |
|
14 |
4 |
18 |
67 |
|
6 |
|
1 |
|
16 |
3 |
12 |
68 |
|
4 |
|
2 |
|
12 |
4 |
12 |
69 |
|
3 |
|
1 |
|
18 |
3 |
16 |
70 |
|
9 |
|
2 |
|
16 |
4 |
10 |
71 |
|
3 |
|
1 |
|
12 |
2 |
20 |
72 |
|
3 |
|
3 |
|
20 |
5 |
22 |
73 |
|
7 |
|
2 |
|
18 |
5 |
16 |
74 |
|
5 |
|
3 |
|
16 |
3 |
24 |
75 |
|
8 |
|
2 |
|
12 |
2 |
22 |
76 |
|
3 |
|
3 |
|
14 |
3 |
14 |
77 |
|
6 |
|
3 |
|
14 |
3 |
16 |
78 |
|
9 |
|
2 |
|
18 |
2 |
26 |
79 |
|
5 |
|
3 |
|
12 |
3 |
14 |
80 |
|
4 |
|
3 |
|
18 |
3 |
26 |
81 |
|
3 |
|
3 |
|
14 |
2 |
20 |
82 |
|
7 |
|
3 |
|
16 |
5 |
14 |
83 |
|
5 |
|
3 |
|
18 |
2 |
22 |
84 |
|
2 |
|
3 |
|
16 |
5 |
24 |
85 |
|
5 |
|
3 |
|
20 |
2 |
26 |
86 |
|
2 |
|
2 |
|
10 |
4 |
20 |
87 |
|
8 |
|
1 |
|
10 |
5 |
14 |
88 |
|
9 |
|
2 |
|
18 |
3 |
10 |
89 |
|
5 |
|
1 |
|
16 |
2 |
20 |
90 |
|
10 |
|
2 |
|
16 |
2 |
22 |
91 |
|
5 |
|
2 |
|
12 |
5 |
16 |
92 |
|
4 |
|
2 |
|
12 |
2 |
10 |
93 |
|
9 |
|
3 |
|
18 |
4 |
22 |
94 |
|
2 |
|
1 |
|
20 |
4 |
22 |
95 |
|
6 |
|
2 |
|
14 |
4 |
16 |
3
№ п/п |
Схема |
|
a, м |
|
P , кН |
|
q , кН/м |
M , кНм |
|
|
|
|
|
|
|
|
|
96 |
|
4 |
|
1 |
|
12 |
3 |
16 |
97 |
|
4 |
|
1 |
|
10 |
2 |
18 |
98 |
|
5 |
|
3 |
|
12 |
3 |
16 |
99 |
|
2 |
|
1 |
|
12 |
3 |
24 |
Порядок расчета
I.Находим реакции опор (только для схемы б). II. Разбиваем схему на участки.
III. Составляем выражения для Q и М на каждом из участков. IV. Строим эпюры Q и М (в масштабе).
V. Определяем размеры поперечного сечения балки из условия прочности по нормальным напряжениям.
4
I а) |
|
q |
|
M |
P P II а) |
|
q |
|
|
P |
|
M |
||
|
|
|
|
|
|
|
|
|||||||
|
|
2a |
|
a |
|
a |
|
|
3a |
|
a |
|
a |
|
б) |
M |
|
P |
q |
|
б) |
|
|
q |
|
|
P |
M |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2a |
|
2a |
|
a |
|
2a |
|
|
4a |
|
3a |
|
IIIа) |
P |
|
M |
|
q |
|
IVа) |
|
M |
P |
|
q |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a |
a |
a |
|
4a |
|
|
1.5a |
a |
a |
|
3a |
|
|
б) |
|
q P |
|
|
M P б) M |
P |
|
q |
|
|
||||
|
|
4a |
|
4a |
|
a |
|
a |
a |
|
4a |
|
a |
|
V а) |
|
q |
P |
|
P |
M |
VIа) |
|
P |
|
q |
|
|
M |
|
3a |
|
2a |
|
a |
2a |
|
4a |
|
a |
||||
|
|
|
|
|
|
|
|
|||||||
б) |
|
|
q |
|
|
M |
б) |
M |
|
q |
|
|
P |
|
|
|
|
|
|
|
|
|
|
||||||
|
2a |
|
4a |
|
a |
|
a |
|
4a |
|
a |
2a |
|
|
VII |
|
|
M |
P |
q |
|
VIII |
|
|
|
q |
M |
P |
|
|
|
|
а) |
|
|
|
||||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
a |
a |
2a |
|
2a |
|
4a |
|
2a |
|
||
б) |
M P |
|
q |
|
б) |
|
q |
|
P |
|
M |
|||
|
|
|
|
|
|
|
|
|||||||
|
2a |
a |
2a |
|
2a |
|
|
4a |
|
a |
|
2a |
|
|
IX |
|
q |
|
|
M |
P |
X а) |
|
|
q |
|
M |
P |
P |
а) |
|
|
|
|
|
|
|
|
||||||
|
|
3a |
|
a |
2a |
|
|
6a |
|
a |
a |
|
||
б) |
|
P |
q |
|
|
M |
б) M |
|
q |
P |
|
M |
||
2a |
4a |
|
|
4a |
a |
|||||||||
|
|
2a |
|
a |
|
|
2a |
|
||||||
Рисунок 3 Расчетные схемы. |
|
|
|
|
|
|
|
|
||||||
5
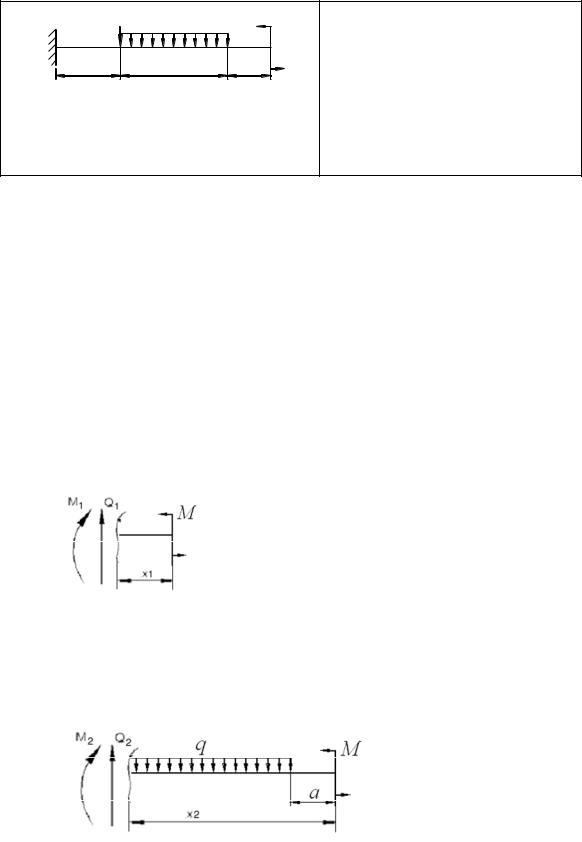
Пример решения 3а
VI |
P |
q |
|
q= 3 кН/м; |
а) |
|
M |
M =8 кНм; |
|
|
2a |
4a |
a |
P=6 кН; |
|
|
|
|
а = 3м; |
|
|
|
|
h/b= 2; |
|
|
|
|
[ ]= 10 МПа. |
Определить: размеры прямоугольного и круглого поперечного сечения.
Решение
I. Разбиваем схему на участки.
Разбиваем заданную схему на участки. Наша расчетная схема состоит из 3 участков: первый – АВ; второй – ВС и третий – CD.
II. Составляем выражения для Q и М на каждом из участков.
Определяем значения Q и M на границах участков и в характерных точках.
Участок I 0 х1 a 3м
Q1(х1) = 0.
М1(х1) М 8кНм;
Участок II а 3м х2 5а 15м
6
Q2(х2) q x2 а ;
Q2(x2 3м) 3 (3 3) 0кН; Q2(x2 15м) 3 (15 36) 0кН
М2(х2) q (x2 2)2 M ; 2
М2(х2 3м) 3 (3 3)2 8 8кНм; 2
М2(х2 9м) 3 (9 3)2 8 46кНм; 2
М2(х2 15м) 3 (15 3)2 8 208кНм 2
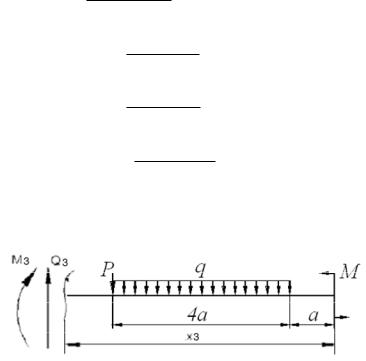
Участок III 5а 15м х3 7а 21м;
Q3(х3) q 4a Р 3 12 6 42кН
М3(х3) q (x3 3a) 4a Р (х3 5а) M ;
М3(х3 15м) 3 (15 9) 12 6 (15 15) 8 208кНм
М3(х3 21м) 3 (21 9) 12 6 (21 15) 8 460кНм
III.Строим эпюры Q и М (в масштабе).
По полученным данным строим эпюры Q и M
7
