Лабораторна робота №7 Криптоаналіз шифру Віженера з періодичним ключем

1. Теоретичні відомості.

Нехай – скінчена група. Розглянемо шифросистему. Інформація представляється послідовністю. Сеансовий ключ – (потенційно нескінчена) періодична послідовність– «гамма», тобто накладається на інформацію, що генерується, за допомогою порозрядної групової операції. Таким чином, шифротекст має вид

,

де . Такий шифр називають іноді шифром Віженера (або шифром Вернама).

Криптоаналіз шифросистеми може бути здійснений у відповідності до такої схеми, що складається з двох етапів: на 1-у етапі обчислюється періодсеансового ключа, а на 2-у етапі – сам сеансовий ключ.

1-й етап (тобто обчислення періоду сеансового ключа) здійснюється у відповідності дометоду Ф. Казіскі (1863р.):

Два однакових відрізка відкритого тексту, що відстоять один від одного на відстані , зашифровані однаково.

Індексом збігу в послідовності називається ймовірність того, що збігаються два випадково обраних елементи цієї послідовності. Цей індекс обчислюється у відповідності до формули:

,

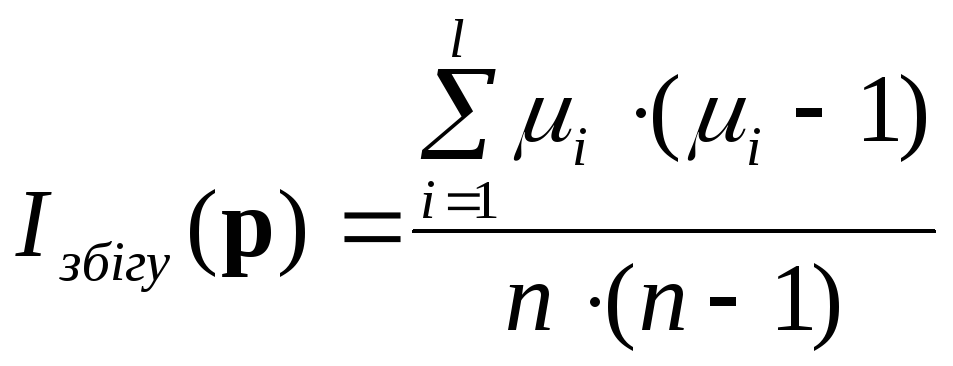де – число входжень елементув послідовність.

Нехай – ймовірність появи елементув осмисленому тексті. Тоді

для будь-якого осмисленого тексту .

За допомогою цієї формули можуть бути підраховані індекси збігу в осмисленому тексті для будь-якої природної мови. Для деяких європейських мов такі індекси наведені в таблиці 8.1.

Таблиця 7.1

Мова	Російська	Англ.	Франц.	Нім.	Італ.	Іспан.
	0.0529	0.0662	0.0778	0.0762	0.0738	0.0775

Обчислення періоду сеансового ключаздійснюється в такий спосіб. Представимо шифротекств виді матриці

.

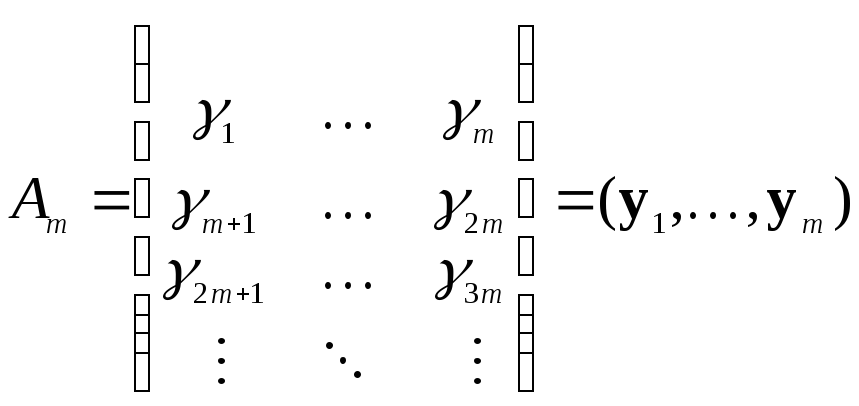Якщо , то для кожного стовпцяматриці

,

оскільки кожний стовпець матриці– це результат застосуванняфіксованої циклічної перестановки , визначеної на множині .

Якщо ж , то

,

де – індекс збігу у випадковому тексті природної мови, яка використовується.

Оскільки для будь-якої природної мови , то обчислення періодусеансового ключане складає особливих зусиль.

2-й етап (тобто обчислення сеансового ключа при відомому його періоді ) здійснюється в такий спосіб.

Взаємним індексом збігу в послідовностях іназивається ймовірність того, що випадково обраний елемент послідовностізбігається з випадково обраним елементом послідовності. Взаємний індекс збігу в послідовностяхіобчислюється у відповідності до формули:

,

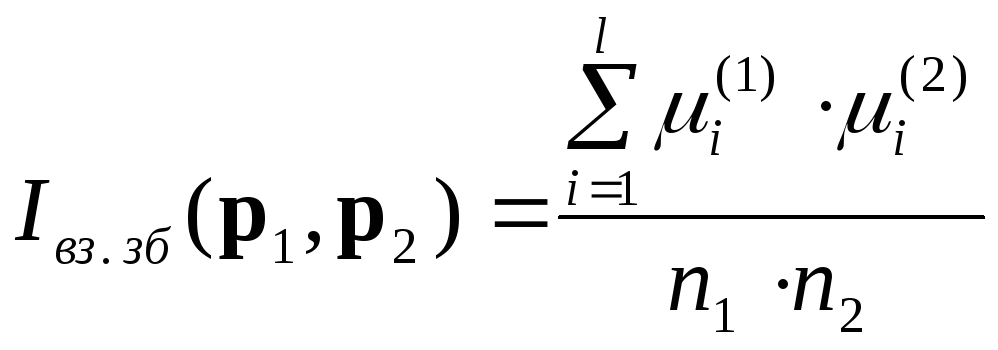де – число входжень елементув послідовність. Оскільки періодсеансового ключавідомий, то відома матриця

,

де кожний стовпець отриманий в результаті застосуванняфіксованої циклічної перестановки , що визначена на множині.

Розглянемо аналіз матриці , якщо, дедля всіх. Кожна циклічна перестановкамає вид

,

тобто представляє собою відносний зсув на величину . Звідси витікає, що

,

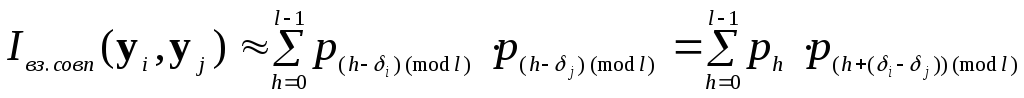де – ймовірність появи елементув відкритому тексті. А оскільки

,

то стовпці із відносними зсувами на величиниімають однакові взаємні індекси збігу. По аналогії з індексами збігу, взаємні індекси збігу при зсуві на величинуможуть бути обчислені для будь-якої природної мови.

Нехай – стовпець, який отримано в результаті додавання (по модулю) елементадо кожного елемента стовпця. За допомогою формули

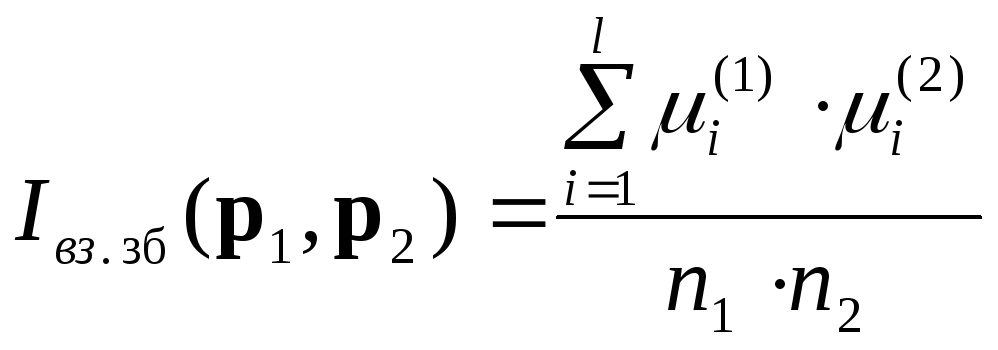
можуть бути обчислені значень. Якщо, тоблизько до взаємного індексу збігу при зсуві на величинудля природної мови, що використовується, а якщо, тоістотно відрізняється від цього індексу, тобто обчислення сеансового ключа зводиться до пошуку розв’язків системи лінійних рівнянь

.

2. Завдання на проведення лабораторної роботи.

Для шифротексту (файл «…Задания ЛР07\CText*.txt», де * − номер варіанту) визначити період сеансового ключа (1-й етап криптоаналізу) та відновити ключ (2-й етап).