
- •Механические и реоло ические модели оснований и фундаментов
- •1. Модели грунтовых оснований
- •1.3.1. Фундаментальные уравнения теории упругости
- •1.3.2. Перемещения и деформации
- •1. Различные определения линейной деформации
- •1.3.3. Расчёт деформаций основания
- •1.7. Фильтрационные модели (фильтрационная консолидация слоя грунта)
- •2. Модели бетона, железобетона, фундаментов зданий и сооружений
1.3.1. Фундаментальные уравнения теории упругости
Среди пространственных задач теории упругости наибольшее значение имеют задачи Буссинеска (Boussinesq, 1885), Р. Миндлина (Mindlin, 1950) и К. Кельвина (Kelvin). Область, занятая упругой сре-дой, – полупространство0£ z .
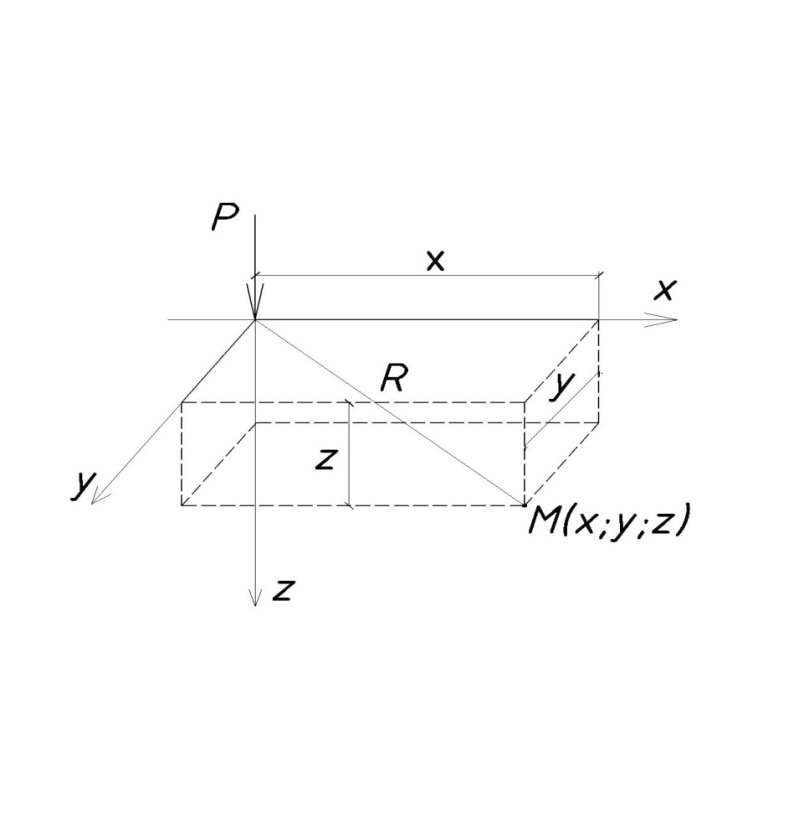
Задача Буссинеска [8, 32]. Граница области – горизонтальная плоскость z = 0 – везде свободна от напряжений, кроме начала коор-динат, в котором приложена сосредоточенная вертикальная сила R (рис. 1).
Решение задачи даётся формулами:
3P
x2z (1-
2v) 1 (
R
+
z)x2 z
х 2p
R5
3
R(R
+
z)
(R
+
z
2
R3
R3
3P
y2z (1-
2v) 1 2R
+
z)y2 z
y 2p
R5
3
R(R
+
z)
(R
+
z
2
R3
R3
3P
z3 P 3 1 P
z 2p
R5
z2
2p
1+
r
2
5/2
z2
sz
=
1
nKiP, txz
=
3P
xz2;
i=1
tyz
=
3P
yz2,
K
=
3 1 ;
2
1
z
2
t
=
3P
xyz
-
(1-
2v)
2R
+
z
xy
,
R R z R
где
R=
x2
+
y2
+z2
.
12
M(0;
0;
0)
M(x; y; z)
Рис. 1. Схема к задаче Буссинеска
Перемещения, параллельные осям координат:
u
=
P
xz
-
1-
2n) x ;
4pG R3 R(R + z)
v
=
4pG
yz-
(1-
2n)
R(R
+
z);
w
=
4pG
z2+21-
n)R
.
На основе решения задачи Буссинеска путём интегрирования мо-гут быть получены решения задач для полупространства при действии произвольной вертикальной нагрузки, распределённой по некоторой площади на поверхности полупространства. Некоторые решения этой задачи приводятся в [8].
Аналогом задачи Буссинеска является задача о сосредоточенной касательной силе, приложенной к поверхности полупространства. Не-которые формулы этой задачи приводятся в [8]. Посредством суперпо-зиции решений данной задачи и задачи Буссинеска можно получить решение для произвольной наклонной нагрузки на поверхность полу-пространства.
Возможность применения рассмотренных выше решений для опре-деления напряжений в грунтовых основаниях основывается на прибли-жённой аппроксимации связи между напряжениями и деформациями линейными соотношениями закона Гука, что справедливо для некоторо-го диапазона допредельных напряжённых состояний. Отсюда следует,
13
что данные решения тем лучше будут соответствовать реальному рас-пределению напряжений в грунте, чем меньшее развитие получили в основании области предельного равновесия и тем более течения.
Так как законы деформирования грунта для нагрузки и разгрузки неодинаковы, то следует избегать применения решений теории упру-гости без учёта последовательности изменения силовых факторов, т.е. без учёта истории нагружения основания.
Наконец, следует отказаться от формального использования ре-шений теории упругости в случаях, когда решением предсказываются значительные растягивающие напряжения в грунте, поскольку в дей-ствительности грунт практически не способен сопротивляться растя-жению.
Задача Р. Миндлина [8, 32]. Сила Р приложена внутри упругого полупространства на расстоянии с от поверхности основания (рис. 2).
Решение задачи даётся следующими формулами. Перемещение в радиальном направлении:
P´r z
-
c (3-
4u)(z
-
c) 4(1-
u)(1-
2u) 6cz(z
+c)
16pG(1-
u)
R
3
R23
R2(R2
+
z
+
c)
R25
где
G
=
E
(1+
u)
–
модуль
сдвига;
2
R
=
(z-c)2
+r2;
R
=
(z+c)2
+r2
.

Плоскость
Z=0 (0;0;-c)

X
(0;0;+c)
2
R1
r
Y (x;y;z)
Z
Рис. 2. Схема к задаче Р. Миндлина для вертикальной силы, приложенной внутри упругого полупространства
14
Перемещение в вертикальном направлении:
P 3-
4u 8(1-
u)2
-(3-
4u) (z
-c)2
16pG(1-
u)
R
R2
R
3
+
(3-
4u)(z
+c)2
-
2cz
+
6cz(z
+c)2
;
R R
sx=
8 (P
u)(1-2
)(z-c)
-
3x2(z-c)
+
(1-2
)[3(z-c)-4
(z+c)]-
-
3(3-4
)x2(z-c)-6c(z+c)[(1-2
)z-2
c]-
30cx
z(z+c)
-R R
4(1
u)(1-2
)
x2 x2
R
(R
+z+c
R
(R
+z+c R22
s
= P (1-
2u)(z
-
c)
-
3y2(z
-c)
+
(1-
2u)[3(z
-
c)-
4u(z
+c)]-8p(1-
u) R R R
-
3(3-
4u)y2(z
-c)-6c(z
+c)[(1-
2u)z
-
2uc]
-
30cy2z(z
+c)
-R R
-
4(1-
u)(1-
2u)
1- y2 -
y2
;
R
(R
+
z
+c)
R
(R
+
z
+c)
R2
s
= P -
(1-
2u)(z
-
c)
-
(1-
2u)(z
-
c)
-
3(z
-
c)3
-
8p(1-
u)
R
3 R23 R
5
-
3(3-
4u)z(z
+
c)2
-
3
(5z
-
c)
-
30cz(z
+
c)3
;
R25R27
t = Py -
(1-
2u)
+
(1-
2u)
-
3(z
-
c)2
-
8p(1-
u)
R
3 R23 R
5
-
3(3-
4u)z(z
+
c)
-
3
(3z
+
c)
-
30cz(z
+
c)2
;
R25R27
15
t
= Px -
(1-
2u)
+
(1-
2u)
-
3(z
-
c)2-
8p(1-
u)
R
3 R23 R
5
-
3(3-
4u)z(z
+
c)
-
3c(3z
+
c)
-
30cz(z
+
c)2
.
R25R27
Решение задачи даётся формулами:
u = P 3- 4u + 1 + x2 + (3- 4u)x2 + 2cz 1- 3x2 +
16pG(1-
u)
R R R R R
R
+
4(1-
u)(1-
2
)
- x2 ;
R
+
z
+c
R
(R
+
z+c)
Pxy
1 (3-4u) 6
z 4(1-
u)(1-2u)
16pG(1-
u)R3 R
3 R
5 R
(R
+z+c)2
(33)
(34)
Px z-c (3-4u)(z-c cz
z+c) 4(1-
u)(1-
u)
1
pG
1-
u)
R3
23
25
R
(R
+z+c)
Плоскость
Z=0 (0;0;-c)

X
(0;0;+c)
P
2 R1
r
Y (x;y;z)
Z
Рис. 3. Схема к задаче Р. Миндлина для горизонтальной силы, приложенной внутри упругого полупространства
16
Px
1-2 (1-2
)(5-4
)
3x2 3(3-4
)x2
x 8p(1-
u)
1
23 1
25
- 4(1
u)(1-2
)
3-x2(
R2
+z+c
c
3 -(3-2 )(z+ )+5x2
;
R
(R z
c
R
(R2
z
c)
R
R
sy= Py 1-2u
+
(1-2
)(5-4
)
-
3
5-
3(3-4
)y2
-1 2 1 2
-
4(1-
u)(1-
2
)
-
y2(
R2+
z+c)
+
6
c-(1-
u)(z+c)+
5y2z
;
R
(R
+
z+c)2
R
(R2+
z+c) 2
R
Pz 1-
2u 1-
2u 3(z
-
c2) 3(3-
4u)(z
+
c)2
z
3
3
5
5
1 2 1 2
+
6c
c
+
(1-
2u)(z
+c)
+
5z(z
2c)2;
2 2
t
=
Pxy 3(z
-
c)
-
3(3-
4u)(z
+c)
+
c
1-
2u
+
5z(z
+c)
;
p(1-
u)
R R R
R
t
= P -
(1-2
)(z-c)
+
(1-
2
)(z
-c)
-
3x2(z-c)
-8
(1-
u) R R R
-
3(3-
u)x2(z
+c)
-
-
c
z(z+c
-(1-
u)x2
-
5x2z(z
+c)
;
R R
R
t
y=
8pPy
u)-1-2u
+1-2u
-
3x2
-
3(3-4u)x2
-
4(
-
u)(1-2u)x2
x2(
R
+z+c)
cz 5x2
R
(R
+z+c)2
R
2(R
+z+c)2
R
5
R
5
17
Задача Л. Кельвина [32]. Сила приложена на значительной глу-бине ( z Ò ), когда её влияние на деформацию граничной плоскости (z = 0) незначительно.
Решение задачи даётся следующими формулами. Перемещения в направлении оси х:
u
= P(l
+
m) xz
.
8pm(l +2m) r3
Перемещения в направлении оси y:
u
= P(l
+
m) yz.
8pm(l +2m) r3
Вертикальные перемещения:
P(
+
m)
z2 l
+3
1
8pm(l
+2m)
r3
l
+
m
r
В горизонтальной плоскости приложения нагрузки осадки опре-деляются формулой:
(3-
4u)(1+
u)
8p(1-
u)r
Напряжения определяются формулами:
sr = P/8p(1- u)(1- 2u)z(r2 + z2) -3/2 -3r2z(r2 + z2) -5/2 ;
sQ = P/8p(1- u)(1- 2u)z(r2 + z2) -3/ 2;
sz
=
P/8p(1-
u)(1
2u)z(r2
+
z2)
-3/2
-3z(r2
+
z2)
-5/2
;
srz
=
P/8p(1-
u)(1-2u)r(r2
+z2)
-3/2
-3rz
(r2
+z2)
-5/2].
В формулах l и m – постоянные Ляме;
l E /(1 u)(1 2u); m = E/2(1+ u).
Решение Р. Миндлина применяют для расчёта свай (Н.М. Дорош-кевич, А.А. Бартоломей и др.), фундаментов мелкого заложения (М.И. Горбунов-Посадов, Р.С. Шеляпин, В.В. Леденев и др.). Однако по фундаментальному решению упругая среда одинаково сопротивля-ется сжатию и растяжению. Грунт на растяжение практически не рабо-
18
тает.
Вследствие
этого
за
силой
должны
возникать
разрывы
сплошно-сти
(для
реальных
грунтовых
оснований).
Предлагаются [7, 8] приближённые методы снижения растяги-вающих напряжений, например, введением двойных сил [7, 8] или принятие их равным нулю.
Плоские задачи теории упругости. Задача Фламана [8, 32]. Относится к числу статических задач теории упругости. Областью, занятой упругой средой, в данной задаче является полупространство 0 z ¥ (рис. 4). Граница области z = 0 свободна от напряжений везде, за исключением оси у, вдоль которой приложена линейная нагрузка
равномерной интенсивности R.
Рассматриваемая задача принадлежит к классу задач плоской де-формации. Это обусловлено структурой области и граничных условий: очевидно, что все плоскости, перпендикулярные оси у, являются в данной задаче равноправными, поэтому все искомые функции не зави-сят от координаты у.
Следовательно, достаточно рассмотреть только одну из таких плоскостей, например плоскость XOZ. Также очевидно, что компонен-та n вектора смещения вдоль оси у тождественно равна нулю, однако нормальное напряжение sy отлично от нуля. Из сказанного следует, что вектор смещения в задачах этого класса равен
S
=ui
+wk,
а из соотношений Коши – что тензор деформации имеет вид
e
Э = 0
1
2
xz
0
0
0
1 20xz .
ez



P
О M(x;y;z) X
Y Z
Рис. 4. Схема к задаче Фламана
19
Из
формул
закона
Гука
в
этом
случае
вытекает,
что
только
одно
касательное
напряжение
не
равно
нулю:
p
=
0
txz
0 s y
0
txz .
s z
Решение задачи:
s
=
2P x2z ;
x2 + z2
s
=
2P z3;
x2
+
z2
s
y
=
v
sX sZ
);
2P xz2
xz p
x2
+
z2
2
В реальных ситуациях грунтовое основание нередко вполне обос-нованно может рассматриваться как полупространство, однако внеш-ние нагрузки, как правило, только в немногих случаях и с большой степенью условности могут быть сведены к линейной.
Из этого не следует, однако, практическая бесполезность задачи Фламана. Решения задачи Фламана могут быть легко обобщены на случай полосовой нагрузки, для которого приводится ряд важных ин-женерных задач.
