
Л2 Надежность ИС
.pdfФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Пермская государственная сельскохозяйственная академия имени академика Д.Н.Прянишникова»
Факультет прикладной информатики Кафедра ИТАП
НАДЕЖНОСТЬ ИНФОРМАЦИОННЫХ СИСТЕМ
специальность 230201 «Информационные системы и технологии»
ЛАБОРАТОРНАЯ РАБОТА №2
тема: «РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ»
(различные законы распределения времени работы до отказа)
Структура:
1.Сведения из теории
2.Постановка задачи
3.Последовательность решения
4.Задание для самостоятельного решения
Пермь, 2011

I.СВЕДЕНИЯ ИЗ ТЕОРИИ
Вбольшинстве случаев решение вопросов, связанных с обеспечением надежно-
сти, предполагает качественное и количественное изучение объектов исследования. Ис-
следование в каждом конкретном случае специфики объектов на качественном уровне по-
зволяет установить основные критерии отказов, причины их возникновения, пути повы-
шения надежности и т.д. Решение этих задач невозможно без использования теории веро-
ятностей, математической статистики, методов оптимизации. В частности, приемы и ме-
тоды количественного анализа дают возможность исследовать функции распределения вероятностей случайных величин и оценки их основных моментов и квантилей, проведе-
ния структурного анализа и моделирования систем и процессов. В теории надежности ис-
пользуются следующие законы распределения времени работы до отказа объекта (систе-
мы): Вейбулла, гамма-распределение, Релея, экспоненциальный, усеченный нормальный,
нормальный, равномерный. В предложенной работе рассматривается лишь часть законов,
для определения которых приняты следующие обозначения:
W – Вейбулла;
Г – гамма;
R – Рэлея;
Exp – экспоненциальный.
Распределения Вейбулла и гамма-распределение являются двухпараметрическими
(имеют два параметра распределения).
Математическое ожидание и среднее квадратическое отклонение имеют следую-
щую взаимосвязь с параметрами распределений:
Таблица 1. Связь параметров распределений с математическим ожиданием и средним квадратическим отклонением
|
Распределение |
|
|
|
m |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Экспоненциальное |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
Exp( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Гамма Г( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рэлея R( ) |
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||
|
|
|
|
4 |
|
|
|
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Вейбулла W( , ) |
|
Г(1 1/ ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Г(1 2/ ) Г2 (1 1/ ) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В таблице принято |
следующее обозначение: |
|
|
|
|
|
|
|
|
|
|
|
||||||
Гамма-функция - Г( ) x 1e xdx.
0
2
Для вычисления вероятности безотказной работы и плотности распределения времени до отказа элементов используют аналитические выражения, приведенные в таблице 2.
Таблица 2. Некоторые законы распределения вероятностей
Распределение |
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
P(t) |
|
|||||
Экспоненциальное |
|
|
|
|
|
e- t |
|
|
|
|
|
|
|
e- t |
|
|||||||
Exp( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Гамма Г( , ) |
|
|
|
|
t |
1 |
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
1 I , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рэлея R( ) |
2 |
|
te |
- t2 |
|
|
e t2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вейбулла W( , ) |
|
t |
1 |
( |
t |
) |
|
|
|
t |
|
|
||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
В гамма-распределении функция |
I( ,t) |
x 1e xdx есть неполная гамма- |
||||||||||||||||||||
( ) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функция*.
II. ПОСТАНОВКА ЗАДАЧИ
Нерезервированная система состоит из 4 элементов. Элементы имеют различные законы распределения времени работы до отказа. Виды законов распределения приведены в таблице 3. В скобках указаны параметры распределений.
Таблица 3. Законы распределения времени до отказа
№ элемента |
1 |
2 |
3 |
4 |
Закон распределения времени до |
W (2;1800) |
Г (7;300) |
R (8*10-8) |
Exp (0,0002) |
отказа |
|
|
|
|
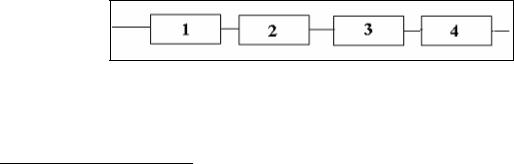
Элементы в данной нерезервированной невосстанавливаемой системе имеют последовательное (основное) соединение (рис.1).
Рис. 1. Нерезервированная система, состоящая из 4 элементов
споследовательным соединением.
*В Excel неполная гамма-функция реализуется следующий образом: в ячейку А1 помещают первый аргумент (значение ), в ячейку А2 – второй аргумент (значение t), в ячейку А3 – функция:
А3=ГАММАРАСП(А2; А1;1;1). Результатом является значение неполной гамма-функции.
3
Необходимо определить среднее время безотказной работы, среднее квадратиче-
ское отклонение времени безотказной работы, вероятность безотказной работы, для каж-
дого элемента и всей системы за время 2000 часов с шагом 100 часов. Для показателей,
зависящих от времени, решение получить в виде таблиц и графиков.
III. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ
Решение поставленной задачи рекомендуется производить с помощью электрон-
ных таблиц Microsoft Excel.
Этапы нахождения показателей надежности для данной системы:
1.Создать новый лист Microsoft Excel.
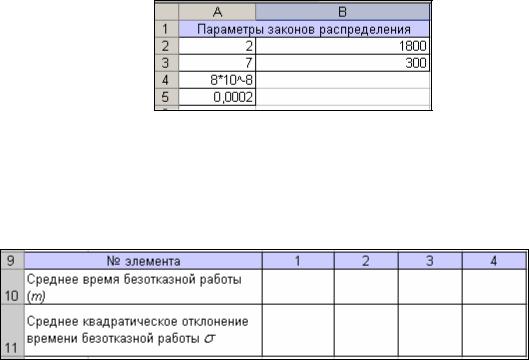
2.Необходимо создать область для ввода параметров законов распределения.
Вячейки А2:В5 вносятся параметры законов распределения времени до отказа (из усло-
вия задачи). Результат представлен на рис.1.
Рис.2. Область для ввода параметров законов распределения.
3. Далее вычисляются начальные моменты распределений: математическое ожидание m среднее квадратическое отклонение . В диапазоне ячеек А9:Е11 создать область для вычисления моментов распределения (рис.2).
Рис. 2. Область для вычисления моментов распределения.
4.Для вычисления среднего времени безотказной работы и среднего квадрати-
ческого отклонения необходимо использовать формулы связи моментов (m и ) с пара-
метрами распределений (формулы связи приведены в табл.1).
Элемент №1. Распределение Вейбулла с параметром формы 2 и парамет-
ром масштаба 1800: для вычисления математического ожидания в случае распреде-
ления Вейбулла необходимо знать и значение гамма-функции. Найти значение гамма-
функции в Excel можно по следующей технологии: в ячейке А2 находится аргумент (па- 4
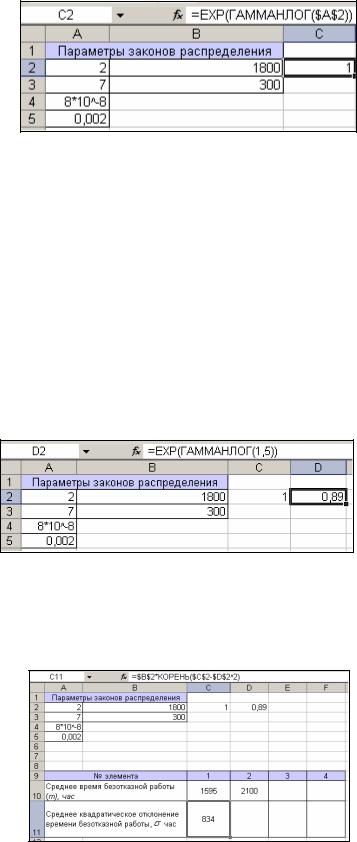
раметр формы), а в ячейку С2 необходимо поместить функцию
ЕХР(ГАММАНЛОГ(А2)), результатом является значение гамма-функции (рис.3).
Рис.3. Вычисление значения гамма-функции.
Учитывая формулу для нахождения математического ожидания (табл.1) -
Г(1 1/ ), в ячейку С10 необходимо ввести: =$B$2*EXP(ГАММАНЛОГ(1+1/$A$2)).
Для нахождения значения среднего квадратического отклонения времени без-
отказной работы необходимо знать значение гамма-функции с параметром, равным
(1+1/ ) и (1 2/ ) (табл.1). Значение гамма-функции с параметром (1 2/ ) уже извест-
но – в ячейке С2 (так как 1+2/2=2). Значение гамма-функции с параметром (1+1/ ) вы-
числяется по следующему принципу: в ячейку D2 ввести формулу
ЕХР(ГАММАНЛОГ(1,5)). Аргумент равен 1,5 исходя из условия: 1+1/2. Результат на
рис. 4.
Рис. 4. Значение гамма-функции с параметром (1 2/ ).
Теперь возможно найти . Для этого необходимо в ячейку С11 ввести формулу
=$B$2*КОРЕНЬ($C$2-$D$2^2). Результат представлен на рис.5.
Рис. 5. Результат нахождения .
5
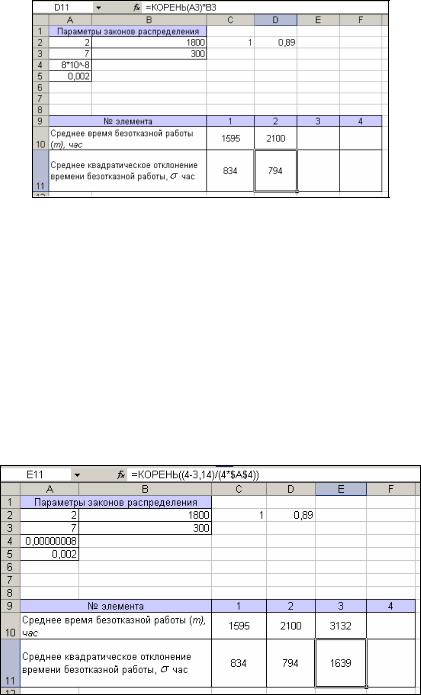
Элемент №2. Гамма-распределение с параметром формы 7 и параметром
масштаба 300: согласно формуле для нахождения математического ожидания в гамма-распределении (табл.1) в ячейку D10 ввести =A3*B3 (так как m=7*300). Для нахождения используем формулу из таблицы 1, вводя ее в ячейку D11. Результат на рис.6:
Рис.6. Вычисление среднего квадратического отклонения времени безотказной работы
Элемент №3. Распределение Рэлея с параметром 8*10 8 : для расчета матожидания значение параметра лучше вычислить заранее. Для этого в ячейку А4 перед данными параметра ставиться знак = и нажимается Enter. Значение параметра приняло вид
0,00000008.
Согласно описанным в таблице 1 формулам для m и , в ячейку E10 помещаем выражение =КОРЕНЬ(3,14/(4*$A$4)), в ячейку E11 =КОРЕНЬ((4-3,14)/(4*$A$4)). Результат представлен на рис.7:
Рис. 7. Вычисление m и для элемента №3.
Элемент №4. Экспоненциальное распределение с параметром 0,0002: при
экспоненциальном законе m= . Для ячеек F10, F11 имеет смысл =1/$A$5. Результат
представлен на рис.8:
6
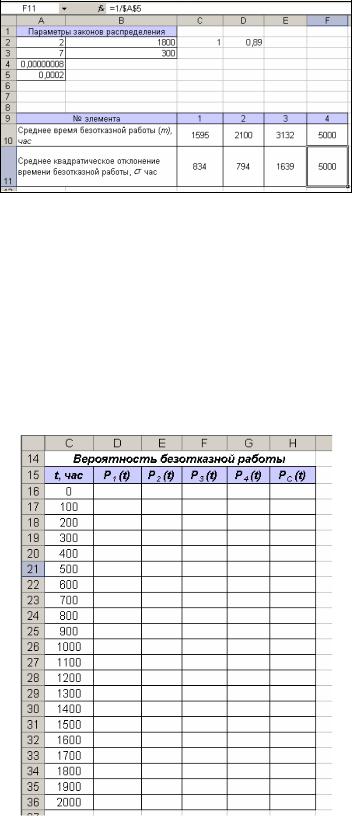
Рис. 8. Вычисление m и для элемента №4.
Таким образом, были найдены среднее время безотказной работы и среднее квадратическое отклонение времени безотказной работы для всех элементов данной системы
5.Для вычисления вероятности безотказной работы и плотности распреде-
ления времени до отказа элементов потребуются аналитические выражения, приведенные в таблице 2.
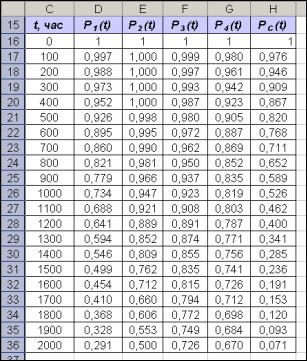
Создается область для вычисления вероятности безотказной работы элементов и системы в диапазоне ячеек C15:Н36, время – 2000 ч., шаг – 100 ч. (рис.9).
Рис. 9. Область для вычисления вероятности безотказной работы.
6. Используя формулы, приведенные в таблице 2, и подставляя значения параметров, получаем вероятности безотказной работы для элементов:
Элемент №1. Распределение Вейбулла:
7
|
t |
2 |
|
|
|
|
P1(t) e 1800 таким образом, для ячейки D16 необходима следующая формула =
=EXP(-(СТЕПЕНЬ(C16/$B$2;2))).
Элемент №2. Гамма-распределение:
|
|
|
t |
|
|
|
P2 |
(t) 1 I |
7, |
|
|
, таким образом, для ячейки E16 необходима следующая фор- |
|
300 |
||||||
|
|
|
|
|
мула =1-ГАММАРАСП(C16/$B$3;$A$3;1;1).
Элемент №3. Распределение Рэлея:
P3(t) e 8*10 8t2 , таким образом, формула для ячейки F16 имеет вид =EXP(- $A$4*(СТЕПЕНЬ(C16;2))).
Элемент №4. Экспоненциальное распределение:
P4(t) e 0,0002t, таким образом, формула для ячейки G16 =EXP(-$A$5*C16).
Необходимо табулировать эти функции от 0 до 2000 часов с шагом 100 часов.
7.Самостоятельно вычислите вероятность безотказной работы для всей систе-
мы. Сравните полученный результат со значениями, приведенными на рис.10.
Рис.10. Вероятность безотказной работы каждого элемента и всей системы за время 2000 ч., с интервалом 100 ч.
8.По полученным данным постройте графики функций, соответствующие ве-
роятностям безотказной работы элементов (рис.11) и вероятности безотказной работы
8
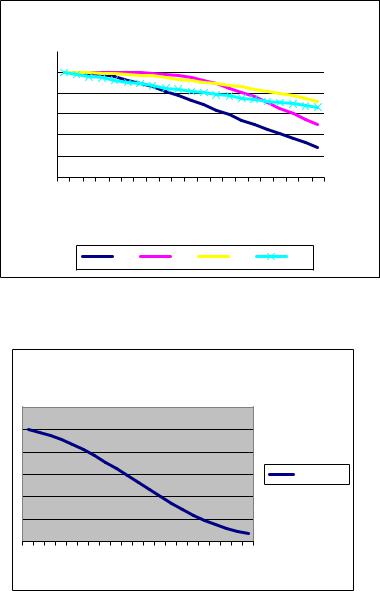
системы (рис.12). По первому графику проследите различное поведение вероятностей безотказной работы элементов. Какие элементы оказываются наиболее надежными при большом времени работы?
|
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙРАБОТЫ |
|
||||||
|
|
|
|
ЭЛЕМЕНТОВ |
|
|
||
|
|
|
|
|
|
|
|
Э3 |
P(t) |
|
|
|
|
|
|
|
Э4 |
|
|
|
|
|
|
|
Э2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Э1 |
0 |
200 |
400 |
600 |
800 |
1000 1200 |
1400 1600 1800 2000 |
t, час |
|
|
|
|||||||
|
|
|
Э1 |
|
Э2 |
Э3 |
Э4 |
|
Рис.11. График вероятностей безотказной работы элементов. |
||||||||
|
|
ВЕРОЯТНОСТЬБЕЗОТКАЗНОЙРАБОТЫ |
||||||||
|
|
|
|
|
|
СИСТЕМЫ |
|
|
||
|
|
|
|
|
|
|
|
|
|
Система |
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
Рис. 12. График вероятности безотказной работы системы. |
||||||||||
IV. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Самостоятельное определение плотность распределения времени до отказа, ин-
тенсивность отказов каждого элемента. Решение необходимо получить в виде таблиц и графиков.
9
