13. Треугольник Паскаля

Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений.

Значения 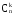представлены в табл. 6, которая называется треугольником Паскаля.

Таблица 6

Треугольник Паскаля

k n	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1
8	1	8	28	56	70	56	28	8	1

Заметим, что .

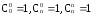Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности. Его можно представить несколько иначе – в виде [26]: равнобедренного треугольника (рис. 10).

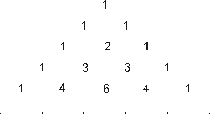
Рис. 10. Треугольник Паскаля

Здесь каждое число, кроме единиц на боковых сторонах, является суммой двух чисел, стоящих над ним. Поэтому:

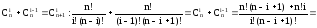
(приводим к общему знаменателю)

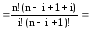
(выносим n! за скобку в знаменателе)

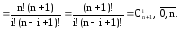
Из этого соотношения и вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов.

Докажем соотношение 1)

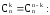
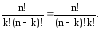
Это может использоваться при вычислениях, например, вместо можно вычислить.

Докажем соотношение 2)

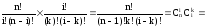
14. Бином Ньютона

Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний с повторениями

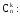
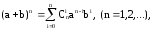
где а, b – действительные или комплексные числа.

Например:

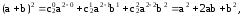
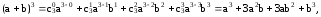
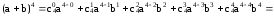
Коэффициенты называются биномиальными.

Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает:

1) базис индукции – доказательство того, что формула верна для конкретного n, например, для n=1. В нашем случае мы убедились, что формула верна для n=2,3,4. Убедимся, что она верна и для n=1.

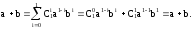
2) индукционный шаг. Предполагая, что формула верна для некоторого n, убеждаются, что тогда она верна и для n+1.

3) при истинности шагов 1 и 2 заключают, что формула верна для любого n.

Приступим к индукционному шагу.

Возьмем выражение 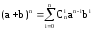и получим из него выражение для n+1. Очевидно, что это можно сделать путем умножения на a+b:

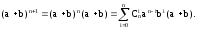
Преобразуем полученное выражение:

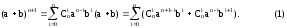
Для выполнения индукционного шага необходимо показать, что это выражение равно выражению:

.

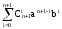Рассмотрим подвыражение выражения (1):и заменимi на i-1.

Получим 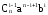, т.е. одинаковые коэффициенты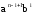перед выражениями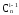,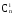для числа сочетаний в первом и втором подвыражении выражения (1).Это позволит вынести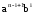за скобку. Но тогда в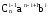не учтенn-й член подвыражения 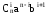(суммирование идет доn): 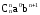тогда, учитывая его, получаем:

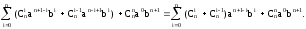
Нетрудно видеть, что 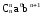можно заменить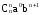на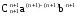, кроме того, мы уже доказали, что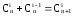, поэтому: 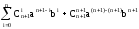, что, очевидно, равно выражению:

.

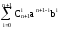По индукции получаем, что формула бинома Ньютона верна для любого n.

С использованием бинома Ньютона докажем следствие №1 о количестве подмножеств множества из n элементов:

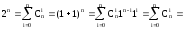
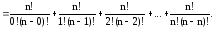
Рассмотрим следствие №2: .

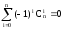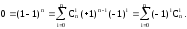
На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала:

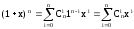. Здесь 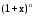– функция, производящая биномиальные коэффициенты.

При n=1 получаем 1+x, т.е. 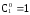(коэффициент перед 1),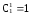(коэффициент передx).

При n=2 получаем (1+x)²=1+2x+x², т.е. 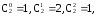и т.д.