Формулы для определения линейных потерь напора при ламинарном движении жидкости

h_л=64/Re *L/d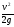. (7.11)

Формула 7.11 применяется для определения потерь напора при ламинарном движении жидкоcти в трубах круглого сечения. Обозначив 64/Re через  получим формулу Дарси-Вейсбаха

h_л=*L/d*.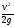

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:

Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r₀, где r₀ - радиус трубы).

12. Местные и гидравлические сопротивления

Сопротивления, возникающие при движении жидкости, называются гидравлическими сопротивлениями. На их преодоление тратится некоторая часть удельной энергии движущейся жидкости, которую называют потерей удельной энергии, или потерей напора. В уравнении Бернулли для потока реальной жидкости потери обозначаются – h_w.

Все гидравлические сопротивления разделяются на два вида: сопротивления по длине потока (h_л) или линейные, и местные сопротивления (h_м).

Гидравлические линейные сопротивления обусловливаются действием сил трения. В чистом виде эти потери возникают в прямых трубах постоянного сечения, т.е. при равномерном движении, и возрастают пропорционально длине трубы. Этот вид трения имеет место не только в шероховатых, но и в гладких трубах.

Местные гидравлические сопротивления обусловливаются местными препятствиями потоку жидкости – в виде изгиба трубы, внезапного сужения или расширения русла, при обтекании клапанов, решеток, диафрагм, кранов, которые деформируют обтекающий их поток. При протекании жидкости через местные сопротивления ее скорость изменяется, и обычно возникают вихри, т.е. движение неравномерное.

13. Истечение жидкости через отверстия и насадки. Коэффициенты истечения: сжатия, скорости и расхода.

Истечение жидкости из отверстия – одна из основных задач гидравлики. Задача об истечении сводится к определению скорости истечения и расхода вытекающей жидкости. действительная скорость истечения:

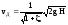, (3.48)

где  – коэффициент местного сопротивления при истечении жидкости через отверстие.

Отношение действительной скорости истечения к теоретической называется коэффициентом скорости .

коэффициент сжатия , который является отношением площади сжатого сечения струи f_СЖ к площади сечения отверстия f.

, (3.49)

где =  =Q_Д /Q_T – коэффициент расхода; показывает насколько действительный расход при истечении жидкости из отверстия уменьшается по сравнению с теоретическим в идеальном случае.

14. Гидравлический расчет трубопроводов. Потребный напор. Сопротивление трубопровода. Характеристика трубопровода.

При гидравлических расчетах трубопроводов в зависимости от их длины и гидравлических условий различают: а) короткие трубопроводы – они имеют сравнительно небольшую длину, а местные потери напора в них достаточно существенны (не менее 5…10 % от потерь напора по длине); б) длинные трубопроводы – имеют значительную протяженность, в них потери напора по длине являются основными, а местными потерями напора пренебрегают. В зависимости от геометрической конфигурации и способов гидравлического расчета различают простые и сложные трубопроводы. Простым называют трубопровод, состоящий из одной линии труб, не имеющий боковых ответвлений, т.е. трубопровод с одинаковым расходом на всем пути движения жидкости от места забора А до пункта потребления В. Сложным называют трубопровод, состоящий из основной магистрали и ряда отходящих от нее ответвлений. Основные виды сложных трубопроводов: а) параллельные (кольцевые); б) разветвленные (тупиковые).

Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Н_потр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Н_расп.

H_потр = H_ст + KQ^m

где K - величина, называемая сопротивлением трубопровода; Q - расход жидкости; m - показатель степени, который имеет разные значения в зависимости от режима течения.