10. Типовая структура и блок-схема эвм.
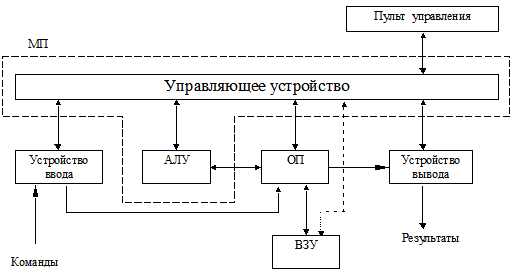
Структура типовой ЭВМ
АЛУ - предназначено для выполнения арифметических и логических преобразований над данными определенной длины.
Память - предназначена для хранения информации (данных и программ). Часто состоит из оперативной памяти и внешнего запоминающего устройства.
Как правило, данные, к которым может обращаться АЛУ находятся в ОП
ВЗУ - используется для долговременного хранения данных
Управляющее устройство - автоматически без участия человека управляет вычислительным процессом, посылая сигналы всем устройствам для реализации определенных действий. УУ в своей работе руководствуется программой. Программа состоит из команд, каждая из которых, определяет какое либо действие и операнд. Программа в свою очередь основывается на алгоритме решения поставленной задачи. Такой способ управления процессом решения задачи называется принципом программного управления. Как правило, программы хранятся также в ОП наравне с данными. Чаще всего это происходит через устройство ввода информации (клавиатура, диск). Команды выполняются в порядке следования в программе кроме команд перехода.
Устройства вывода служат для выдачи информации, результатов (например, на дисплей, принтер).
Пульт управления используется оператором для контроля хода выполнения программ и возможно для его прерывания (в ПЭВМ - отсутствует).
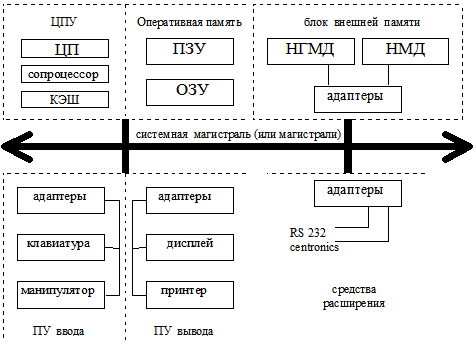
Блок схема типовой ЭВМ
11. Основы построения эвм. Элементы алгебры логики, зависимость числа выходов от числа входов.
Основные принципы построения ЭВМ были сформулированы американским учёным Джоном фон Нейманом в 40-х годах 20 века:
1. Любую ЭВМ образуют три основные компоненты: процессор, память и устройства ввода-вывода (УВВ).
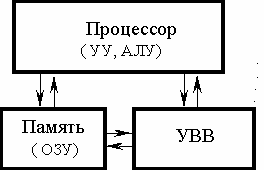
2. Информация, с которой работает ЭВМ делится на два типа:
набор команд по обработке (программы);
данные подлежащие обработке.
3. И команды, и данные вводятся в память (ОЗУ) – принцип хранимой программы.
4. Руководит обработкой процессор, устройство управления (УУ) которого выбирает команды из ОЗУ и организует их выполнение, а арифметико-логическое устройство (АЛУ) проводит арифметические и логические операции над данными.
5. С процессором и ОЗУ связаны устройства ввода-вывода (УВВ).
Архитектура современных персональных компьютеров основана на магистрально-модульном принципе. Информационная связь между устройствами компьютера осуществляется через системную шину (другое название - системная магистраль).
Схема устройства компьютера, построенного по магистральному принципу
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывания
строятся над множеством{B,
,
,
,
0, 1}, где B — непустое множество, над
элементами которого определены
триоперации:
отрицание (унарная
операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а логический ноль 0 и логическая единица 1 — константы.
12. Таблица истинности для функций двух аргументов.
|
x1=x |
1 |
1 |
0 |
0 |
|
|
|
x0=y |
1 |
0 |
1 |
0 |
Обозначение |
Название |
|
0 |
0 |
0 |
0 |
0 |
F2,0 = 0 |
тождественный ноль, детектор 0 |
|
1 |
0 |
0 |
0 |
1 |
F2,1 = x ↓ y = x NOR y = NOR(x,y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x,y) |
стрелка Пи́рса, НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, детектор 1 |
|
2 |
0 |
0 |
1 |
0 |
F2,2 = x ← y = x < y = x LT y = LT(x,y) |
инверсия обратной импликации, меньше, детектор 2 |
|
3 |
0 |
0 |
1 |
1 |
F2,3 = x = x' = ¬x = NOT1(x,y) = НЕ1(x,y) |
отрицание (негация, инверсия) первого операнда |
|
4 |
0 |
1 |
0 |
0 |
F2,4 = x → y = x > y = x GT y = GT(x,y) |
инверсия прямой импликации, больше, детектор 4 |
|
5 |
0 |
1 |
0 |
1 |
F2,5 = y = y' = ¬y = NOT2(x,y) = НЕ2(x,y) |
отрицание (негация, инверсия) второго операнда |
|
6 |
0 |
1 |
1 |
0 |
F2,6 = x ⊕ y = x XOR y = XOR(x,y) = x >< y = x <> y = x NE y = NE(x,y) |
сложение по модулю 2, исключающее «или», сумма Жегалкина[5], не равно |
|
7 |
0 |
1 |
1 |
1 |
F2,7 = x | y = x NAND y = NAND(x,y) = x НЕ-И y = НЕ-И(x,y) |
штрих Ше́ффера, НЕ-И, 2И-НЕ, антиконъюнкция |
|
8 |
1 |
0 |
0 |
0 |
F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x,y) = x И y = И(x,y) = min(x,y) |
конъюнкция, 2И, минимум, детектор 8 |
|
9 |
1 |
0 |
0 |
1 |
F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x,y) |
эквивалентность, равенство |
|
10 |
1 |
0 |
1 |
0 |
F2,10 = YES2(x,y) = ДА2(x,y) = y |
второй операнд |
|
11 |
1 |
0 |
1 |
1 |
F2,11 = x → y = x ⊃ y = x ≤ y = x LE y = LE(x,y) |
прямая (материальная) импликация (от первого аргумента ко второму), меньше или равно |
|
12 |
1 |
1 |
0 |
0 |
F2,12 = YES1(x,y) = ДА1(x,y) = x |
первый операнд |
|
13 |
1 |
1 |
0 |
1 |
F2,13 = x ← y = x ⊂ y = x ≥ y = x GE y = GE(x,y) |
обратная импликация (от второго аргумента к первому), больше или равно |
|
14 |
1 |
1 |
1 |
0 |
F2,14 = x ∨ y = x + y = x OR y = OR(x,y) = x ИЛИ y = ИЛИ(x,y) = max(x,y) |
дизъюнкция, 2ИЛИ, максимум |
|
15 |
1 |
1 |
1 |
1 |
F2,15 = 1 |
тождественная единица, тавтология |