Указания к решению задач

При решении задач, в которых заданы поршни или системы поршней, необходимо использовать уравнения равновесия, отражающие равенство нулю алгебраической суммы всех сил, действующих на поршень (систему поршней) в направлении выбранных осей координат:

. (2.11)

При решении задач, в которых по условию задачи имеется плоская стенка, установленная с возможностью вращения относительно некоторой оси, необходимо использовать уравнение равновесия, отражающее равенство нулю алгебраической суммы всех моментов сил, действующих на стенку относительно оси

. (2.12)

Каждый из моментов сил определяется как произведение силына ее плечо. Плечо силы- это кратчайшее расстояние от центра вращения до направления действия силы.

Пример 5

Рисунок 2.2 – К примеру 5

Резервуар (рис. 2.2) выполнен из двух полых цилиндров: верхнего диаметром d₁= 1 м и нижнего диаметром d₂ = 3 м, высотой H₂ = 3м и наполнен водой. Глубина наполнения резервуара Н₁ = 4,5 м. Собственный вес резервуара G = 10кН. Определить силу избыточного давления воды на дно резервуара и силу, действующую на опоры.

Решение

Определяем величину избыточного давления на днище резервуара:

1000· 9,81 · 4,5 = 44145 Па.

Определяем силу избыточного давления на днище:

Сила давления жидкости на днище резервуара является внутренней силой, и она не передается на опоры, на которых установлен резервуар. Опоры воспринимают вес резервуара и воды.

Находим вес воды:

Вычисляем величину реакции опор:

которая оказалась на 30% меньше силы избыточного гидростатического давления на днище .

Пример 6

точка С – центр тяжести (масс) щита; точка Д – центр давления силы Ризб Рисунок 2.3 – К примеру 6

Определить величину и точку приложения силы давления на прямоугольный щит шириной b = 2 м, наклоненный к горизонту под углом α = 60º (рис. 2.3). Глубина наполнения резервуара водой равна Н = 4 м.

Решение

Находим величину площади смоченной поверхности:

Определяем глубину погружения центра тяжести прямоугольного щита:

Сила избыточного гидростатического давления по формуле (2.1) при числовых значениях – 1000 кг/м³; – 9,81 м/с²; – 2 м иS – 9,24 м² равна:

Высота щита l (рис. 2.3):

Координата центра давления, т.е. точка приложения силы Р_изб на щит прямоугольной формы, полученная из решения формулы (2.3), равна:

(2.13)

Пример 7

Рисунок 2.4 – К примеру 7

Определить величину и точку приложения силы избыточного гидростатического давления жидкости на вертикальный прямоугольный щит (рис. 2.4) шириной b = 2 м, если глубина жидкости перед щитом Н = 3 м. Жидкость – вода.

Решение

При решении задачи применим формулы (2.1) и (2.2), принимая во внимание, что при угле наклона щита к горизонту α = 90º (вертикальный щит): sin α = sin 90º = 1.

Имеем величину силы избыточного гидростатического давления

Точка приложения данной силы расположена на вертикальной оси симметрии щита на глубине погружения

Пример 8

В боковой вертикальной стенке резервуара (рис. 2.5) имеется отверстие, перекрываемое плоским прямоугольным щитком с размерами а = 0,5 м и b = 2 м. Уровень воды в резервуаре Н = 3 м. Определить величину и точку приложения силы избыточного гидростатического давления, действующего на щиток.

Решение

Силу избыточного гидростатического давления на щит находим по формуле (2.1):

где – глубина погружения центра масс, равная:

– площадь прямоугольного щитка:

– плотность воды,

.

Н – глубина наполнения резервуара; а – высота щитка; b – ширина щитка;

глубина погружения центра масс щитка; – сила избыточного

гидростатического давления на щиток; – глубина погружения центра давления

Рисунок 2.5– К примеру 8

Глубину погружения центра давления находим по формуле (2.5)

где

- центральный момент инерции щитка;

Пример 9

Рисунок 2.6 – Схема щита, перекрывающего канал

Прямоугольный щит, перекрывающий канал шириной b = 5 м, закреплен шарнирно в точке О (рис. 2.6).

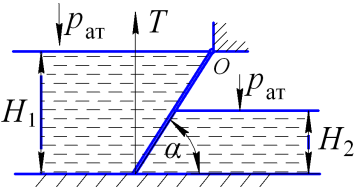
Определить усилие Т, необходимое для подъема щита, если угол его наклона к горизонту α = 60º. Глубина воды слева от щита Н₁ = 4 м, а справа от щита равна Н₂ = 2 м. Весом щита пренебречь.

Решение

Схему сил, действующих на щит, выполним на отдельном рисунке (рис. 2.7).

д1, д2 – центры давлений сил соответственно слева и справа; Ризб.1, Ризб.2 – силы избыточного давления на щит соответственно слева и справа Рисунок 2.7 – Схема сил, действующих на щит

Алгебраическая сумма моментов всех сил относительно точки О равна нулю (условие равновесия щита):

, (2.14)

где – сила избыточного гидростатического давления, действующего слева от щита;

–сила избыточного гидростатического давления, действующего справа от щита;

Т – потребное усилие, прикладываемое к щиту;

, и AB – плечи соответствующих сил.

Согласно равенства (2.14) искомое усилие можно определить по формуле:

(2.15)

Найдем входящие в данное соотношение параметры.

Находим высоту щита:

Площади смоченной поверхности щита:

- слева

- справа

Силы избыточного давления на щит:

- слева

- справа

Поскольку центры давления смоченных поверхностей для прямоугольных стенок погружены на глубину 2/3 их высоты, то плечи соответствующих сил равны:

С учетом результатов предыдущих вычислений

= 3,85 м ; = 3,08 м;АВ = 2,31 м

по формуле (2.15) находим величину усилия Т, необходимого для подъема щита: