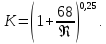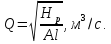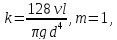- •Содержание
- •Методические рекомендации к решению задач расчетно-графической работы
- •Правила оформления ргр
- •Принятые обозначения
- •Тема 1. Гидростатическое давление и его измерение
- •Указания к решению задач
- •Рисунки 1.7…1.28 к задачам темы 1
- •Тема 2. Силы гидростатического давления на плоские и криволинейные поверхности
- •2.1. Сила давления жидкости на плоские поверхности
- •Указания к решению задач
- •2.2.Cила давления жидкости на криволинейные поверхности
- •Рисунки 2.13…2.37 к задачам темы 2
- •Тема 3. Уравнение бернулли. Гидравлические сопротивления
- •Указания к решению задач
- •Рисунки 3.7…3.18 к задачам темы 3
- •Тема 4. Гидравлический расчет напорных трубопроводов
- •4.1. Расчет простого трубопровода
- •4.2. Расчет сложных трубопроводов
- •4.3. Трубопровод с непрерывной раздачей жидкости по пути
- •Указания к решению задач
- •Рисунки 4.8…4.22 к задачам темы 4
- •Тема 5. Гидравлический удар в трубопроводах
- •Тема 6. Насосная установка и ее характеристика. Работа насоса на сеть
- •Указания к решению задач
- •Рисунки 6.5…6.13 к задачам темы 6
- •Тема 7. Расчет объемного гидропривода
- •Указания к решению задач
- •Рисунки 7.7….7.16 к задачам темы 7
- •Тема 8. Основы сельскохозяйственного водоснабжения
- •Источники водоснабжения
- •Водоприемные сооружения
- •Водонапорное оборудование
- •Напорно-регулирующие сооружения
- •Основные методы и технологические процессы обработки воды
- •Системы подачи и распределения воды
- •Классификация систем водоснабжения
- •Указания к решению задач
- •Приложения
- •Литература
Рисунки 3.7…3.18 к задачам темы 3
|
| |
|
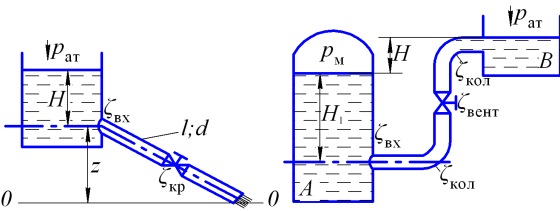
Рисунок 3.7 |
Рисунок 3.8 |
|
| |
|
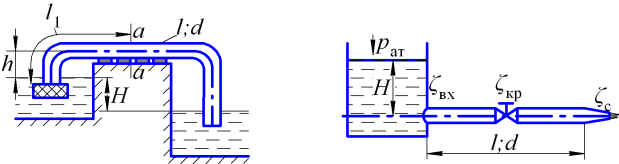
Рисунок 3.9 |
Рисунок 3.10 |
|
| |
|
Рисунок 3.11 |
Рисунок 3.12 |
|
| |
|
| |
|
Рисунок 3.13 |
Рисунок 3.14
|
|
| |
|
Рисунок 3.15 |
Рисунок 3.16 |
|
| |
|
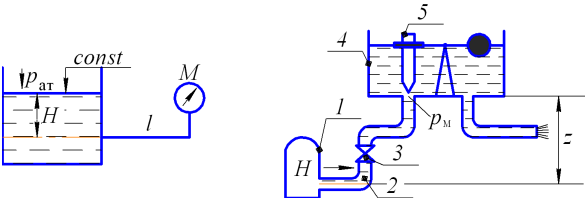
Рисунок 3.17 |
1 – насос; 2 – нагнетательная линия; 3 – кран; 4 – поплавковая камера; 5 – игла
Рисунок 3.18 |
Тема 4. Гидравлический расчет напорных трубопроводов
Трубопроводом называют конструктивную единицу, предназначенную для транспортирования капельных или газообразных жидкостей.
Все многообразие трубопроводов, используемых в современной технике и инженерных коммуникациях, классифицируют по следующим признакам:
в зависимости от отсутствия и наличия свободной поверхности: напорные и безнапорные. В напорных трубопроводах свободная поверхность отсутствует и трубопроводы работают полными сечениями;
в общем случае: простые и сложные. Простой трубопровод – это напорный трубопровод постоянного внутреннего диаметра, выполненный из одного и того же материала без ответвлений.
Все остальные трубопроводы являются сложными.
в зависимости от соотношения потерь напора
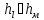 (4.1)
(4.1)
различают гидравлически длинные и гидравлически короткие:
- гидравлически длинными считают трубопроводы, в которых влияние местных потерь напора невелико и ими можно пренебречь или принять приближенно
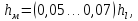 (4.2)
(4.2)
тогда
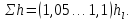 (4.3)
(4.3)
- гидравлически короткими считают трубопроводы, в которых местные потери напора соизмеримы или превышают потери напора на трение:
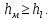 (4.4)
(4.4)
В
формулах (4.3) и (4.4) потери напора на трение
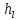 определяют
по формуле Дарси-Вейсбаха, а местные
определяют
по формуле Дарси-Вейсбаха, а местные
 ,
пользуясь формулой Вейсбаха.
,
пользуясь формулой Вейсбаха.
вида материала стенок трубопровода:
- металлические (стальные, чугунные, из алюминиевых сплавов и т.д.);
- неметаллические (асбестоцементные, полипропиленовые, стеклянные и т.д.);
вида транспортируемой жидкости: бензопроводы, топливопроводы, водопроводы, молокопроводы и т.д.
4.1. Расчет простого трубопровода
Уравнения, которыми пользуются при его расчете, следующие:
- уравнение Бернулли, являющегося уравнением баланса удельных энергий (м):
|
|
(4.5) |
где
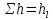 ,
поскольку местные потери напора малы
,
поскольку местные потери напора малы
 ;
;
- уравнение неразрывности, являющегося балансом расхода (м3/с):
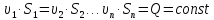 (4.6)
(4.6)
- уравнение Дарси-Вейсбаха для определения потерь напора на трения (м):
|
|
(4.7) |
После введения следующих обозначений в уравнение Бернулли :
|
- потребный напор |
|
(4.8) |
|
- статический напор |
|
(4.9) |
а
также выразив скоростную высоту в
уравнении Дарси-Вейсбаха через расход
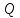 с последующей подстановкой в уравнение
(4.6) получим окончательное решение
уравнения Бернулли:
с последующей подстановкой в уравнение
(4.6) получим окончательное решение
уравнения Бернулли:
 (4.10)
(4.10)
|
где |
|
– удельное сопротивление трубопровода (с2/м6), (4.11) справочная величина, см. Приложения 8;9,10; |
|
|
l |
– длина трубопровода, м; |
|
|
|
– расход жидкости, м3/с; |
|
|
m |
– показатель степени, зависящий от режима течения жидкости:
|
Формула
(4.11), как и значение А
в ней справедливы для турбулентного
режима в области квадратичного
сопротивления, то есть при условии
выполнения неравенства:  (4.12)
(4.12)
Значения предельных скоростей υкв в зависимости от величины расхода и материала труб приведены в табл. 4.1
Таблица 4.1
Значения предельных скоростей в зависимости от материала труб
|
Трубы |
Предельные скорости υкв
, м/с при
|
|
Стальные Чугунные Асбестоцементные Полиэтиленовые |
1…1,3 1,1…1,5 1,1…1,7 1…2 |
При условии невыполнения неравенства (4.12) в формулу (4.10) при турбулентном режиме вводят поправку:
 (4.13)
(4.13)
где К – поправочный коэффициент на неквадратичность сопротивления, равный:
|
|
(4.14) |
При
расчете простых трубопроводов в области
квадратичного сопротивления и
 =0
возможны три основные задачи:
=0
возможны три основные задачи:
Задача
1.
Исходные данные: расход
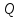 ,
длинаl
и диаметр трубы d,
а также материал трубы. Найти потребный
напор
,
длинаl
и диаметр трубы d,
а также материал трубы. Найти потребный
напор
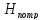 .
.
Решение. По заданному d и материалу трубы по таблицам Приложений 8, 9, 10 определяют величину удельного сопротивления А, с2/м6.
Для
горизонтального трубопровода
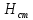 =
0,
значит
=
0,
значит
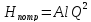 ,
м (4.15)
,
м (4.15)
Для
негоризонтальных трубопроводов, то
есть
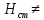 0
0
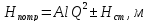 (4.16)
(4.16)
Задача
2.
Исходные данные: располагаемый напор
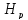 ,
длинаl,
диаметр трубы d
и материал трубы. Найти расход
,
длинаl,
диаметр трубы d
и материал трубы. Найти расход
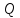 .
.
Решение. По заданному d и материалу трубы по таблицам Приложений 8, 9, 10 определяют величину удельного сопротивления А, с2/м6.
Тогда при квадратичном режиме сопротивления:
|
|
(4.17) |
Задача
3.
Исходные данные: расход
 ,
располагаемый напор
,
располагаемый напор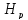 ,
длинаl
и материал трубы; Нст
= 0. Найти диаметр трубы d.
,
длинаl
и материал трубы; Нст
= 0. Найти диаметр трубы d.
|
|
|
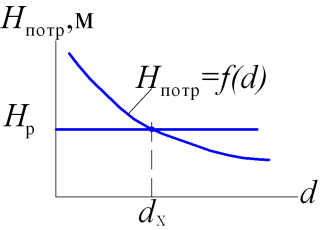
Рисунок 4.1 – Графическое определение диаметра трубы
|
Задают
произвольно несколько (3…5) значений
d,
для которых по таблицам Приложений 8,
9, 10 определяют величины соответствующих
значений А.
Затем вычисляют ряд значений потребного
напора и строят график зависимости
Нпотр
= f
(d).
Графически при заданном значении
располагаемого напора Нр
по кривой определяют dx
(рис. 4.1). В соответствии с ГОСТ выбирают
ближайший стандартный диаметр d
большего расчетного значения и уточняют
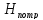 на выполнение неравенства:
на выполнение неравенства:
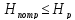 .
.
При расчете простого гидравлически короткого трубопровода суммарные потери напора складываются из потерь напора на трение по длине и местных потерь:
 . (4.18)
. (4.18)
Для принятых ранее обозначений (4.9) и (4.10) уравнение Бернулли в общем случае примет вид:
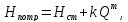 (4.19)
(4.19)
где для турбулентного течения:
|
|
(4.20) |
для ламинарного течения:
|
|
(4.21) |
где v – кинематический коэффициент вязкости транспортируемой
жидкости, м2/с;
l – длина трубопровода, м;
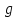 –ускорение
свободного падения, м/с2.
–ускорение
свободного падения, м/с2.
В принятой практике расчета гидравлически коротких трубопроводов местные потери принято заменять эквивалентной длиной lэ, равной:
|
|
(4.22) |
где
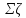 – сумма коэффициентов местных
сопротивлений, значения которых
определяют по данным Приложения 6;
– сумма коэффициентов местных
сопротивлений, значения которых
определяют по данным Приложения 6;
А – удельное сопротивление трубы, которое при квадратичном законе
сопротивления А = Акв. (4.23)
При неквадратичном законе сопротивления:
А = К ·Акв., (4.23)
где К определяют по формуле (4.14).
С учетом эквивалентной длины потребный напор в неквадратичной области сопротивления для гидравлически коротких трубопроводов равен:
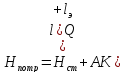 . (4.25)
. (4.25)
|
|
|
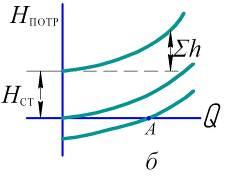
Рисунок 4.2 – Кривые потребного напора |
Расчет простых гидравлически коротких трубопроводов аналогичен расчету гидравлически длинных трубопроводов и в основном сводится к решению тех же трех задач.
Согласно
формул (4.17)…(4.19) зависимость Нпотр
= f(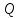 ),
называемаякривой
потребного напора,
приведена
на рисунке 4.2.
),
называемаякривой
потребного напора,
приведена
на рисунке 4.2.

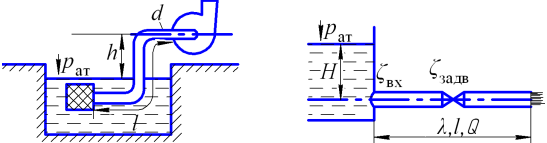
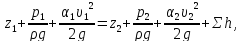
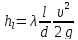
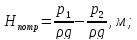
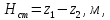
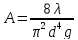
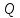
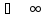 , m
= 2.
, m
= 2. = 2…100 дм3/с
= 2…100 дм3/с