- •Курсовая работа
- •6 Вариант
- •Содержание
- •Введение
- •1 Стоимость денег во времени, функции сложного процента
- •1.2 Текущая стоимость единицы
- •1.3 Накопление денежной единицы за период
- •Задача № 3
- •1.4 Формирование фонда возмещения
- •1.5 Взнос на амортизацию единицы
- •1.6 Текущая стоимость аннуитета
- •2 Анализ рынка недвижимости
- •3 Применение методических подходов к оценке стоимости недвижимости
- •3.1.2 Дисконтирование будущих потоков
- •3.2 Рыночный подход оценки недвижимости
- •3.2.1 Метод сравнения продаж
- •3.2.2. Валовой рентный мультипликатор
- •3.3 Затратный метод
- •4 Определение наилучшего и наиболее эффективного варианта использования недвижимости
- •4.1 Анализ наилучшего и наиболее эффективного использования свободного земельного участка
- •Задача № 16
- •4.2 Анализ наилучшего и наиболее эффективного использования застроенного земельного участка
- •5 Ипотечно-инвестиционный анализ
- •5.1 Оценка эффективности привлечения заемных средств
- •5.2 Оценка кредитуемой недвижимости
- •5.3 Расчет стоимости кредита
- •5.3.1 Расчет постоянного ипотечного кредита
- •5.3.2 Расчет ипотечного кредита с фиксированным платежом основной суммы долга
- •6 Оценка стоимости инвестиций в недвижимость
- •Заключение
- •Список источников:
1 Стоимость денег во времени, функции сложного процента
Стоимость недвижимости, как и стоимость денег, меняется во времени. Известно, что одна и та же сумма денег, полученная в разные моменты времени, обладает разной стоимостью. Стоимость недвижимости определяется текущей стоимостью доходов, ожидаемых от нее в будущем. Теория стоимости денег во времени позволяет рассчитать и уравнять денежные потоки, приходящиеся на разные моменты времени.
Денежные потоки – суммы денег, относящиеся к определенным моментам времени. Основными операциями, позволяющими сопоставить разновременные деньги, являются операции накопления и дисконтирования.
Накопленная сумма денежной единицы
Накопленная сумма единицы - первая функция денег. Данная функция показывает, какая сумма будет накоплена на счете к концу определенного периода при заданной ставке дохода, если сегодня положить 1 платеж. Функция связана с понятиями "простой" и "сложный" процент.
Простой процент - приращение дохода на вложенную сумму денег по единой процентной ставке в течение всего срока.
Сложный процент - приращение дохода на вложенную сумму денег по сумме остатка предыдущего периода времени в течение срока инвестиций или кредита.
Расчет простого процента:
![]()
Расчет сложного процента:
![]()
PV- настоящий вклад, руб (у.е.);
i - ставка процента (далее - i; в долях 5%=0,05), %;
n - период (срок) вклада, лет (мес.).
При ежеквартальном начислении (k=4):
![]()
Задача № 1
Условие: Определить какая сумма будет накоплена на счете к концу 8,5 года, если сегодня положить на счет, приносящий 13 % годовых, 2300 руб. Начисление осуществляется в конце каждого квартала.
Решение:
![]()
График:
1.2 Текущая стоимость единицы
Текущая стоимость единицы - вторая функция денег. Смысл заключается в том, чтобы при заданной ставке дисконта дать оценку текущей стоимости тех денег, которые могут быть получены в конце определенного периода.
Определяется по формулам:
![]()
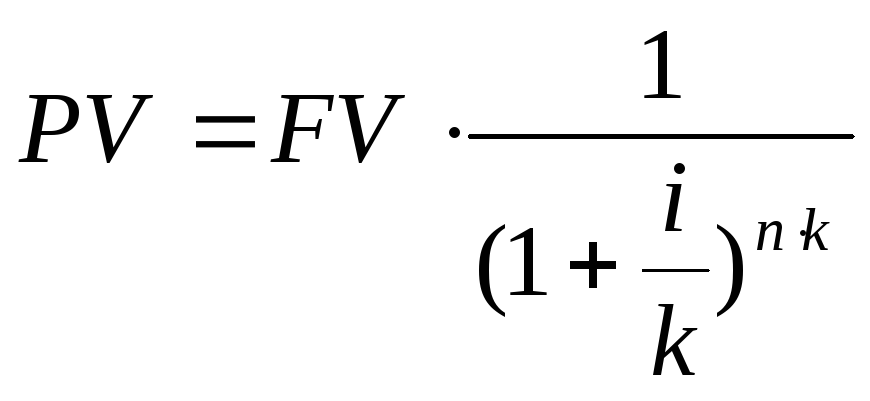
PV - настоящий платеж, руб;
FV - будущий платеж (Кn), руб;
1/(1+i)n - фактор текущей стоимости единицы;
k - количество начислений в год (период).
Задача № 2
Условие: Определить текущую стоимость 5250 руб., которые будут получены в конце 6-го года при 12 % ставке дисконта. Начисление процентов осуществляется в конце каждого полугодия.
Решение:
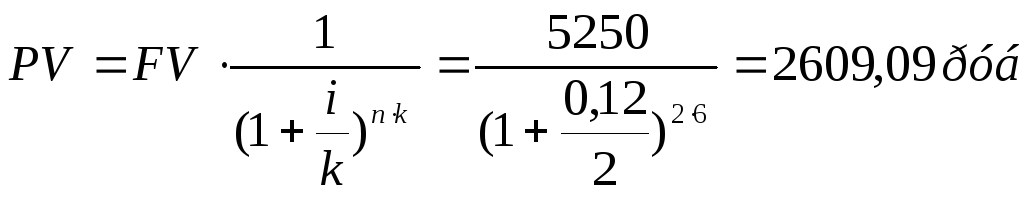
1.3 Накопление денежной единицы за период
Накоплением денежной единицы за период или текущей стоимостью единицы реверсии - третья функция денег. На основе использования данной функции определяется будущая стоимость серии равновеликих периодических платежей. Экономический смысл – показывает, какая сумма будет накоплена на счете при заданной ставке, если регулярно в течении определенного срока откладывать на счет одну денежную единицу.
Определяется по формулам:
Обычный аннуитет:
![]()
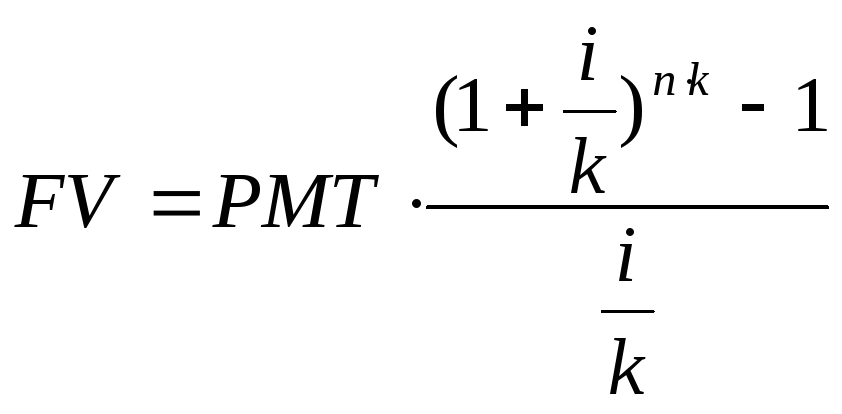
Авансовые платежи:
![]()
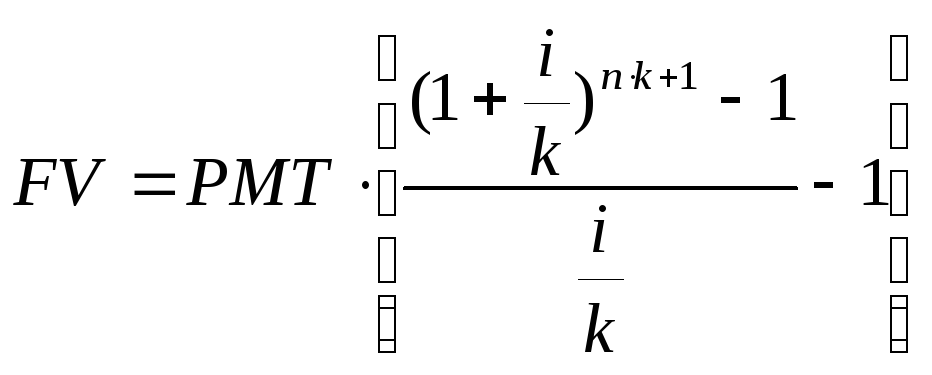
k - количество начислений в год (период);
PMT - регулярный периодический платеж.
Задача № 3
Условие: Определить сумму которая будет накоплена на счете, приносящем 12% годовых к концу 16 мес., если ежемесячно откладывать на счет 2000 рублей. При условии:
а) Платежи поступают в конце каждого месяца;б) Платежи поступают в начале каждого периода;
Решение:
а)
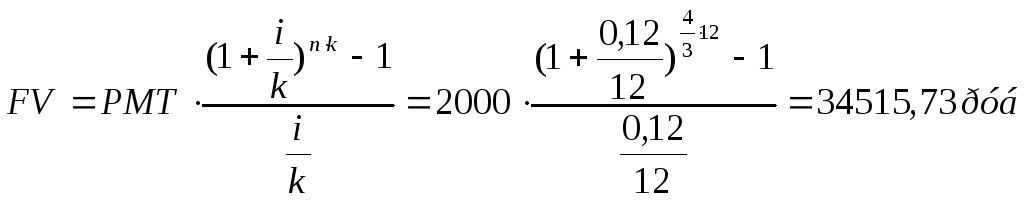
б)