Блок питания

БЛОК СЧЕТА

1.2 Синтез счетчиков

Синтез счетчика сводится к определению оптимальной структуры и построению его принципиальной схемы. Под оптимальной понимается структура счетчика, содержащая минимальное количество триггеров и связей между ними, при которой обеспечивается выполнение счетчиком требуемых функций с заданными значениями параметров.

Основными исходными данными для синтеза счетчика являются:

1. модуль счета (емкость счетчика) Кс ;

2. порядок изменения состояний счетчика;

3. режим счета (суммирующий, вычитающий или реверсивный);

4. требуемая разрешающая способность счетчика

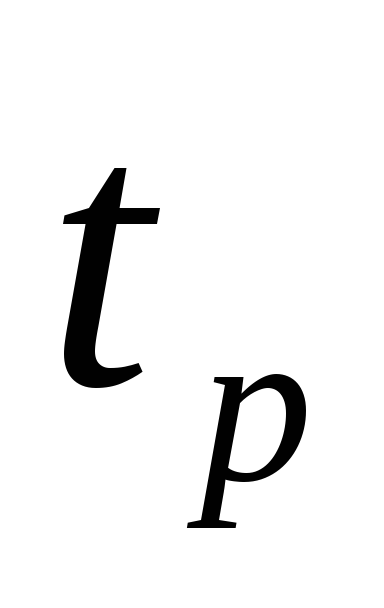
5. необходимое время установки кода счетчика

Исходя из заданной емкости и модуля счета Кс, определяют необходимое количество m триггеров в счетчике. Для двоичных счетчиков , недвоичных -, где- двоичный логарифм числа Кс, округленный до большего ближайшего целого числа. Разрешающую способность и время установки кода счетчика учитывают при выборе серии интегральных микросхем и типа триггера, а также при выборе способа переключения триггеров (последовательного или параллельного). При выборе серии триггера необходимо учитывать условие

где - максимально допустимая для данного триггера частота следования входных сигналов. Время установки кода является основным фактором, определяющим выбор способа переключения триггеров. При последовательном способе запуска триггеров растет вm раз с увеличением числа m триггеров в счетчике, а при параллельном - не зависит от величины m. Поэтому более предпочтительным, как правило, является параллельный способ запуска триггеров. Последовательный способ целесообразно применять в счетчиках, используемых в качестве делителе частоты. Определив количество разрядов (триггеров) счетчика m, выбрав серию интегральных микросхем и способ переключения триггеров, приступают к разработке структурной схемы счетчика. Основной задачей синтеза счетчика является определение оптимальных логических функций , связывающих между собой входы и выходы всех триггеров.

2. Разработка функциональной схемы.

2.1 Составление таблицы функционирования счет­чика .

В суммирующем счетчике номер последующего состояния на единицу больше номера предыдущего состояния. Поэтому для суммирующего счетчика с Kc = 10 работающев в коде 4-2-2-1 таблица функционирования счетчика будет иметь вид представленный в таблице.

№	Q3n	Q2n	Q1n	Q0n		Q3n+1	Q2n+1	Q1n+1	Q0n+1		F3	F2	F1	F0
0	0	0	0	0		0	0	0	1		0	0	0	
1	0	0	0	1		0	0	1	0		0	0		
2	0	0	1	0		0	0	1	1		0	0	1	
3	0	0	1	1		0	1	1	0		0		1	
4	0	1	1	0		0	1	1	1		0	1	1	
5	0	1	1	1		1	0	1	0				1	
6	1	0	1	0		1	0	1	1		1	0	1	
7	1	0	1	1		1	1	1	0		1		1	
8	1	1	1	0		1	1	1	1		1	1	1	
9	1	1	1	1		0	0	0	0					

Таблица функционирования счетчика работающего в коде 4-2-2-1.

2.2 Составление карт Карно функций управле­ния входов J и K для каждого триггера.

Исходя из значений функций переходов, строим карты функций переходов F₃, F₂, F₁, F₀соответственно для триггеров Т3,Т2,Т1,Т0.

F3	00	01	11	10
00	0	0	0	0
01	-	-		0
11	-	-		1
10	-	-	1	1

F2	00	01	11	10
00	0	0		0
01	-	-		1
11	-	-		1
10	-	-		0

F1	00	01	11	10
00	0		1	1
01	-	-	1	1
11	-	-		1
10	-	-	1	1

F0	00	01	11	10
00				
01	-	-		
11	-	-		
10	-	-		

Исходя из значений функций переходов строим карты Карно. Выбираем триггер JK, т. к счетчики на RS-триггерах имеют большее количество связей между входами и выходами разрядов, а при использовании D-триггеров в разрядах счетчика возникает необходимость в применении дополнительных логических элементов, вследствие чего возрастает потребляемая мощность и уменьшается максимальная рабочая частота.

В результате получается набор карт, отражающих значения логических функций на всех входах каждого триггера в зависимости от состояния счетчика.

J3	00	01	11	10
00	0	0	0	0
01	-	-	1	0
11	-	-	X	X
10	-	-	X	X

J2	00	01	11	10
00	0	0	1	0
01	-	-	X	X
11	-	-	X	X
10	-	-	1	0

J1	00	01	11	10
00	0	1	X	X
01	-	-	X	X
11	-	-	X	X
10	-	-	X	X

J0	00	01	11	10
00	1	X	X	1
01	-	-	X	1
11	-	-	X	1
10	-	-	X	1

K3	00	01	11	10
00	X	X	X	X
01	-	-	X	X
11	-	-	1	0
10	-	-	0	0

K2	00	01	11	10
00	X	X	X	X
01	-	-	1	0
11	-	-	1	0
10	-	-	X	X

K1	00	01	11	10
00	X	X	0	0
01	-	-	0	0
11	-	-	1	0
10	-	-	0	0

K0	00	01	11	10
00	X	1	1	X
01	-	-	1	X
11	-	-	1	X
10	-	-	1	X

2.3 Составление минимизированных логиче­ских уравнений.

С помощью карт Карно получаем минимизированные логические уравнения для каждого из входов каждого триггера.

J₃ = Q_2* Q₀ J₂ = Q_1* Q₀ J₁ = Q₀ J₀ =1

K₃ = Q_2* Q₀ K₂ = Q₀ K₁ = Q_0* Q_2* Q₃ K₀ =1

2.4 Составление функциональной схемы.

Из уравнений следует, что это значит, что на J и K входы нулевого триггера нужно подать потенциал, соответствующий логической единице, на остальные триггеры подать импульсы переноса соответствующие приведенным функциям управления.

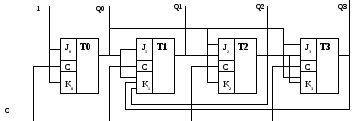
Схема счетчика, построенная на JK-триггерах и реализующая логические функции управления триггерами.

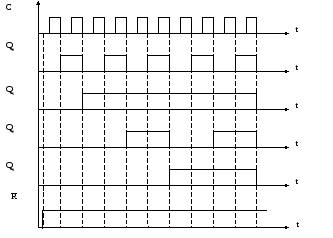
Временная диаграмма счетчика, работающего в коде 4-2-2-1.