
Лабораторки ФИЗИКА
.pdf
12. Визначте відносно теоретичну похибку розрахунку: |
|
||||||
δ = |
|
|
BT − B |
|
|
100% , |
(15.17) |
|
|
||||||
|
|
||||||
|
|
|
|
|
|||
|
|
|
BT |
|
|||
де BT - теоретичне значення газової сталої для повітря (табл. Д2). 13.Сформулюйте та запишіть висновок до роботи.
Контрольні запитання до лабораторної роботи № 15
Термодинамічні параметри, одиниці їх вимірювання. Рівняння Клапейрона-Менделєєва. Фізичний зміст універсальної газової сталої. Основне рівняння молекулярно-кінетичної теорії ідеальних газів. Класифікація похибок.
Лабораторна робота №16
ДОСЛІДЖЕННЯ КОЛИВАНЬ СИСТЕМИ ІЗ ЗОСЕРЕДЖЕНИМИ ПАРАМЕТРАМИ
Мета роботи: визначити коефіцієнт жорсткості пружини статичним та динамічним методами.
Обладнання: вимірювальна лінійка, набір тягарців різної маси, дві різні пружини, секундомір.
Опис лабораторної установки
|
3 |
2 |
4 |
|
|
|
L0 |
|
L |
|
xст |
1 |
|
|
Рис. 16.1 |
Лабораторна |
установка |
||
(рис. 16.1) |
складається |
з |
|
Π -подібного кронштейна (2), закріпленого на масивній підставці (1). На гачки (3) в перекладині кронштейна підвішують досліджувані пружини, а до пружин - тягарці з масами m. Вертикально закріплена масштабна лінійка (4) дає змогу
61
вимірювати довжину пружин у навантаженому L та ненавантаженому L0
станах і визначити величину статичного розтягу xcm . Тривалість коливань тягарців на пружинах, вимірюють секундоміром.
Короткі теоретичні відомості
Пружина з тягарцем є прикладом систем із зосередженими параметрами: вся маса системи зосереджена у центрі мас тягарця, пружні властивості – у пружині.
Коливанням називають рух або процес, що характеризується повторюваністю в часі.
Визначення коефіцієнта жорсткості статичним методом.
У положенні рівноваги, вага кульки врівноважується силою пружності: kcm xcm = mg , (16.1)
де kcm xcm - сила пружності при статичному розтягу пружини (за законом Гука); xcm = L − L0 - статичний розтяг пружини; m - маса тягарця; g - прискорення вільного падіння
З виразу (16.1) одержимо:
k = |
mg |
(16.2) |
cm xcm
Визначення коефіцієнта жорсткості динамічним методом.
Періодичними процесами називають такі зміни стану системи, при яких вона багато разів через деякі рівні проміжки часу повертається в один і той же стан.
Час, протягом якого система здійснює одне коливання, називається періодом T :
T = |
t |
, |
(16.3) |
|
|||
|
N |
|
|
де t – час протягом якого система здійснює N коливань. |
|
||
Пружинний маятник - це система, що складається з абсолютно |
|||
пружної пружини та підвішеного до неї вантажу масою |
m, який здійснює |
||
гармонічні коливання під дією сил пружності. |
|
||
62
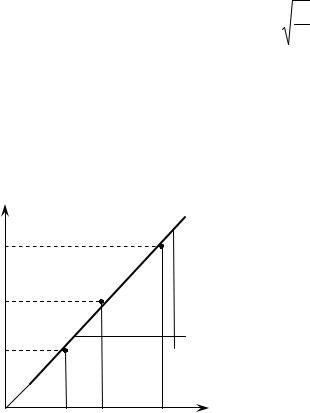
Період коливань пружинного маятника:
T = 2π m , (16.4) k
де k - коефіцієнт жорсткості пружини. З виразу (16.4):
|
|
|
T 2 = |
4π 2 |
m |
|
|
(16.5) |
|
|
|
|
k |
|
|
||||
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
Отриманий вираз (16.5) свідчить |
||||
T 2 |
|
|
про те, що квадрат періоду T 2 |
коливань |
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
(T 2 ) |
пружинного |
|
маятника є |
лінійною |
|||
2 |
|
функцією маси m тягарця (рис. 16.2), а |
|||||||
T2 |
|
|
|||||||
m |
|
|
|
|
|
4π |
2 |
|
|
|
|
|
|
|
|
|
|
||
T12 |
|
|
величина |
|
є кутовим коефіцієнтом |
||||
|
|
k |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
графіка T 2 (m) і дорівнює тангенсу кута |
||||||
m1 m2 |
m3 |
m |
нахилу графіка до вісі абсцис. |
|
|||||
|
|
|
|
||||||
Рис. 16.2 |
|
|
|
|
Виходячи з побудови (рис. 16.2) |
||||
та згідно (16.5), коефіцієнт жорстокості пружини може бути визначеним динамічним способом:
kдин = 4π |
2 |
m |
(16.6) |
|
|
(T 2 ) |
|
||
Порядок виконання роботи
Визначення коефіцієнту жорсткості пружини статичним методом.
1.Визначте за вимірювальною шкалою поділку, що відповідає положенню кінця недеформованої пружини L0 .
2.Підвісьте до пружини тягарець та визначте поділку, що відповідає положенню кінця деформованої пружини Li , та знайдіть xcm,i = Li − L0 .
3.Користуючись виразом (16.2) розрахуйте величину kcm,i .
4.Повторіть пп. 2-3 для решти тягарців.
5.Виконайте пп. 1-4 для іншої пружини.
6.Результати вимірювань та розрахунку занесіть до звітної таблиці 16.1.
63
|
|
Таблиця 16.1 |
|
|
|
№ |
mi , кг L0 , м Li , м xcm,i , м kcm,i , Н/м |
kcm , Н/м |
1
2
пружина
3
№ 1
1
2
пружина
3
№ 2
7. Розрахуйте середнє значення коефіцієнту пружності для кожної з пружин:
|
|
1 |
n |
|
|
kcm |
= |
∑kcm,i |
(16.7) |
||
|
|||||
|
|
n i=1 |
|
||
де n - кількість значень.
Визначення коефіцієнту жорсткості пружини динамічним методом.
1.Підвісьте на пружину один із тягарців, відтягніть пружину на 3-4 см
донизу, відпустіть та виміряйте секундоміром час ti , за який система здійснить N =10 коливань.
2.За формулою (16.3) розрахуйте період коливань Ti та знайдіть Ti2 .
3.Повторіть пп. 1-2 для решти тягарців.
4.Результати вимірювань та розрахунків занесіть до звітної таблиці 16.2.
|
|
|
|
|
|
|
|
Таблиця 16.2 |
|
|
|
|
|
|
|
|
|
№ |
|
mi , кг |
ti , с |
N |
Ti , с |
T 2 |
, с2 |
kдин , Н/м |
|
|
|
|
|
|
i |
|
|
1 |
пружина |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
№ 1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
пружина |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
№ 2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.Для кожної з пружин побудуйте графіки залежності T 2 (m) і за формулою (16.6) розрахуйте коефіцієнти жорсткості kдин .
6.Для кожної з пружин оцініть розбіжність отриманих результатів:
σ = 2 |
|
kcm |
− kдин |
|
100% |
(16.8) |
|
|
|||||
|
kcm |
+ kдин |
|
|||
|
|
|
|
|
64

7. Сформулюйте та запишіть висновок до роботи. |
|
|
|
|
|
||
Контрольні запитання до лабораторної роботи № 16 |
|
||||||
Гармонічні коливання? Пружинний маятник? Рівняння коливань |
|||||||
пружинного маятника. Статичний і динамічний методи визначення |
|||||||
коефіцієнта жорсткості пружини? Виведення формул для розрахунку |
|||||||
коефіцієнта жорсткості пружини. Графічні методи опрацювання результатів |
|||||||
вимірювань. Метод найменших квадратів. |
|
|
|
|
|
|
|
Лабораторна робота №17 |
|
|
|
|
|||
ДОСЛІДЖЕННЯ МЕХАНІЧНИХ НЕЗАТУХАЮЧИХ КОЛИВАНЬ. |
|
||||||
ВИЗНАЧЕННЯ ВЛАСНОЇ ЧАСТОТИ КОЛИВАНЬ ПРУЖИННОГО |
|||||||
МАЯТНИКА ТА ЖОРСТКОСТІ ЙОГО ПРУЖИНИ |
|
||||||
Мета роботи: визначити |
власну |
частоту |
коливань |
пружинного |
|||
маятника. |
|
|
|
|
|
|
|
Обладнання: штатив з міліметровою шкалою, дві різні пружини, два |
|||||||
вантажі різної маси. |
|
|
|
|
|
|
|
Опис лабораторної установки |
|
|
|
||||
3 |
|
Лабораторна |
|
установка |
|||
|
|
|
|
|
|
|
|
2 |
|
складається |
з штатива 2, що |
||||
4 |
|
|
|
|
|
|
|
|
закріплений на масивній підставці |
||||||
|
|
||||||
L0 |
|
1. До гачків 3, |
вмонтованих |
в |
|||
L |
|
штатив, |
по |
черзі |
підвішують |
на |
|
xст |
|
||||||
|
|
|
|
|
|
|
|
1 |
|
двох різних пружинах два вантажі |
|||||
|
|
|
|
|
|
|
|
5 |
|
з різними |
масами m1 та m2 |
||||
|
|
||||||
|
|
(рис. 17.1). |
Штатив |
оснащено |
|||
Рис. 17.1 |
|
рухомою |
|
|
вимірювальною |
||
лінійкою 4. Для зручності відліку між пружиною та вантажем закріплено |
|||||||
вказівний диск 5 масою m0 . |
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
Короткі теоретичні відомості
Коливальним називається рух, у якому матеріальна точка (або система
точок), багаторазово відхиляється від свого положення рівноваги, щоразу знову повертаючись до нього.
Якщо в коливальній системі не діють сили тертя, то при відсутності зовнішніх сил в ній можуть виникати коливання, які називають вільними (власними). Вільними (власними) називають коливання, що відбуваються в системі, яка надана сама собі після того, як вона була виведена з положення рівноваги. Частота v0 власних коливань системи залежить лише від
властивостей системи та визначається за формулою: |
|
|||||||||
|
|
|
|
v |
|
= |
N |
|
(17.1) |
|
0 |
t |
|||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
де t - час, протягом якого система здійснює N коливань. |
|
|||||||||
|
Якщо власна частота коливань v0 , їх амплітуда A та |
енергія W |
||||||||
залишаються постійними, то коливання називають незатухаючими. |
||||||||||
|
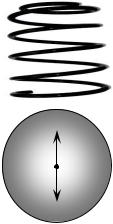
Коливальна система, що складається з невагомої пружини та |
|||||||||
|
|
|
|
прикріпленого до неї вантажу називається пружинним |
||||||
|
|
|
|
маятником (рис. 17.2). |
|
|||||
|
|
|
|
У положенні рівноваги, вага вантажу mg |
||||||
|
|
|
|
врівноважується |
|
силою пружності Fпр , яка, |
за законом |
|||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
|
Гука, становить k |
L , отже: |
|
||||
|
|
|
|
|
||||||
Fпр |
|
|
mg |
= k L |
(17.2) |
mg |
|
|
|||
|
|
|
|
|
|
|
де m - маса вантажу; g - прискорення вільного падіння; |
||||
Рис. 17.2 |
k - коефіцієнт жорсткості |
пружини; |
L - абсолютне |
||
|
|
|
|
|
|
|
видовження пружини. |
|
|
||
З виразу (17.2): |
|
|
|||
|
k = |
mg |
|
|
(17.3) |
|
L |
|
|||
|
|
|
|
||
Частота гармонічних коливань пружинного маятника:
66
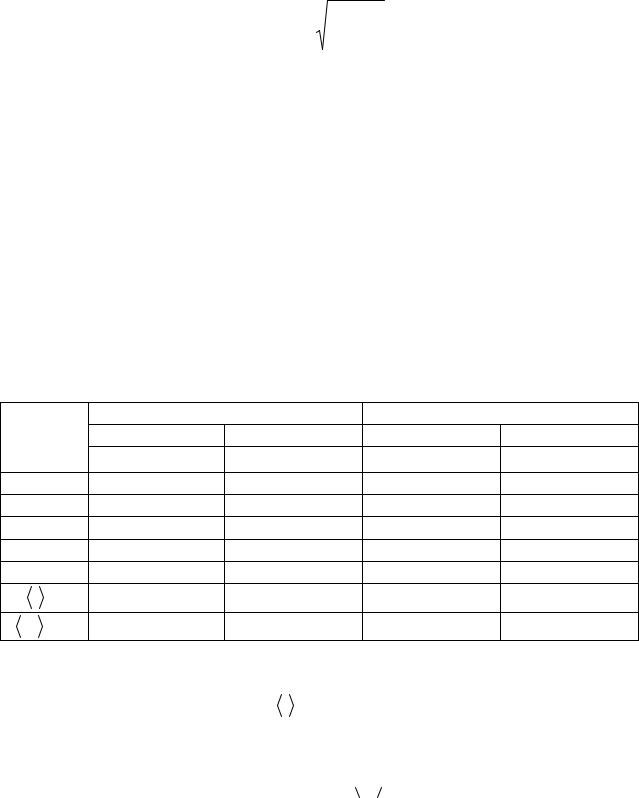
v |
|
= |
1 |
|
k |
|
(17.4) |
0 |
2π |
|
m + m |
0 |
|||
|
|
|
|
||||
|
|
|
|
|
|
|
де m0 – маса вказівного диску.
Порядок виконання роботи
Визначення власної частоти коливань маятника за часом коливань.
1.Відтягніть досліджувану пружину з підвішеним до неї вантажем вниз на 3-4 см та відпустіть її.
2.З допомогою секундоміра виміряйте проміжок часу ti , протягом якого вантаж здійснює N =20 коливань.
3.Повторіть пп. 1-2 не менше 5 разів.
4.Результати вимірювань занесіть до звітної таблиці 17.1.
|
|
|
|
|
Таблиця 17.1 |
|
|
Перша пружина |
Друга пружина |
||
№ п/п |
1-й вантаж |
2-й вантаж |
1-й вантаж |
2-й вантаж |
|
|
|
ti , с |
ti , с |
ti , с |
ti , с |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
t |
, с |
|
|
|
|
v0 |
, Гц |
|
|
|
|
5. Розрахуйте середнє значення часу коливань: |
|
|
|||
|
1 |
n |
|
|
t = |
∑ti , |
(17.6) |
||
|
||||
|
n i=1 |
|
||
де n - кількість значень.
6.За формулою (17.1) розрахуйте частоту  v0
v0  власних коливань маятника.
власних коливань маятника.
7.Повторіть пп. 1-6 для різних пружин та різних важків.
Визначення коефіцієнта жорсткості пружини
1.Переміщуючи по вертикалі лінійку сумістіть її нуль з рівнем, на якому знаходиться вказівний диск.
67
2.Підвісьте до пружини один із важків та визначте видовження пружини
L i за різницею положень вказівного диску відносно шкали лінійки.
3.За виразом (17.3) розрахуйте коефіцієнт жорсткості ki пружини.
4.Виконайте пп. 2-3 для іншого важка.
5.Повторіть пп. 1-4 для іншої пружини.
6.Результати вимірювань та розрахунку занесіть до звітної таблиці 17.2.
|
|
|
|
|
|
|
|
Таблиця 17.2 |
||
Вантаж |
mi |
, кг |
Перша пружина |
Друга пружина |
||||||
, м |
ki , Н/м |
k , Н/м |
L i , м |
ki , Н/м |
k , Н/м |
|||||
|
|
|
L i |
|||||||
|
№ 1 |
|
|
|
|
|
|
|
|
|
|
№ 2 |
|
|
|
|
|
|
|
|
|
7. |
Розрахуйте середні значення коефіцієнтів жорсткості пружин: |
|
||||||||
|
1 |
n |
|
|
k = |
∑ki , |
(17.7) |
||
|
||||
|
n i=1 |
|
||
де n - кількість значень. |
|
|||
Визначення власної частоти коливань |
маятників за значеннями |
|||
коефіцієнтів жорсткості пружин
1.Користуючись даними таблиці 17.2 та виразом (17.4) розрахуйте значення власних частот  v0
v0  коливань маятників та внесіть отримані результати до звітної таблиці 17.3.
коливань маятників та внесіть отримані результати до звітної таблиці 17.3.
|
|
|
|
|
Таблиця 17.3 |
|
|
|
|
|
|
|
|
Вантаж |
mi |
+ m0 |
, кг |
v0 |
, Гц |
|
|
|
|||||
Перша пружина |
Друга пружина |
|||||
|
|
|
|
1-й вантаж
2-й вантаж
2.Порівняйте отримані значення власних частот коливань маятників, сформулюйте та запишіть висновок до роботи.
Контрольні запитання до лабораторної роботи № 17
Пружинний маятник. Рівняння коливань пружинного маятника. Закон
Гука. Енергія коливань. Додавання гармонічних коливань. Резонанс. Правила
округлень результатів розрахунку.
68
|
|
Лабораторна робота №18 |
|
|
|
||||
|
ВИЗНАЧЕННЯ СИЛИ ВЗАЄМОДІЇ ДВОХ ТІЛ ПРИ ЇХ |
||||||||
|
|
ПРУЖНОМУ ЗІТКНЕННІ |
|
|
|
||||
|
Мета роботи: визначити середню силу взаємодії двох кульок при їх |
||||||||
|
|
пружному ударі. |
|
|
|
|
|
|
|
|
Обладнання: лабораторна установка, що складається з двох |
||||||||
|
|
підвішених на нитках кульок, електромагніту, шкали |
|||||||
|
|
для відліку кутів та електронного секундоміра. |
|
||||||
|
|
Опис лабораторної установки |
|
|
|||||
|
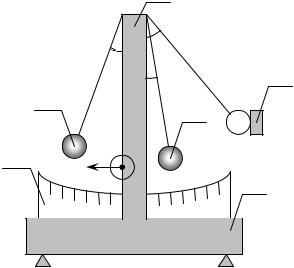
Схема лабораторної установки зображена на рис 18.1. На вертикальній |
||||||||
|
|
1 |
|
стійці |
(1), |
яка |
закріплена на |
основі |
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 |
|
(2), на |
тонких |
нерозтяжних |
нитках |
||
|
α2′ |
|
висять |
дві кулі (3) |
і (4). |
Якщо |
|||
|
|
|
|||||||
|
α1′ |
6 |
відвести вбік праву кулю на кут α1 |
||||||
|
|
||||||||
|
4 |
|
|
||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
(до електромагніту (6)) і відпустити |
||||||
|
|
|
|
||||||
|
R |
|
|
|
|
|
|
|
|
5 |
u2 |
|
|
її, то вона зіткнеться з лівою кулею і |
|||||
|
|
2 |
|
кулі розлетяться відповідно на кути |
|||||
|
|
|
|
α1′ та α2′ . |
|
|
|
|
|
|
|
|
|
В даній роботі імпульс другої |
|||||
|
Рис. 18.1 |
|
кулі до зіткнення p2 =0, оскільки до |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
удару |
її |
швидкість |
υ2 =0. |
Таким |
|
чином, зміна імпульсу другої кулі за час удару буде дорівнювати її імпульсу |
|||||||||
на кінець взаємодії з першою. |
|
|
|
|
|
|
|
||
Короткі теоретичні відомості
Якщо на тіло діє протягом деякого часу τ сила F , то імпульс тіла змінюється як за напрямком, так і за значенням. Виходячи з другого закону Ньютона можемо записати:
R |
|
R |
|
= |
p |
|
|
F |
(18.1) |
||
|
|
τ |
|
69

де p = p′ − p0 - зміна імпульсу тіла за час взаємодії; p′ та p0 - відповідно кінцеве та початкове значення імпульсів тіла.
Значення середньої сили взаємодії F між кульками під час їх прямого центрального пружного зіткнення можна розрахувати за формулою:
F = p′ − p0 (18.2)
τ
де p′ = mu - імпульс кульки до удару; m - маса кульки; u - швидкість кульки після удару; p0 = mυ0 - імпульс кульки до удару; υ0 - швидкість кульки до удару.
Якщо першу кулю відхилити на кут α1 і відпустити, то вона почне падати і зіткнеться в нижньому положенні з другою. Далі, друга куля, маючи
початкову швидкість u |
|
та кінетичну енергію W |
= |
m2u22 |
почне підійматись |
2 |
|
||||
|
к2 |
2 |
|
||
|
|
|
|
||
(m2 - маса другої кульки). За законом збереження енергії, для моменту
максимального відхилення нитки з другою кулею (що відповідає максимальній висоті підняття кулі), можна стверджувати, що її кінетична енергія повністю перейшла в потенціальну. Так, враховуючи геометрію задачі, неважко показати, що потенціальна енергія другої кульки дорівнюватиме при максимальному відхиленні становитиме:
Wп2 = m2 gL(1− cosα2′ ) |
(18.3) |
де g – прискорення вільного падіння на Землі; L - довжина нитки підвісу.
Прирівнюючи між собою Wп2 і Wк2 (у відповідності з законом
збереження енергії), виразимо швидкість другої кулі після удару: |
|
|||||
|
|
= 2 |
|
|
sin α2′ |
|
u |
2 |
|
gL |
(18.4) |
||
|
|
2 |
|
|||
|
|
|
|
|||
Імпульс другої кулі безпосередньо після удару: |
|
|||||
|
|
p′2 |
= m2u2 |
(18.5) |
||
При цьому масу другої кульки необхідно визначати за відповідною довідковою таблицею.
Користуючись виразом (18.2) та згідно вище сказаному, запишемо:
70
