Методичні вказівки містять розв’язки типових задач і варіанти індивідуальних завдань з курсу теорії функцій комплексної змінної.

1 – Алгебра комплексних чисел;

2 – Елементарні транциндентні функції комплексних змінних;

3 – Дифференціювання(!) функції комплексної змінної;

4 – Інтегрування функцій комплексної змінної;

5 – Ряди Лорана і Тейлора;

6 – Застосування лишків(!) до обчислення інтегралів;

7 – Комфортні відображення лінійних, дробово-лінійних, і основних елементарних функцій;(!)

1. Комплексні числа і дії над ними.

Числа (потрібен чи не потрібен абзац?) виду , де, називаються комплексними.

- дійсна частина комплексного числа;

- уявна частина комплексного числа;

Комплексне число в деякій Декартові системі координат зображується точкоюз координатамиабо радіус-вектором точки (мал.1). Із геометричного змісту комплексного числа (мал.1) зрозуміло, що(1) або(2)

Мал.1

(1)- тригонометрична форма комплексного числа

(2)- експоненціальна форма комплексного числа

- модуль комплексного числа, а - аргумент, де();-головний кут і;().називається комплексно-спряженим числом.

Дії над комплексними числами:

Нехай і, тоді:

1. , якщоі()

2. (!)

3. (!)

4. , має місце формула Муавра:(!) ;(по поводу чего в методичке написано????)

5. , або , k=0,1,2,… , (n-1).

Приклади: виконати указані дії, якщо (z=2+5i):

1)2)3)4)

5)6) (В методичке другое) 7)8)

9)10)11)

Розв’язки

1)

Радіус-вектор дорівнює сумі двох радіус-векторівта(мал. 2).

Мал. 2

2)

Радіус-вектор дорівнює сумі радіус-векторівта(мал. 3).

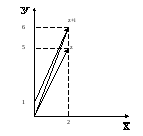
Мал. 3

3)

Радіус-вектор дорівнює сумі радіус-векторівта(мал.4).

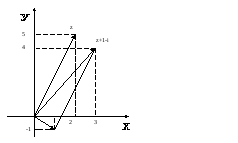
Мал. 4

4);або за формулою Мавра

(була помилка)

; k є Z.

5)

6)(не зрозуміла помилка)

7)або

Маємо:

; =

Або:

8);

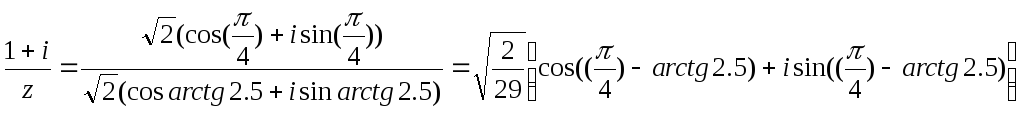
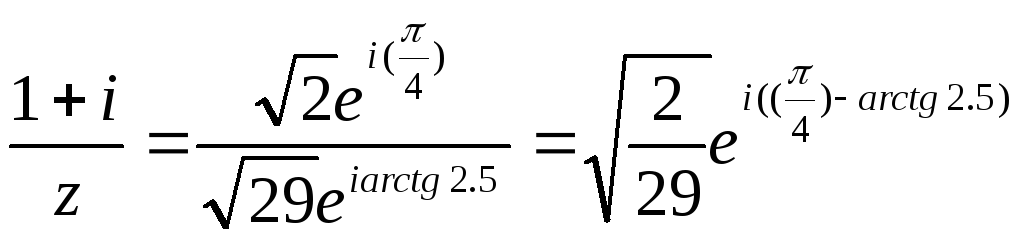
9)(в останньому не зрозуміло, під корнем весь вираз чи тільки «2-ійка»)

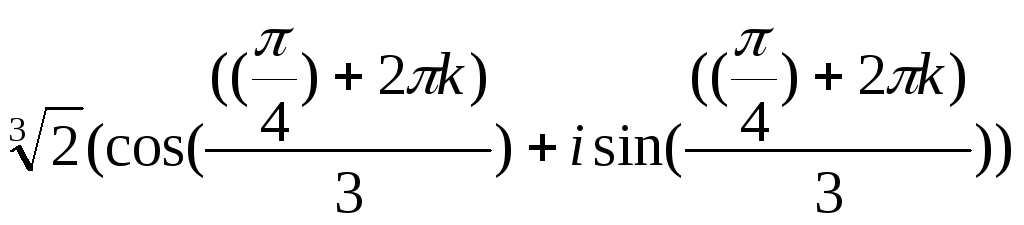, k=0,1,2

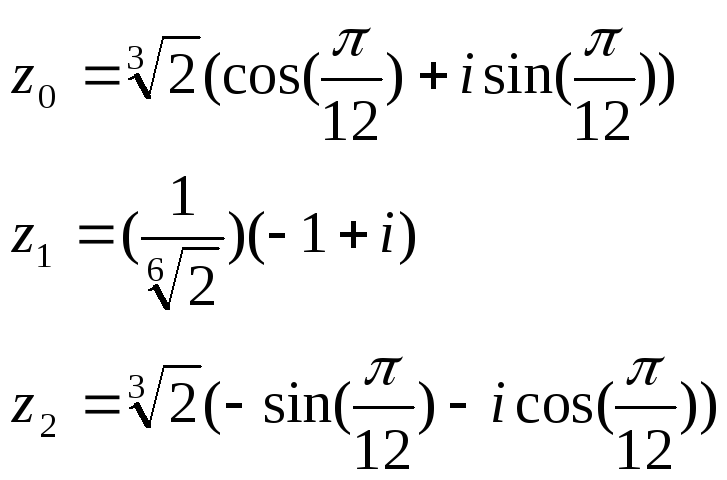
10),k=0,1

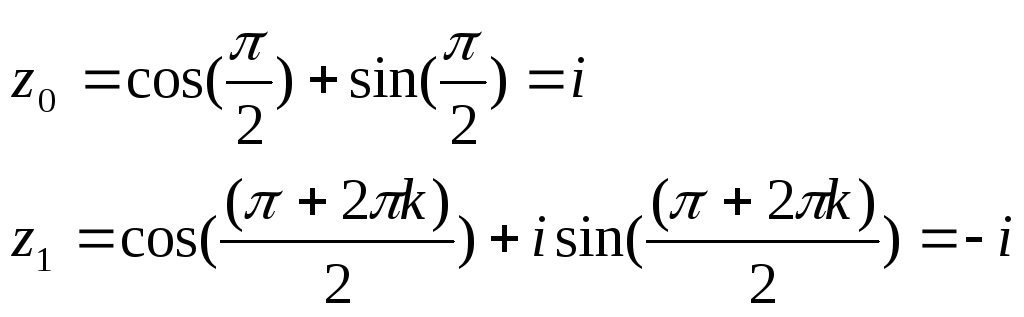
11)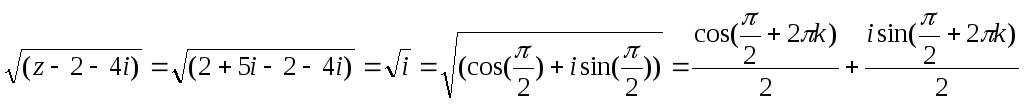k=0,1

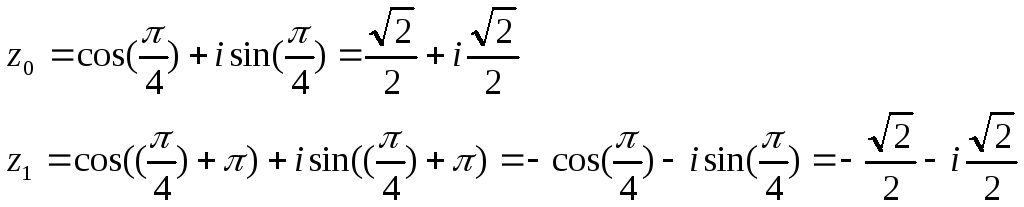
Приклади

В площині зобразити геометричні місця точок для заданих співвідношень:

1);;;

2);,,

3);,;

4)

5), ,

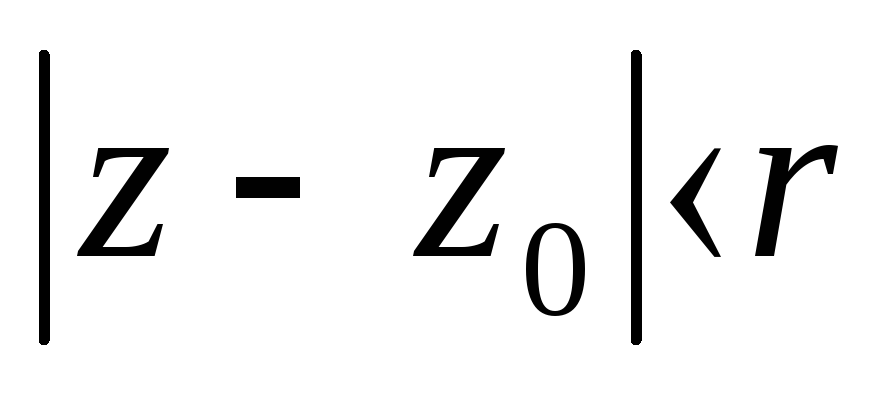Розв’язки:

1). Маємо:,

Тоді ,(В методичці на початку рів-ня опечатка, або так потрібно(порядковий номер “Y”… і в ньому стоїть знак додавання))

Звідси випливає, що ,,- параметричні рівняння кола радіусаз центром в точці (), (мал. 5)

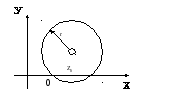
Мал. 5

Маємо ;,(<=Повторюється...!)

- параметричні рівняння прямої

Включаючи параметр , маємо:т,(мал. 6)

Мал. 6 Мал. 7

3) З ,, випливає, що векторитаколінеарні.

Геометричне місце точок є пряма , що проходить через точкиі(мал. 7)

4) Модуль різниці двох комплексних чисел в площинідорівнює відстані між точкамиі, томує сума відстаней довільної точкивід двох точокіі дорівнює 5. Отже, геометричне місце точокє еліпс з фокусами в точкахі, велика вісь еліпса дорівнює 5 (мал. 5)

5) Оскільки дорівнює відстані між точкамиітоє геометричне місце точок, відстань яких до даної точкименше за, тобто коло радіусає центром в точці(мал. 9).

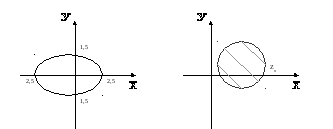
(в методичці є незрозумілості в обох малюнках) Мал. 8 Мал. 9

2. Елементарні функції комплексної змінної.

Відображення(потрібен чи не потрібен абзац?) , яке кожному комплексному числу(потрібно чи ні ставити скобки в D) ставити у відповідність деяке комплексне число , називається функцією комплексної змінної і записується так:.

Функція комплексної змінної може бути многозначною. В деякому випадку при відображенні кожному комплексному числувідповідає не одне , а декілька значень комплексної змінної. Нехай,. Тоді залежністьміж комплексними зміннимиірівносильна двом залежностям дійсних функційівід дійсних зміннихі:і.(може бути не зв’язка в методичці)

До основних елементарних функцій комплексної змінної відносяться:

1. Дробово-раціональна функція:

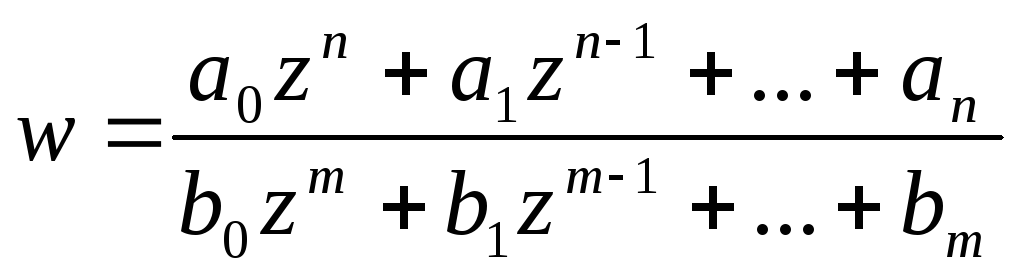,(як я це зрозумів з методички)

2. Експоненціальна показникові функція:

При цьому і()(кома пісня двійки),

тобто функція - періодична,

3. Тригонометричні функції:

;

;

Ці функції періодичні з періодом . При цьому має місце формула Ейлера:.

4. Гіперболічні функції:

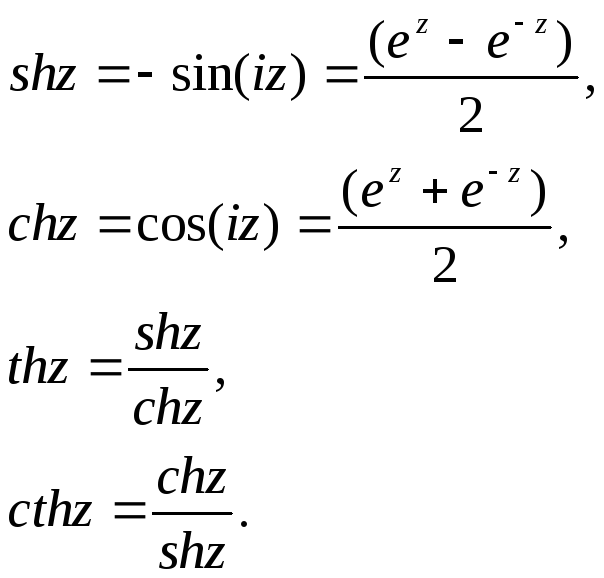
5. Логарифмічна функція ,, визначається, як функція, зворотня до показникової:().

Ця функція багатозначна.

- головне значення(при). При цьому:

().

6. Зворотні тригонометричні функції ,,,.

Всі ці функції багатозначні і визначаються через логарифм за формулами:

(не зрозуміло про логарифм, де він стоїть).

7. Зворотні гіперболічні функції ,,,,визначаються за формулами:

,

,

,

.

Приклади:

Обчислити:

1) ; 2); 3)

Розв’язки:

1) З формули маємо

2) З формули ,.

Маємо

3) .

Розв’язати рівняння ,

Маємо:

;