11. Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.

Ба́зис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.

Определение. Два вектора называются ортогональными, если угол междуними равен прямому углу, т.е. .

Обозначение:  – векторы  и  ортогональны.

Определение. Тройка векторов  называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. , .

Определение. Тройка векторов  называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .

Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.

Определение. Упорядоченная некомпланарная тройка векторов , отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора  на плоскость, в которой лежат первые два вектора  и , кратчайший поворот первого вектора  ко второму  происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).

Здесь, на изображена правая тройка векторов . На следующем рис.7  изображена левая тройка векторов :

Определение. Базис  векторного пространства  называется ортонормированным, если  ортонормированная тройка векторов.Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом , см. следующий рисунок:

Любой вектор можно разложить по этому базису:

.

- координаты базиса.

12. Скалярное произведение. Координатная форма скалярного произведения.

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярным произведением в векторном пространстве над полем называется функция для элементов , принимающая значения в , определенная для каждой пары элементов и удовлетворяющая следующим условиям:

1. для любых трех элементов и пространства и любых чисел справедливо равенство (линейность скалярного произведения по первому аргументу);

2. для любых и справедливо равенство 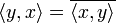, где черта означает комплексное сопряжение (эрмитова симметричность);

3. для любого имеем , причем только при (положительная определенность скалярного произведения).

Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.

Заметим, что из п.2 определения следует, что действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.