Вопрос7. Теорема Кронекера-Капелли о совместности системы лау.

Пусть дана матрица общего вида порядка m  n:

А=.

Обозначим строки матрицы через ,,…,:=,=, …,=

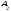Пусть: =,; =

Тогда сумма ++…+,, будет наз. линейной комбинацией строк () м-цы А.

Если сущ-ют числа ,такие что=++…+++...+, то говорят, что строкавыражается ч-з остальные строки,, …,,, …,. Строки,, …,наз-сялинейно зависимыми, если существуют числа

, не все одновременно равные нулю, что ++…+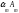=0, где 0=(0 0 …0). Если же данное равенство выполняется лишь когда все числа=0,, то говорят, что строки,,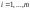линейно независимы. Заметим, что, если строки линейно зависимы, то, по крайней мере, одна из них выражается ч-з остальные. Если же строки линейно независимы, то ни одна строка не выражается ч-з остальные. Аналогично вводится понятие линейной зависимости и независимости столбцов.

Для того, чтобы система линейных алгебраических уравнений была совместной (то есть имела решение), необходимо и достаточно, чтобы ранг исходной матрицы системы совпадал с рангом расширенной матрицы, то есть r(A) = r(С).

1)если r(A) = r(С)= n, где n – число неизвестных системы, то данная система имеет единственное решение;

2)если r(A) = r(С) = k < n, то система имеет бесконечное множество решений;

3)если r(A) ≠ r(С), то система несовместна, то есть не имеет решений.

Если число неизвестных > числа урав-й, то сис-ма либо не имеет реш-й, либо имеет их бесконечное множ-во (если r(A)=r(С)=k <n.)

Вопрос 8. Формулы Крамера решения систем лау.

Рассмотрим еще один метод решения системы (1)

Пусть, как и ранее, n = m.

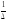
Тогда из формулы (3) имеем: Х=× В ==_{. (4)}

В формуле (4) = det A – главный определитель системы (1),

(разлагаем по j-му столбцу)=;, – побочные опред-ли сис-мы (1).

Они получаются из главного определителя заменой соответствующего j-го столбца столбцом свободных членов. Формулы (4) называются формулами Крамера.

1.Для матрицы А системы уравнений вычислить ее главный определитель = det A.

2.Последовательно,заменяя каждый столбец м-цы А столбцом свободных членов, получить побочные опред-ли ,

3. а)Если ≠ 0, то по формулам (4) определить единственное решение системы (1):,, ….,.

б) Если =0, а хотя бы один из побочных опред-лей≠0, то исходная сис-ма (1) несовместна, т. е. не имеет решений

в) Если == 0,, то исходная система (1) имеет бесконечное множество решений.

Вопрос 9 Метод Гаусса решения систем лау.

Метод Гаусса применим к любой сис-ме ЛАУ. Иногда этот м-д наз-ют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.

Итак, пусть задана система m ЛАУс n неизвестными: (6)

В матрич-м виде сис-ма (6) запис-ся АХ=В, где А – прямоуг-я м-ца размера mn: А=, а ,

Х и В – м-цы-столбцы: Х=,В=.

Если в рез-те преобраз-й м-цы сис-мы получ-я треуг-я м-ца, то сис-ма будет иметь вид:

где

Из последнего урав-я можно найти , а затем, подставляя найденноев предпоследнее урав-е, найтии т.д. В итоге будем иметьединственное решение ,, …,. В этом случае ранг матрицыА системы уравнений равен n.

Если в рез-те преобраз-й м-цы сис-мы получится трапециевид-я м-ца, то сис-ма примет вид:

где

В этом случае k<n, следоват-но, сис-ма урав-й будет неопределенной, т. е. будет иметь бесконечное множество решений, т. к. она содержит n – k свободных переменных:

Придавая свободным переменным ,, …,произвольные значения, будем иметь каждый раз новое реш-е исходной сис-мы урав-й, т.е. реш-й будет бесконечное множ-во. В этом случае ранг матрицы А системы равенk.

Если в рез-те преобразований получено урав-е, в кот. коэф-ты при всех неизвестных = 0, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.

Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициенты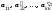отличны от нуля. Если же какой-либо из этих коэф-в = 0, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.

Метод Гаусса применяется и для однородных систем ЛАУ. В этом случае, если получаем треугольный вид сис-мы урав-й, то она будет иметь единственное (нулевое) решение _{== …==} 0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.

При решении системы ЛАУметодом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.