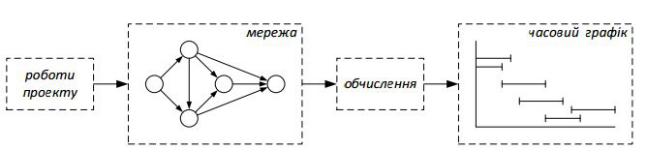
наведено основні етапи реалізації цих методів. На першому етапі визначаються окремі роботи, що входять в проект, їхня послідовність та тривалість. Далі проект подається у вигляді мережі, де графічно зображено послідовність робіт

проекту. На третьому етапі на основі побудованої мереж виконуються обчислення, в результаті яких складається часовий графік реалізації проекту.

Рис. 3.1. Основні етапи виконання методів CPM та PERT

3.4. Побудова мережі проекту

3.4.1 Правила побудови мережі проекту.

На мережевому графіку події зображуються вершинами, роботи – орієнтованими дугами.

При побудові мережі проекту необхідно дотримуватись таких правил:

1)в мережі, крім завершальної події, не повинно бути тупикових подій, з яких не виходить жодна робота;

2)в мережі, крім вихідної події, не повинно бути хвостових подій, яким не передує жодна робота;

3)в мережі не повинно бути замкнутих контурів (циклів) та петель;

4)будь-які дві події повинні бути зв’язані лише однією роботою;

5)в мережі повинні бути лише одна вихідна та одна завершальна події.

Наявність в мережі тупикових та хвостових подій, а також циклів вказує на необхідність проведення більш ретельного аналізу робіт та взаємозв’язків між ними. Якщо в проекті потрібно виконати декілька робіт при одних і тих же початковій та кінцевій подіях, то в таких випадках необхідно ввести фіктивні події та роботи.

Графічно правила побудови мережі наведено на рис. 1.3.

Якщо процес реально можна почати або завершити з кількох робіт, то необхідно ввести фіктивні вихідну та завершальну події.

26

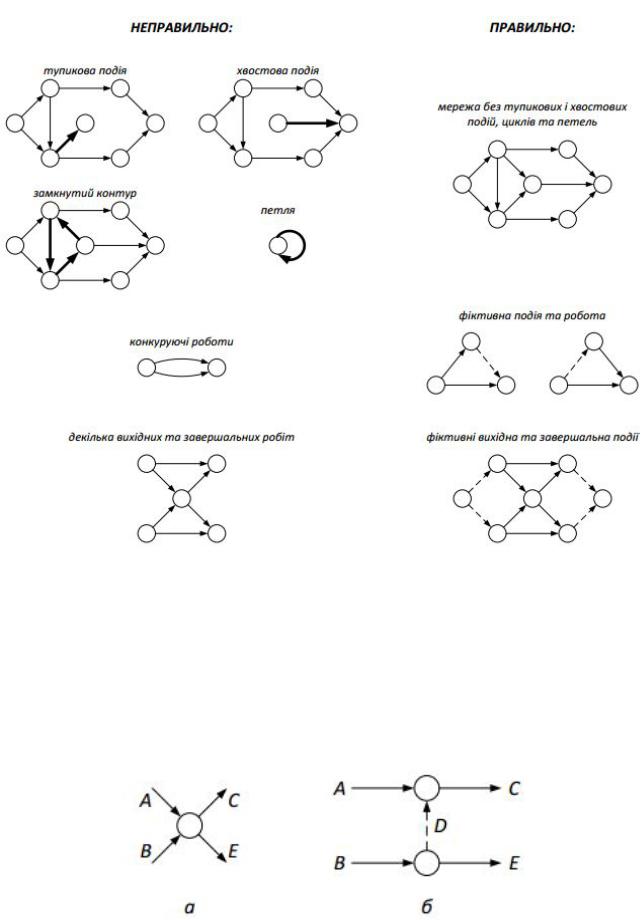
Рис. 3.2. Правила побудови мережі проекту

Припустимо, що чотири роботи повинні задовольняти таким правилам:

-робота С повинна початись одразу після завершення робіт А і В;

-робота Е повинна початись одразу після завершення роботи В.

На рис. 1.4, а наведено неправильно зображення робіт, оскільки виходить, що робота Е повинна початись як після завершення як роботи В, так і роботи А. На рис. 1.4, б наведено, як за допомогою фіктивної роботиD вирішити цю проблему.

27

Рис. 3.3. Використання фіктивної роботи для правильного відображення послідовності робіт

Вершини мережі можна нумерувати довільно, але для розв’язування задач зручно використовувати так звану правильну нумерацію подій– нумерація події, за якої номер кожної наступної події більший, ніж номер будь-якої попередньої.

3.4.2 Метод CPM.

Метод СРМ передбачає, що тривалість виконання кожної роботи є відома.

Врезультаті використання методу СРМ можна визначити:

-мінімальний час виконання проекту;

-множину критичних та некритичних робіт;

-час початку та закінчення виконання окремих робіт.

називаються критичними.

Всі події характеризуються:

-раннім терміном настання події – Еі;

-пізнім терміном настання події – Lі.

j ).

Для критичної роботи (i , j ) виконуються умови:

-E i = L i ;

-E j = L j ;

-L i - L j = E j - E i = t i j

28

без збільшення тривалості проекту. Критичні роботи резерву часу не мають.

Визначення критичного шляху та часових параметрів мережевого графіка виконують в два проходи. При проході вперед визначаються ранні терміни настання подій, при проході назад – пізні терміни настання тих же подій.

Через це мережевий графік хоч і дає уявлення про порядок виконання робіт, але недостатньо наглядний для визначення робіт, які виконуються в кожен момент

довжина якого рівна тривалості роботи.

29