- •Міністерство освіти і науки україни
- •Вища математика Модуль 5 Кратні та криволінійні інтеграли
- •Література
- •Кратні та криволінійні інтеграли
- •Подвійний інтеграл Основні поняття та теореми
- •Двовимірний Евклідів простір
- •Область в Евклідовому просторі
- •Інтегральна сума
- •Подвійний інтеграл
- •Властивості подвійних інтегралів
- •Зміна порядку інтегрування
- •Кожен з подвійних інтегралів заміняють на повторний інтеграл:
- •Застосування подвійних інтегралів.
- •Розглянемо деякі приклади застосування подвійного інтеграла.
- •Маса неоднорідної пластини.
- •Приклади розв’язання задач Приклад 1.1
- •Розв’язання
- •Приклад 1.2
- •Розв’язання
- •Приклад 1.3
- •Розв’язання
- •Приклад 1.4
- •Розв’язання
- •Приклад 1.5
- •Розв’язання
- •Область .
- •Область .
- •Приклад 1.6
- •Розв’язання
- •1.3. Тести для перевірки
Приклад 1.4
Обчислити
подвійний інтеграл від функції
![]() по області
по області![]() .
Побудувати область інтегрування.
Обчислити інтеграл при різному порядку
інтегрування.
.
Побудувати область інтегрування.
Обчислити інтеграл при різному порядку
інтегрування.
Розв’язання
Крок 1. Побудуємо область інтегрування. Перевіримо виконання достатніх умов існування подвійного інтеграла.
|
|
1. Областю інтегрування є прямокутник. Це квадровна область.
2.
Підінтегральна функція
Область інтегрування є правильною в напряму обох осей. |
Обчислимо подвійний інтеграл, проводячи заміну на повторний спочатку в напряму осі ОУ, а потім у напряму осі ОХ.
Варіант 1
Крок 1.1. Складемо подвійний інтеграл:
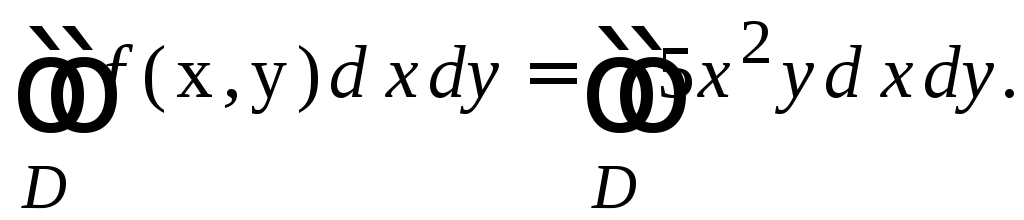
Крок 1.2. Замінимо його на повторний інтеграл, враховуючи, що область інтегрування є правильною в напряму осі ОУ:
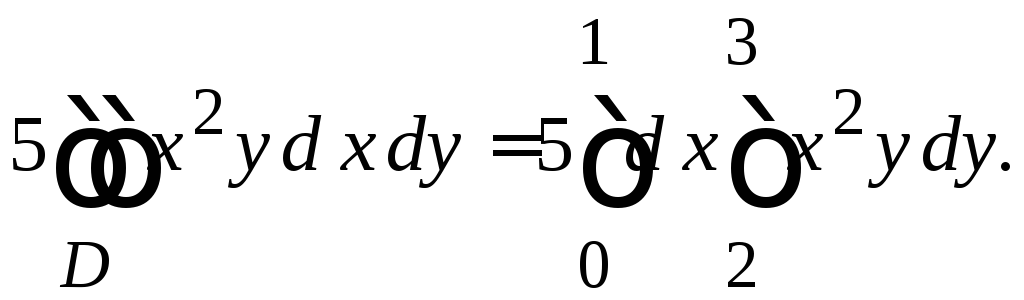
Крок 1.3. Обчислимо внутрішній інтеграл:
 .
.
Крок 1.4. Підставимо знайдену функцію у зовнішній інтеграл і обчислимо його,
 .
.
Крок
1.5. Обчислимо
подвійний інтеграл від функції
![]() :
:
 .
.
Варіант 2
Обчислимо інтеграл, змінивши порядок інтегрування.
Крок 2.1. Складемо подвійний інтеграл:
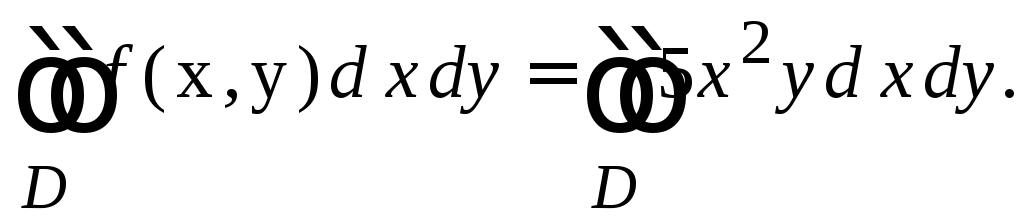
Крок 2.2. Замінимо його на повторний інтеграл, враховуючи, що область інтегрування є правильною в напряму осі ОХ:

Крок 2. 3. Обчислимо внутрішній інтеграл:
 .
.
Крок 2.4. Підставимо знайдену функцію у зовнішній інтеграл і обчислимо його,
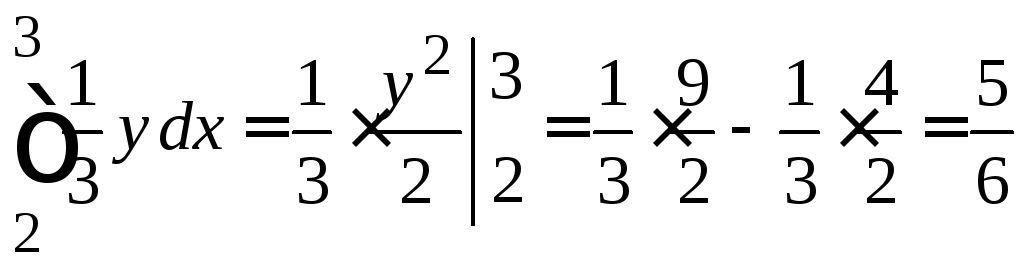 .
.
Крок
2.5. Обчислимо
подвійний інтеграл від функції
![]() :
:
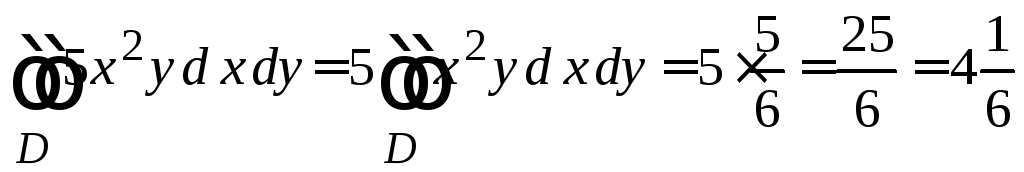 .
.
Таким чином, бачимо, що значення інтеграла не залежить від порядку інтегрування.
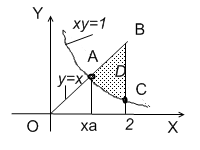
Приклад 1.5
Обчислити
площу області D,
яка обмежена прямими
![]() ,
,![]() і гіперболою
і гіперболою![]() ,
якщо
,
якщо![]() та
та![]() .
Обчислення виконати, для повторних
інтегралів, взятих у різних напрямах.
.
Обчислення виконати, для повторних
інтегралів, взятих у різних напрямах.
Розв’язання
Крок 1. Побудуємо область інтегрування. Перевіримо виконання умов існування подвійного інтеграла.
|
|
|
З рисунку видно, що ця область є правильною в напряму обох осей.
Крок 2. Знайдемо кутові точки області інтегрування. Область має три кутові точки:
– точка
В
перетину прямих
![]() та
та![]() ;
її координати
;
її координати![]() ;
;
– точка
С
перетину прямої
![]() і гіперболи
і гіперболи![]() ;
її координати
;
її координати ;
;
– точка
А
перетину
прямої
![]() і гіперболи
і гіперболи![]() .
.
Знайдемо координати точки А, розв’язавши систему
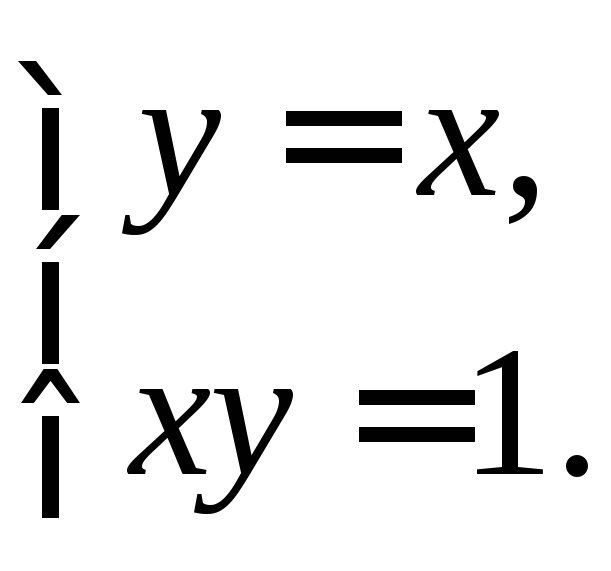
Підставимо
значення невідомого у
з першого рівняння в друге, одержимо
рівняння
з невідомим
![]() :
:
![]() .
.
Рівняння
має два корені:
![]() ,
,![]() .
Виходячи з умови задачі
.
Виходячи з умови задачі![]() ,
вибираємо додатний корінь
,
вибираємо додатний корінь![]() .
.
Знайдемо
ординату кутової точки А.
Підставимо значення
![]() у рівняння
у рівняння![]() ,
одержимо
,
одержимо![]() .
.
Кутові
точки області інтегрування мають
координати
![]() ,
,![]() ,
, .
.
Варіант 1
Крок 1.3. Область інтегрування D є правильною в напряму осі ОУ. Опишемо її аналітично за допомогою системи нерівностей.
Інтервал
зміни значень змінної х
встановимо у відповідності до значень
абсцис кутових точок
![]() і
і області інтегрування.
області інтегрування.
Значення
змінної у
в межах області інтегрування D
обмежені знизу величинами ординат
точок, які належать гіперболі
![]() (нижня межа), а зверху величинами ординат
точок, які належать прямій
(нижня межа), а зверху величинами ординат
точок, які належать прямій![]() (верхня
межа).
(верхня
межа).
D:
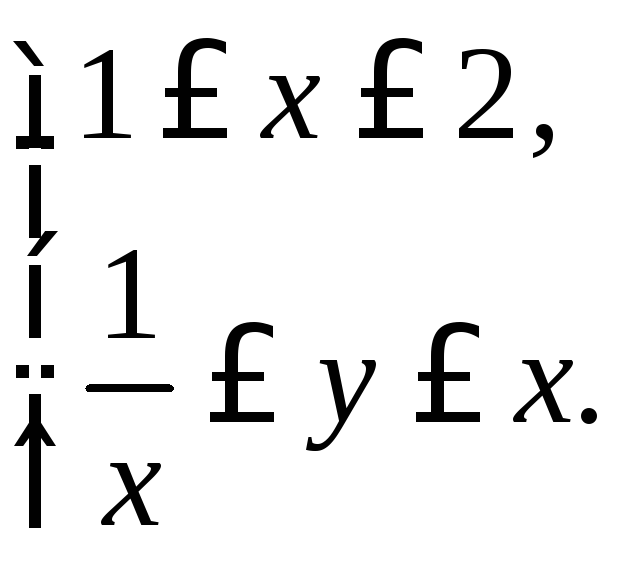
Крок 1.4. Запишемо подвійний інтеграл через повторний інтеграл, скориставшись аналітичним описом області інтегрування:
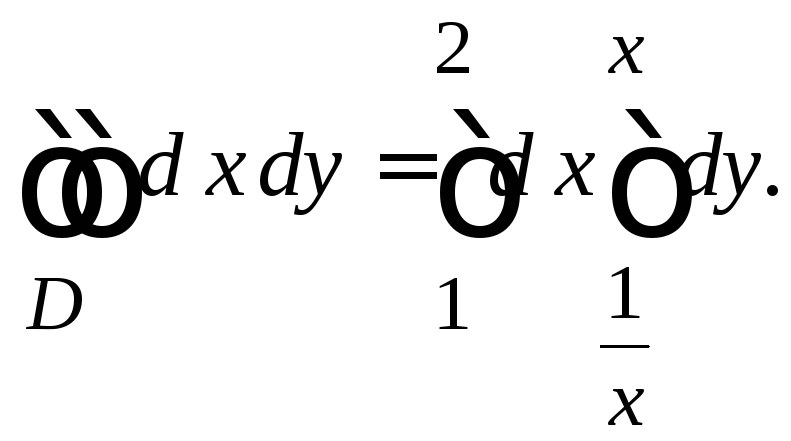
Крок 1.5. Обчислимо внутрішній інтеграл:
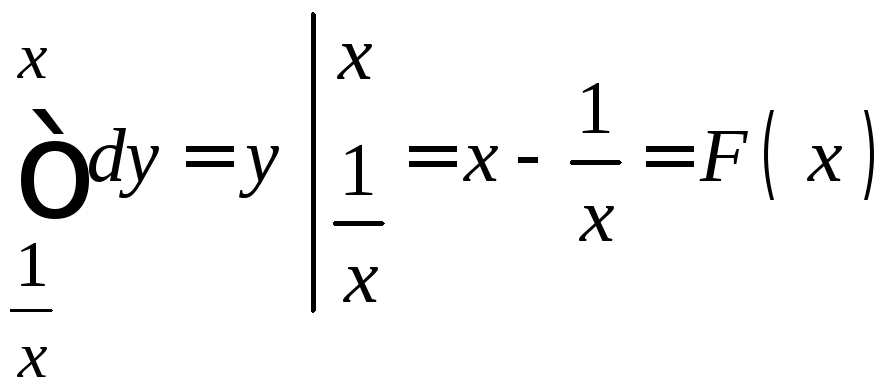
Крок 1.6. Підставимо знайдену функцію у зовнішній інтеграл і обчислимо його,
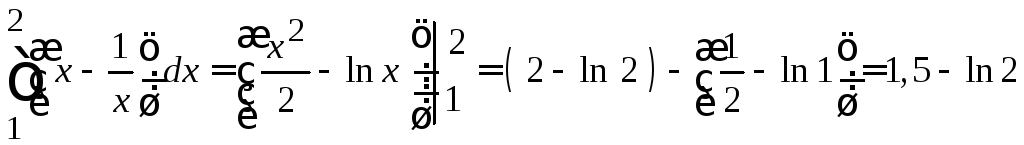 .
.
Площа
області інтегрування дорівнює
![]() .
.
Обчислимо подвійний інтеграл, змінивши порядок інтегрування.
Варіант 2
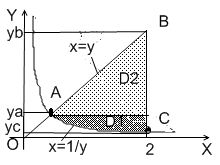
Крок 2.3. Область інтегрування D є правильною в напрямі осі ОХ.
|
|
Але
її нижня межа складається з двох
ланцюгів: перший належить гіперболі
|
Опишемо кожну частину розбиття область інтегрування D аналітично за допомогою систем нерівностей.
Розглянемо область
 .
.
Інтервал
зміни значень змінної у
встановимо у відповідності до значень
ординат кутових точок
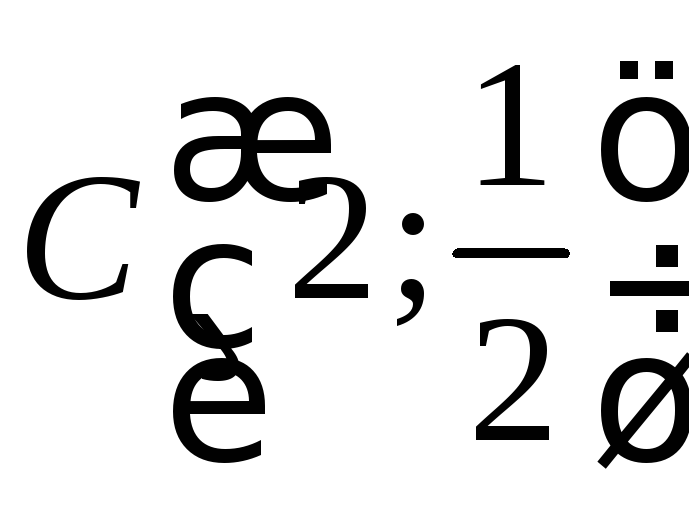 і
і![]() області інтегрування.
області інтегрування.
Значення
змінної х
в межах області
![]() обмежені знизу величинами абсцис точок,
які належать гіперболі
обмежені знизу величинами абсцис точок,
які належать гіперболі![]() (нижня межа), а зверху величинами абсцис
точок, які належать прямій
(нижня межа), а зверху величинами абсцис
точок, які належать прямій![]() (верхня
межа).
(верхня
межа).
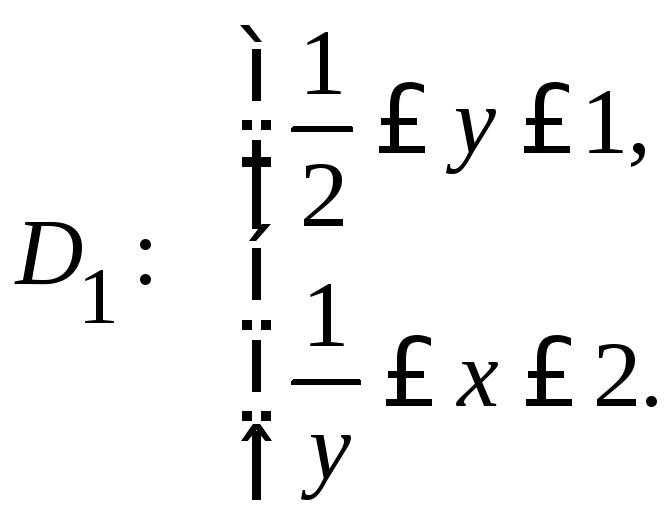 .
.
Розглянемо область
 .
.
Інтервал
зміни значень змінної у
встановимо у відповідності до значень
ординат кутових точок
![]() і
і![]() області інтегрування.
області інтегрування.
Значення
змінної х
в межах області
![]() обмежені знизу величинами абсцис точок,
які належать прямій
обмежені знизу величинами абсцис точок,
які належать прямій![]() (нижня межа), а зверху величинами абсцис
точок, які належать прямій
(нижня межа), а зверху величинами абсцис
точок, які належать прямій![]() (верхня
межа).
(верхня
межа).
 .
.
Крок 2.4. Складемо подвійний інтеграл:
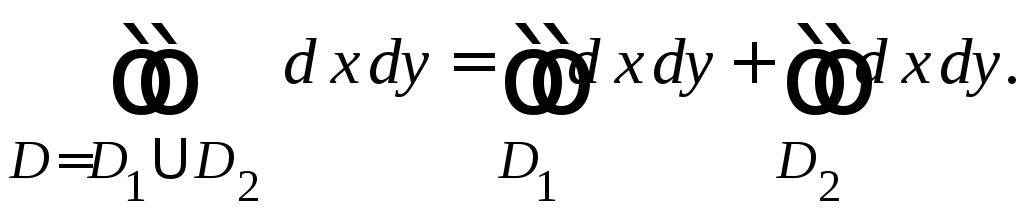
Крок 2.5. Запишемо подвійний інтеграл через повторні інтеграли, скориставшись аналітичним описом області інтегрування. Для кожної частини розбиття виконаємо окремо перехід від подвійного інтеграла до повторного.