Інтегральна сума

Розв’язання багатьох практичних задач пов’язано з обчисленням значення деякої величини F, закон зміни якої невідомий, але відома функція f, яка певним чином характеризує цей змінний процес в точках заданої області D. Значення невідомої величини F залежать від заданої функції f та від вибору області D.

Наприклад. Для однорідної пластини її маса пропорційна площі пластини, оскільки чисельне значення об’єму пластини відрізняється від чисельного значення її площі на нескінченно малу величину, тобто ,,. Якщо ж обчислити за розглянутими формуламимасу неоднорідної пластини, то одержаний результат буде мати велику похибку. Тому необхідно шукати інший спосіб обчислення маси неоднорідної пластини.

Геометрію пластини опишемо аналітично як деяку область D площини ХОУ. Закон зміни густини в межах області D відомий, . Значення маси неоднорідної пластини обчислюють яксукупну величину в точках області D. Для знаходження маси будують математичну модель, в основу якої покладена ідея складання інтегральної суми. Математичні моделі складаються в двовимірному Евклідовому просторі.

При побудові математичної моделі наближене значення шуканої величини F в області D визначають як суму нескінченно малих величин. Це дозволяє зменшити похибку обчислень. Точне значення шуканої величини F відповідає границі послідовності її наближених значень, одержаних при різних способах формування інтегральних сум.

Побудова математичної моделі

Розглянемо в декартовій площині ХОУ квадровну область D, в точках якої визначена функція двох змінних, .

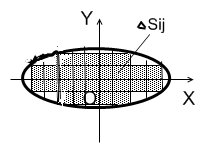
1. Розглянемо область D.

Рис. 1.4

Розіб’ємо довільним чином область D на частин,, якіне мають спільних внутрішніх точок, і їх площі дорівнюють ,.

Площа області D дорівнює сумі таких площ . Якщо кількість частин розбиття збільшувати,, то навіть площа найбільшої з одержаних частин розбиття стає нескінченно малою величиною,,

2. Будемо вважати, що для кожної частини розбиття в різних її точках значення функції відрізняються на нескінченно малі величини, які мають порядок малості більший за порядок малості площі частини розбиття. Тобто, можна вважати, що функціяв точках частини розбиттяє “ практично “ сталою. Тому у кожній частині розбиттявиберемо довільну точку, в якій обчислимо значенні функції.

3. Знайдемо наближене значення шуканої величини в частині розбиття. Будемо вважати, що це значення пропорційне площічистини розбиття. Коефіцієнт пропорційності дорівнює значенню функціїу вибраній точці,. Таким чином, в межах частини розбиття значення шуканої величининаближено дорівнює добутку сталої на нескінченно малу величину, , і є нескінченно малою величиною,, порядок малості якої відповідає порядку малості площі частини розбиття.

4. Утворимо суму із наближених значень шуканої величини в частинах розбиття :

. (1.2)

Таку суму називають інтегральної сумою функції , якавідповідає заданому розбиттю області D та заданому вибору проміжних точоку частинах розбиття.

Інтегральна сума визначає наближене значення шуканої величини F в області D, . Точність обчислень збільшується при збільшенні подрібнення областіD.

Рис. 1.5

Наприклад. Розглянемо замкнену обмежену область D, яка є квадровною (рис. 1.5). За допомогою прямих паралельних до координатних осей тарозіб’ємо областьD на частини. Площа області D дорівнює сумі площ частин розбиття. Але обчислити площі елементарних частин розбиття, межі яких є кривими лініями досить важко (рис.1.4).

Легко обчислюються площі прямокутників, довжини сторін яких дорівнюють ,(рис.1.5);

; ;;

Площа одного такого прямокутника дорівнює .

Сформуємо інтегральну суму при такому способі розбиття області D.

1. Розглянемо всі прямокутники, які повністю лежать в середині області D (рис.1.6).

Рис. 1.6

При таплощі цих прямокутників стають нескінченно малими величинами,, оскільки розмір їх сторін прямує до нуля,,.

Сума площ вписаних прямокутників наближається до площі області D:

при цьому, різниця між точним і наближенимзначеннями площі стає нескінченно малою величиною, при та Зауваження. Аналогічним чином можна розглядати площі всіх прямокутників, які повністю або частково містять точки області D.

Рис. 1.7

Будемо розглядати прямокутники, які повністю або частково перекривають область D (рис.1.7). При збільшенні подрібнення розбиття сума площ таких прямокутників буде теж наближатись до площі області D.

2. Будемо вважати, що в межах елементарного нескінченно малого прямокутника значення функції є “ практично “ сталим і дорівнює значенню функції у одній з його вершин, наприклад.

3. Знайдемо наближене значення шуканої величини в частині розбиття. Воно дорівнює добутку.

4. Складемо інтегральну суму функції в областіD. Розглянемо суму

наближених значень шуканої величини в частинах розбиття, :

(1.3)

Така сума називається подвійною інтегральною сумою функції в областіD.

Подвійна інтегральна сума визначає наближене значення шуканої величини F в області D, .