ТУ

Федеральное агентство по образованию

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Динамика и прочность машин»

КУРСОВАЯ РАБОТА

ПО ТЕОРИИ УПРУГОСТИ

Выполнила ст. гр. ДПМ-03 Ивукова Л.А.

Проверила Лежнёва А.А.

Пермь, 2006

Задача

Определить напряженно-деформированное состояние двухслойного цилиндра, находящегося в поле температур. Считать известными температуру внешней границы цилиндра и температуру на оси цилиндра. Принять: Т₁=400^о, Т₂=50^о, R₂/R₁=3.0, Е₁⁴⁰⁰=5*10⁴ МПа, α₁⁴⁰⁰=2,1*10^-5. Материал наружного цилиндра – медь. Построить эпюры напряжений.

Распределение температуры в составном цилиндре

Возьмем установившееся распределение температуры. В таком случае функция Т должна удовлетворять уравнению

В полярных координатах это уравнение запишется следующим образом:

откуда

Подставляя граничные условия, находим распределение температуры по первому и второму цилиндрам:

Для первого цилиндра температура Т постоянна и не зависит от радиуса цилиндра Т_I=400.

Для второго цилиндра закон изменения температуры имеет вид:

Решение методами теории упругости

Предположим, что осевое перемещение w всюду равно нулю.

В случае плоской деформации мы имеем три компоненты напряжений σ_r, σ_θ, σ_z; все три деформации сдвига и касательные напряжения равны нулю в силу симметрии относительно оси и постоянства условий в осевом направлении. Соотношения между напряжениями и деформациями имеют вид:

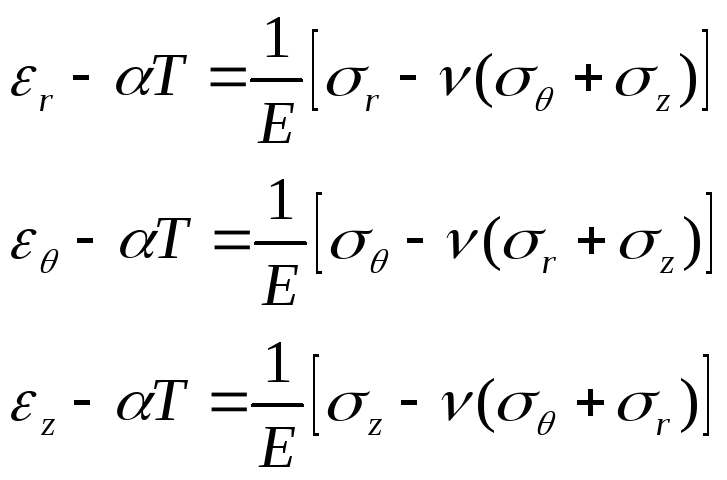
Так как w=0, имеем ε_z=0 и третье из уравнений дает

()

Подставляем это значение в первые два уравнения и получаем

(1)

(2)

Справедливо уравнение равновесия:

Разрешая соотношения (1) и (2) относительно σ_r и σ_θ, получим:

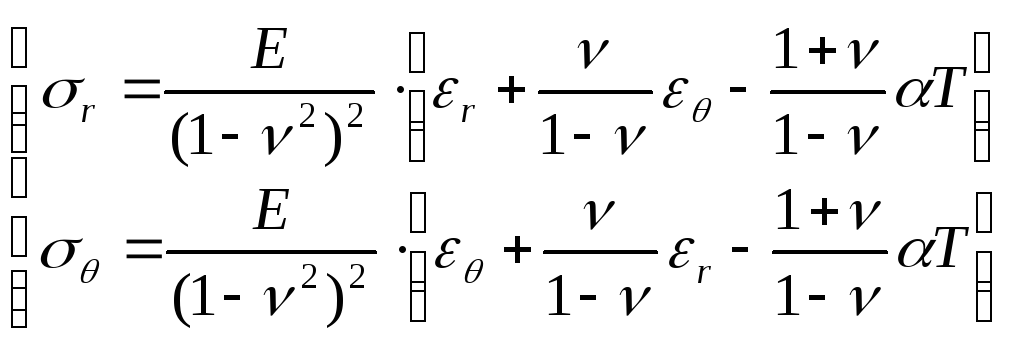
С учетом этого уравнение равновесия принимает вид:

(3)

Если через U обозначить радиальное перемещение, то имеем

Подставляя эти выражения в уравнение (3), получаем

Это уравнение можно перезаписать в виде

Интегрирование уравнения дает:

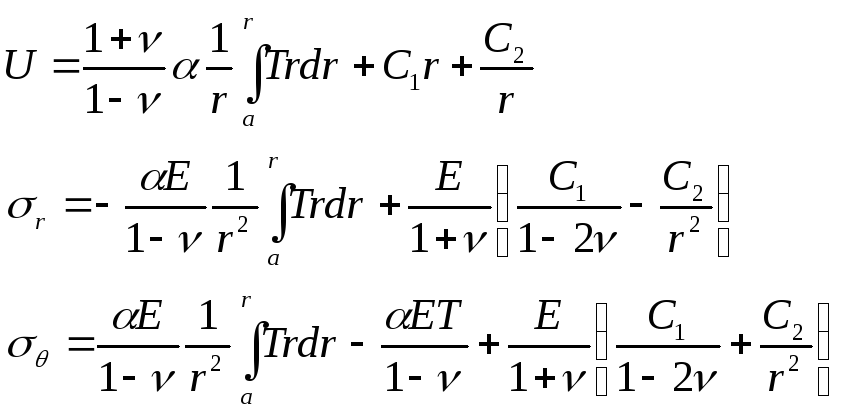
Из уравнения () находим:

(7)

Чтобы всюду выполнялось условие w=0, к концам цилиндра нужно приложить нормальные усилия, распределенные в соответствии с формулой (7). Но теперь следует наложить постоянное осевое напряжение σ_z=С₃, выбрав С₃ таким образом, чтобы результирующее усилие по торцам цилиндра равнялось нулю. Согласно принципу Сен-Венана, самоуравновешенные распределения усилий, остающиеся при этом на обоих концах, будут вызывать среди них только местные эффекты. Напряжения σ_r и σ_θ будут по-прежнему определяться формулами (5) и (6). На перемещение U влияет, однако, осевое напряжение С₃. Поэтому к правой части уравнения (4) должен быть добавлен член . Такое осевое перемещение будет соответствовать однородному распределению напряжения С₃.

Для внутреннего цилиндра:

Принимаем равным нулю нижний предел а в интегралах, входящих в уравнения (4), (5) и (6). Перемещение U должно обращаться в нуль, когда r=0. Поэтому отбрасываем член, содержащий С₂.

Постоянную С₁ находим из условия :

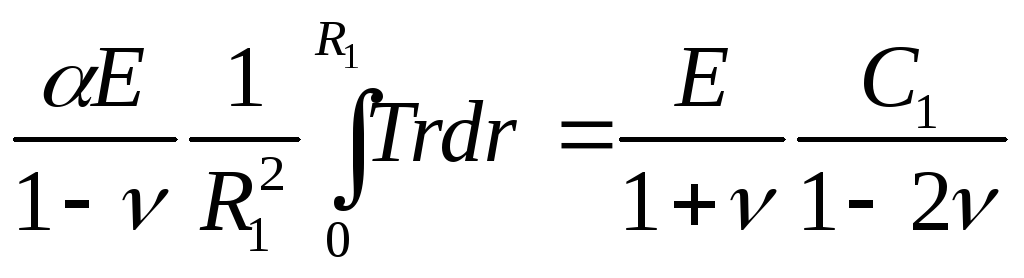(8)

Результирующая осевого напряжения составляет

,

а результирующая постоянного осевого напряжения С₃ равна . Значение С₃, которое обращает в нуль полную осевую силу, определяется отсюда формулой

(9)

При равной нулю осевой деформации (ε_z=0) окончательные выражения для U, σ_r, σ_θ, σ_z;согласно уравнениям (4), (5), (6), (7), (8) и (9) имеют вид:

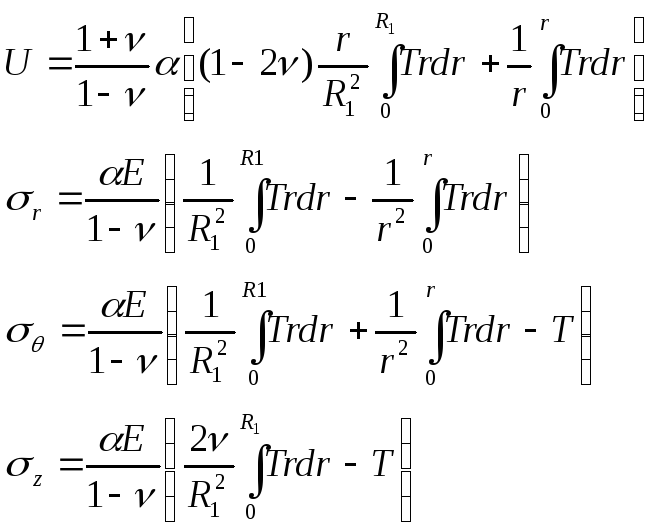
При равном нулю осевом усилии ()напряжения σ_r и σ_θ определяются формулами (11) и (12), а для U и σ_z имеем:

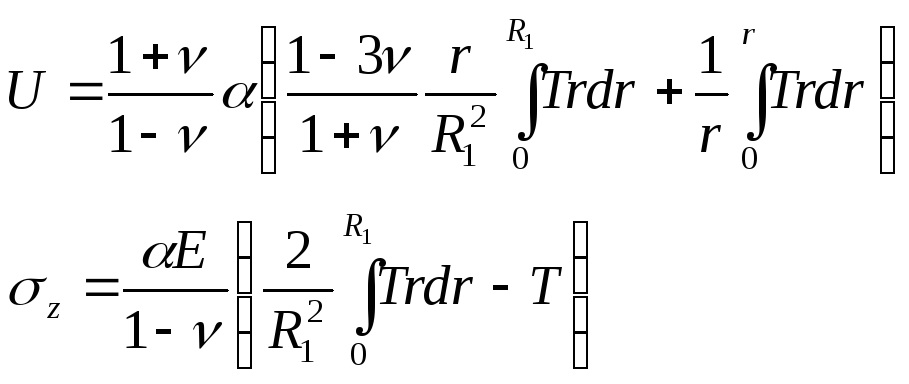
Подставим закон распределения температуры по стенке внутреннего цилиндра в формулы (11), (12), (14) и (15). Получаем:

Для наружного цилиндра:

Постоянные в формулах (4), (5) и (6) следует определить таким образом, чтобы напряжение σ_z при этих двух значениях радиусов было равно нулю. Отсюда

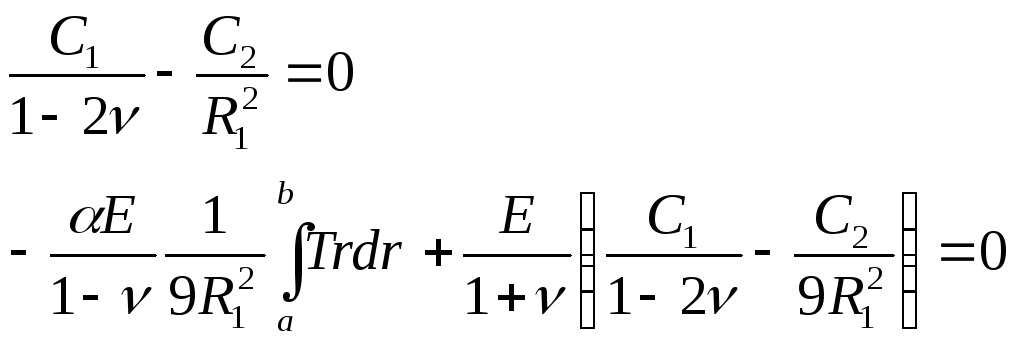
Из этих соотношений следует

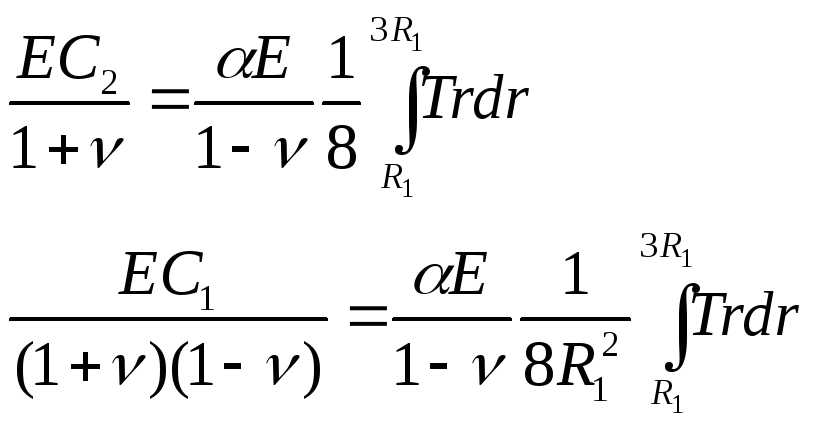
Подставляем эти значения в (5), (6), (7), добавляем к последнему выражению осевое напряжение С₃, требуемое для того, чтобы обратить в нуль результирующую осевую силу, получаем формулы:

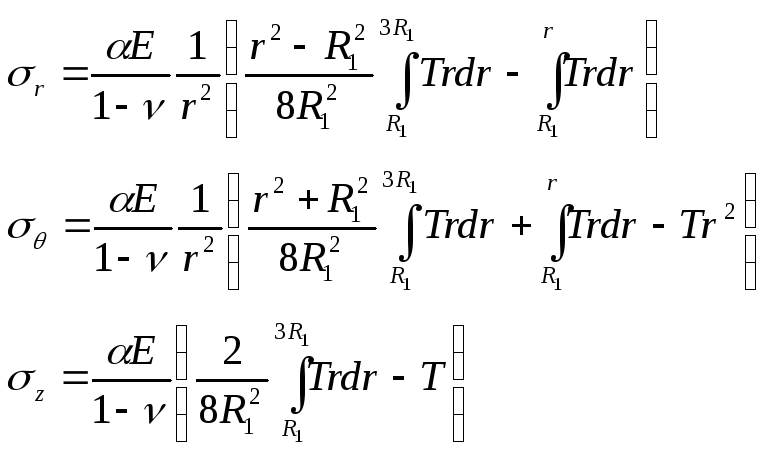
Подставляем закон распределения температуры для наружного цилиндра в эти формулы, получаем следующие выражения для температурных напряжений:

Так как температура Т положительна, то радиальное напряжение во всех точках является сжимающим, и обращается в нуль на внешней и внутренней поверхностях цилиндра.

Компоненты напряжения σ_θ и σ_z достигают максимального и минимального абсолютных значений на внутренней и внешней поверхностях цилиндра.

При r=R₁

При r=R₂

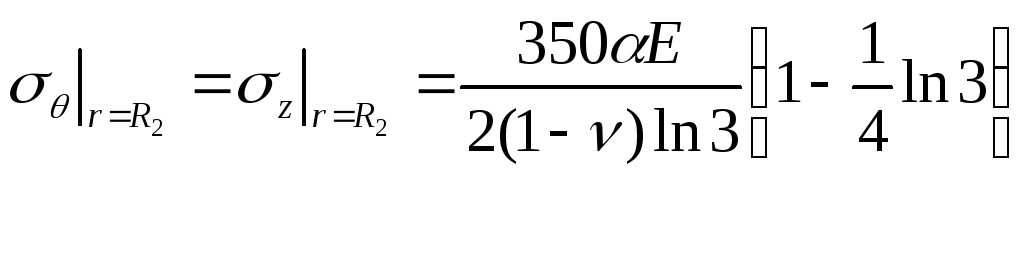
Решение методами сопротивления материалов

Если толстостенный цилиндр нагревается неравномерно, то в нем появляются температурные напряжения, которые суммируются с напряжениями, вызванными давлением.

Часто температурное поле симметрично относительно оси цилиндра и постоянно по его длине. При этом условии также можно считать, что поперечные сечения, лежащие на достаточном расстоянии от концов цилиндра, остаются плоскими и деформация ε_z постоянна.

Обозначим через Т повышение температуры, зависящее от радиуса r, а через α – температурный коэффициент линейного расширения.

Воспользуемся обобщенным законом Гука, добавив к деформациям, обусловленным напряжениями, температурные расширения. Тогда получим следующие формулы:

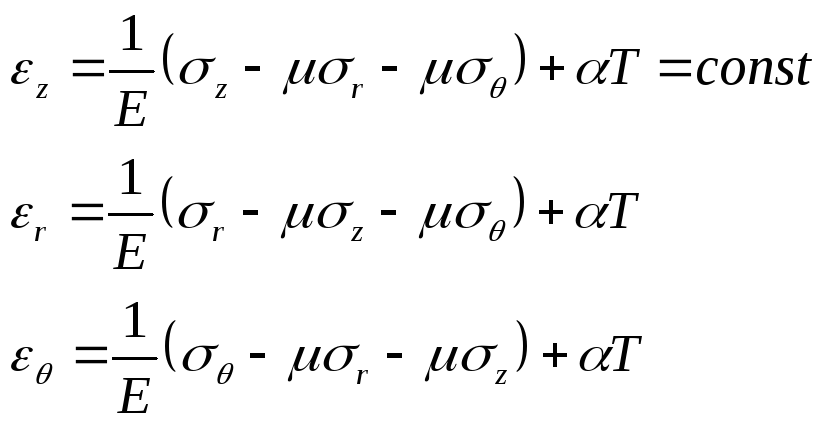(19)

Решая эти уравнения относительно напряжений, найдем, что

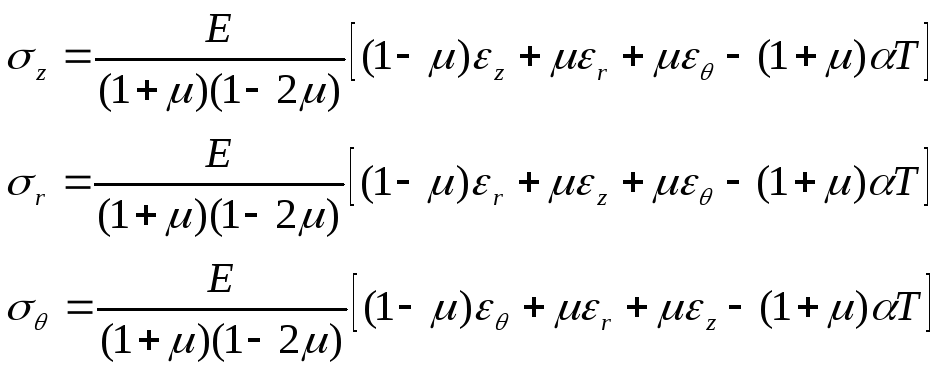(20)

Выражая в этих формулах деформации через перемещения:

и затем подставляя полученные значения через σ_θ и σ_r в уравнение равновесия

получим следующее дифференциальное уравнение для перемещения U

(21)

Это уравнение можно представить в виде:

Интегрируя это уравнение два раза по r, находим общее решение:

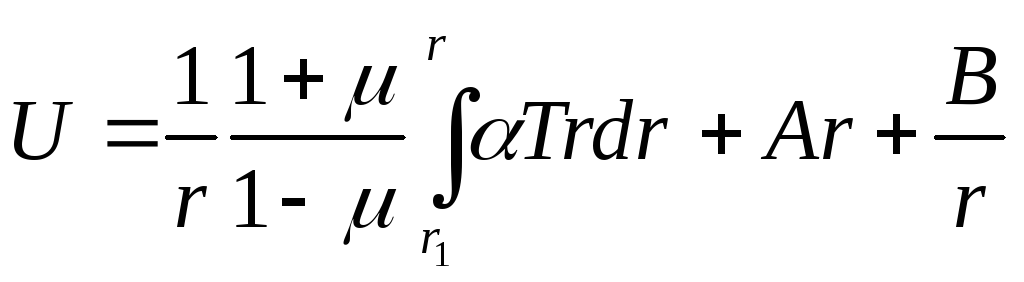(22)

Постоянные А и В определяются из условий для σ_r на внутренней и наружной поверхностях цилиндров:

Внутренний цилиндр:

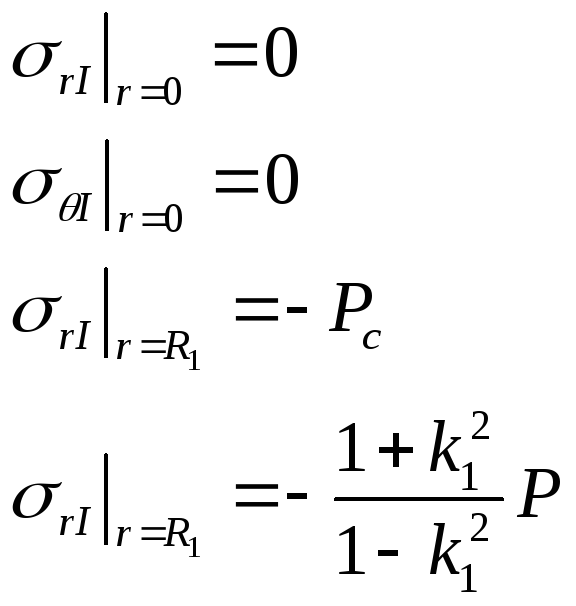
Наружный цилиндр:

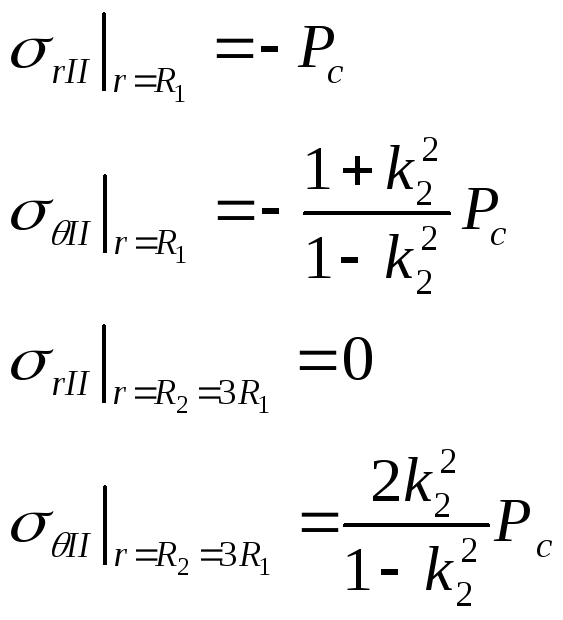
Имеем

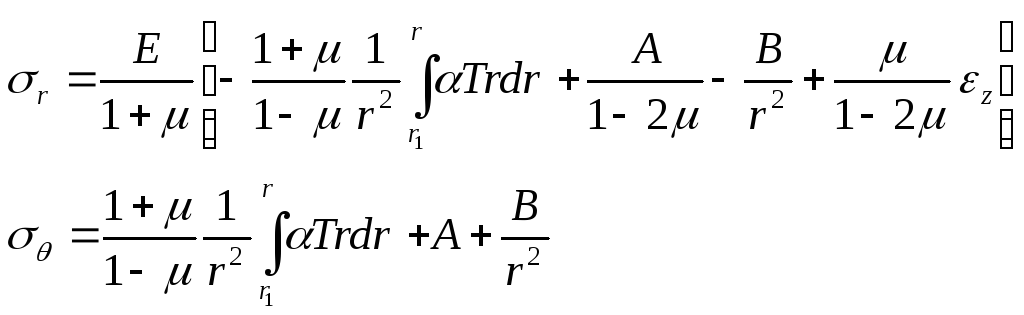(23)

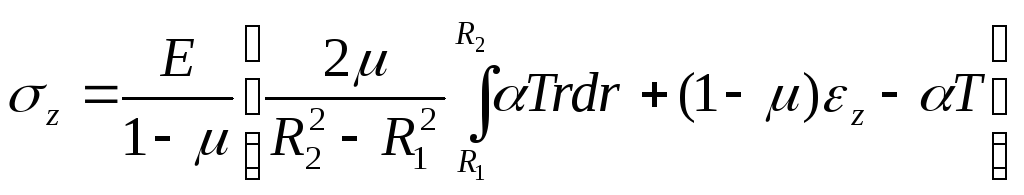(25)

Если цилиндр имеет возможность свободно расширяться, то ε_z можно найти из условия, что продольная сила в поперечном сечении равняется нулю, т.е.

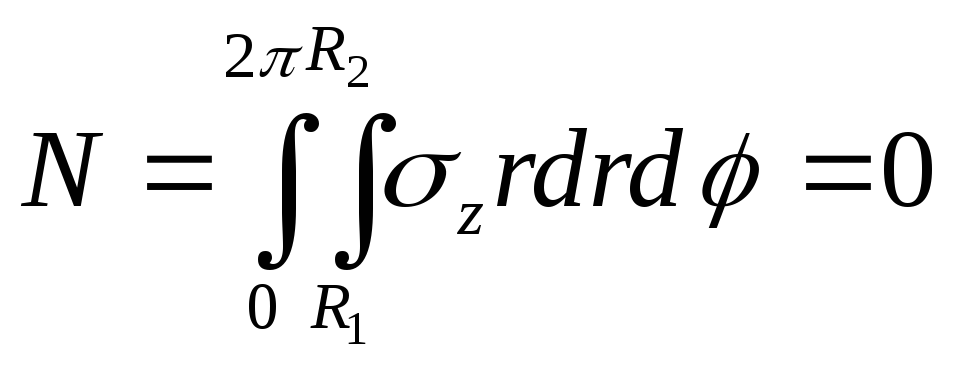
или

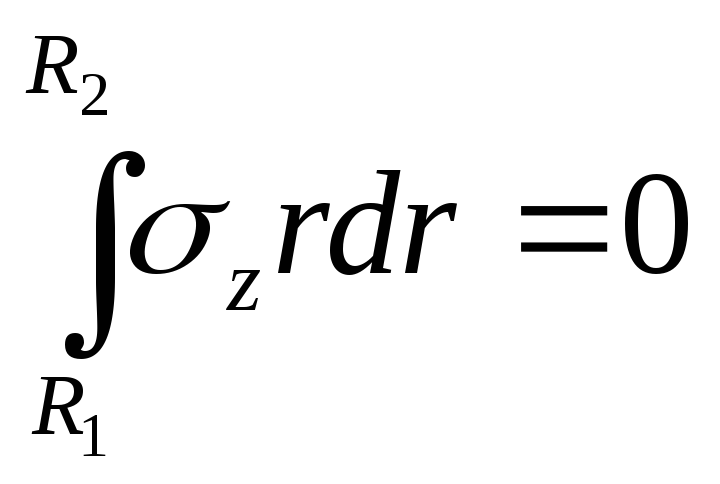
Подставляя сюда значение σ_z из выражения (25), найдем

Окончательное выражение для σ_z следующее:

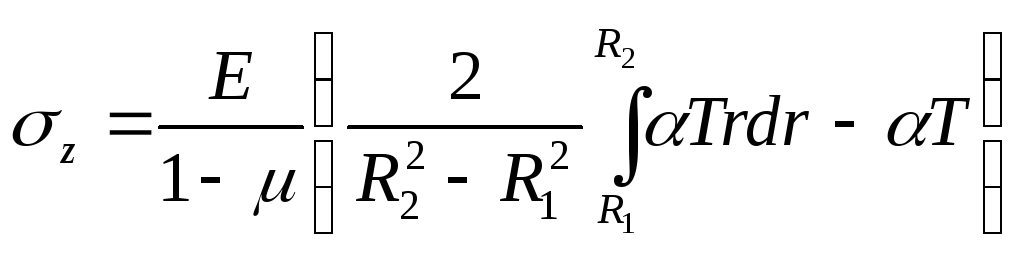(26)

Найдем зависимость давления Р_с по контактной поверхности от величины имевшейся до посадки разности δ между наружным диаметром внутреннего цилиндра I и внутренним диаметром наружного цилиндра II. Эта разность представляет собой величину натяга.

Поскольку после посадки одного цилиндра на другой наружный радиус внутреннего цилиндра и внутренний радиус наружного становятся одинаковыми, то очевидно, что сумма абсолютных величин радиальных перемещений обоих цилиндров на радиусе поверхности контакта, вызванных контактным давлением, должна быть равна половине натяга, т.е.

(27)

Так как величина натяга δ по сравнению с размерами радиуса поверхности контакта, то при вычислении перемещений будем считать, что r_I=r_1II=r_c.

Обозначим через отношение внутреннего радиуса наружного цилиндра к радиусу поверхности контакта, а через отношение радиуса поверхности контакта к радиусу внутреннего цилиндра.

Контактное давление P_c будет наружным для внутреннего цилиндра и внутренним для наружного цилиндра. Абсолютную величину радиального перемещения внутреннего цилиндра на контактной поверхности найдем по формуле:

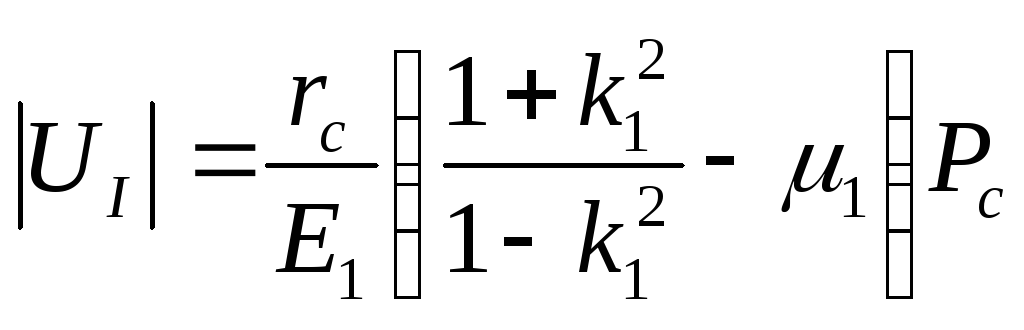, (28)

а наружного – по формуле

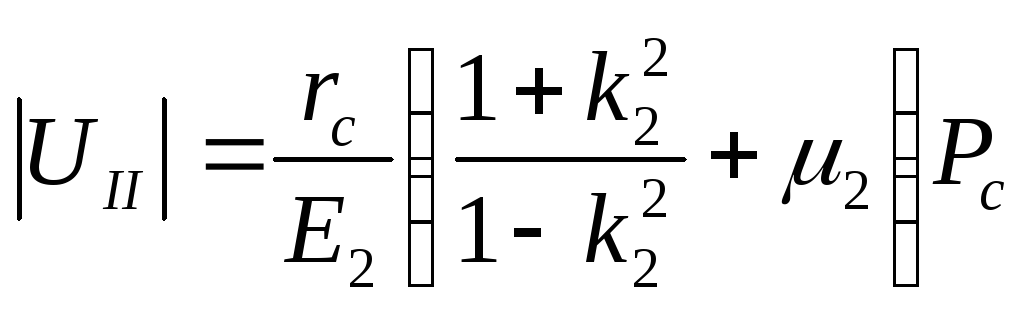. (29)

Подставляя значение этих перемещений в уравнение (27), будем иметь:

.

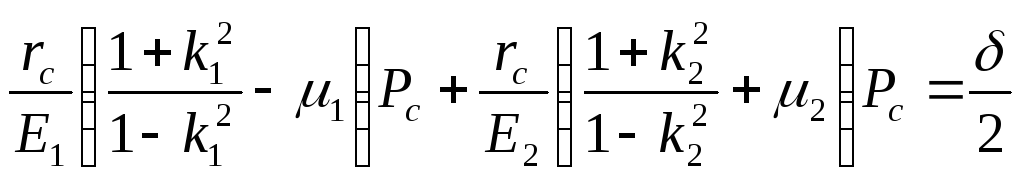Решая уравнение относительно P_c, получаем

. (30)

Напряжения, вызванные давлением P_c, определяются по формулам (23), (24), (25).

Выводы

Список литературы

1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности: Учеб. для строит. спец. вузов. – М.: Высш. шк., 1990.

2. Сопротивление материалов/ Под ред. акад. АН УССР Писаренко Г.С. – 5-е изд. перераб. и доп. – Киев: Вища шк. Головное изд-во, 1986.

3. Тимошенко С.П. Курс теории упругости/Под ред. Григолюка Э.И. – Киев: Наукова думка, 1972.

4. Тимошенко С.П., Гудьер Дж. Теория упругости. перев. с англ. – Главная редакция физико-математической литературы изд-ва «Наука», 1975

Содержание

1. Задача 2

2. Распределение температуры в составном цилиндре 3

3. Решение методами теории упругости 4

4. Решение методами сопротивления материалов 10

5. Выводы 14

6. Список литературы 15

16