1-задание

1. Исследование напряженного состояния

В опасной точке упруго деформированной конструкции выделен бесконечно малый элемент, по граням которого действуют нормальные и касательные напряжения.

1. материал – сталь [σ] = 160 МПа;

2. материал – чугун;

Вычислить:

1. величины главных напряжений и их направление аналитически и при помощи диаграммы Мора;

2. максимальные касательные напряжения и положение площадок, по которым они действуют;

3. определить деформацию по трем главным направлениям и объемную деформацию элемента;

4. проверить прочность конструкции по второй, третьей и пятой теориям и оценить результаты; вычислить эквивалентные напряжения;

5. показать площадки разрушения;

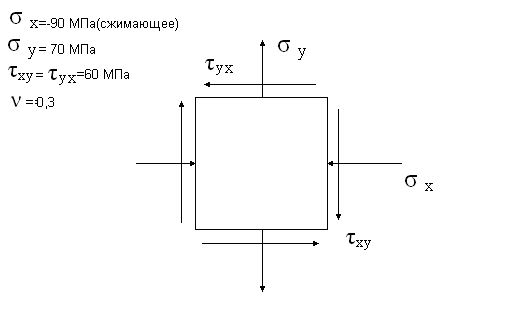
1. Вычисление величин главных напряжений и их направление аналитически и при помощи диаграммы Мора

а) аналитическим способом:

Вычислим величины главных напряжений по формуле:

σ _{max(min) =} <1.1>

Главные напряжения – это напряжения возникающие на главных площадках, т.е площадках на которых отсутствуют касательные напряжения.

Подставляя известные значения σ_x , σ_y и τ_xy в формулу <1.1> найдём σ _max(min):

σ _{max(min) =}

Тогда σ _max = -10+100 = 90 МПа;

σ _min = -10-100 = -110 МПа;

так как σ ₁ > σ ₂ > σ ₃ , следовательно, σ ₁ = 90 МПа;

σ ₂ = 0 МПа;

σ ₃ = -110 МПа;

Определим угол, между главными площадками и осью σ:

<1.2>

Подставляя известные значения σ_x , σ_y и τ_xy в формулу <1.2> найдём α₀:

б) при помощи диаграммы Мора (рис.1.1):

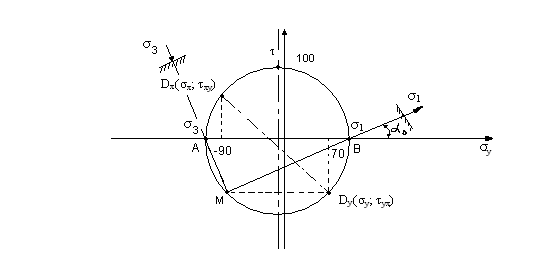
(рис.1.1)

Угол откладывается от большего напряжения (>)

( , так как отрицат.; , так как положит.)

2. Вычисление максимальных касательных напряжении и положение площадок, по которым они действуют

Вычисляем величину максимальных касательных напряжении по формуле:

τ_max = <1.3>

Максимальные касательные напряжения – это касательные напряжения, возникающие по касательной к главным площадкам.

Подставляя известные значения σ₁ и σ₂ в формулу <1.3> найдём τ_max:

τ_max =

Положение площадок и максимальных касательных напряжении (τ_max), указаны на рисунке 1.2

(рис. 1. 2)

3. Определение деформации по трем главным направлениям и объемной деформации элемента:

По принципу независимости действия сил: от действия одного σ₁ в направлении 1 деформация равна ε₁₁ = ; в направлении 2 : ε₁₂ = -ν; в направлении 3 : ε₁₃ = - ν;

Аналогично при действии σ₂ и σ₃. Суммируя деформации, получаем:

ε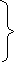₁ =

ε₂ = <1.4>

ε₃ =

Здесь Ε – модуль упругости (для стали: Ε = 2 · 10⁵ МПа); ν – коэффициент Пуассона (ν = 0,28). Уравнения <1.4> представляют собой обобщённый закон Гука для объёмного напряжённого состояния. Деформации ε_1, ε₂ и ε₃ в направлении главных напряжений называются главными деформациями.

Зная ε_1, ε₂ и ε_{3 ,} можно вычислить изменение объёма при деформации. Возьмём кубик 1 · 1 · 1 см. Объём его до деформации V₀ = 1 см³. Объём после деформации V = (1 + ε₁) (1 + ε₂) (1 + ε₃) ≈ 1+ ε₁ + ε₂+ ε₃ (произведениями ε, как величинами, малыми по сравнению с самими ε, пренебрегаем).

Тогда объёмна деформация элемента будет равна:

ε _v = <1.5>

Решая уравнения <1.4> и <1.5>, найдем деформации по трем главным направлениям и объемную деформацию элемента

ε₁ =

ε₂ =

ε₃ =

ε _v =

4. Проверить прочность конструкции по второй, третьей и пятой теориям и оценить результаты; вычислить эквивалентные напряжения:

Теория прочности – это гипотеза о причине разрушения, позволяющая оценить прочность при сложном напряжённом состоянии, если известна прочность при простом растяжении-сжатии σ_экв ≤ [σ].

1. 2-я теория – теория наибольших линейных деформаций (для хрупкого материала): Разрушение сложного напряжённого состояния наступит тогда, когда наибольшая линейная деформация достигнет той величины, при которой наступает разрушение, в случае простого разрушения-сжатия.

ε₁ =

σ_экв2 = <1.6>

Решая уравнение <1.6> находим σ_экв

σ_экв2 =

2. 3-я теория – теория наибольших касательных напряжений (для пластичных материалов):

Текучесть материала наступит тогда, когда наибольшая линейная деформация достигнет той величины, при которой наступает разрушение, в случае простого разрушения-сжатия.

τ_max = ≤ [τ]

σ_экв3 = <1.7>

Решая уравнение <1.7> находим σ_экв

σ_экв3=

3. 4-я теория – теория Мора (для хрупких и пластичных материалов):

σ_экв = <1.8>

κ – критерий Баландина П. П. (пластичный – κ = 1; хрупкий – κ = 0,23)

Решая уравнение <1.8> находим σ_экв

Для пластичного материала: σ_экв4 =

Для хрупкого материала: σ_экв4 =

Определим коэффициент запаса прочности по 2-ой и 3-ей теориям:

η = <1.9>

Здесь η - коэффициент запаса прочности; [σ] = допускаемое напряжение для конструкции [σ] = 160МПа.

Решая уравнение <1.9> находим η₂ и η₃:

η₂ =

η₃ =

Вывод: наибольший запас прочности, в нашем случае, имеет хрупкий материал (т.е чугун).

5. Площадки разрушения:

Согласно 3-й теории прочности площадки сдвига нах-ся под углом 45 градусов и