
- •Пермский Государственный Технический Университет
- •Введение
- •1. Теория множеств
- •1.1 Понятие множества
- •1.2.Операции над множествами
- •1.3.Диаграммы Эйлера - Венна
- •1.4. Алгебра множеств
- •1.5. Кортеж. График
- •1.6. Соответствия
- •2 3 4 5
- •1.7. Отношения
- •1.7.1 Отношение эквивалентности
- •1.7.2.Отношения порядка
- •1.7.3. Морфизмы
- •1.8. Решетки
- •1.8.1. Диаграммы Хассе
- •1.8.2. Понятие решетки
- •1.8.3. Алгебраическое представление решеток. Булевы решетки
- •1.8.4. Подрешетки
- •1.9.4.Мощность множества r. Теорема Кантора
- •1.9.5. Арифметика бесконечного
- •2.1.1.Операции над высказываниями
- •2.1.2.Построение и анализ сложных высказываний
- •2.1.3.Алгебра высказываний
- •2.1.4.Формы представления высказываний
- •2.1.5.Преобразование высказываний
- •2.1.6.Минимизация высказываний методом Квайна
- •2.1.7.Минимизация с помощью карт Вейча
- •2.1.8.Функциональная полнота
- •2.2.Логика предикатов
- •2.2.1.Основные равносильности для предикатов
- •2.2.2.Получение дизъюнктов
- •2.3.Аксиоматические теории
- •2.3.1.Аксиоматическая теория исчисления высказываний
- •2.3.2.Непротиворечивость и полнота аксиоматической теории исчисления высказываний
- •2.4.Аксиоматические теории первого порядка
- •2.5.Метод резолюций
- •2.6.Система Генцена
- •2.7.Система Аристотеля
- •2.8. Примеры неклассических логик
- •3. Теория Автоматов
- •3.1.Понятие автомата
- •Законы функционирования автоматов
- •3.2.Примеры автоматов
- •3.3.Минимизация автоматов
- •3.4.Особенности минимизации автомата Мура
- •3.5.Переход от автомата Мура к автомату Мили и наоборот
- •4.Теория графов
- •4.1. Понятие графа
- •4.2.Теорема Эйлера
- •4.3.Полные графы и деревья
- •4.4.Деревья
- •4.5.Алгоритм Краскала
- •4.6.Планарные графы
- •4.7.Задача о 4 красках
- •4.8.Определение путей в графе
- •4.9.Приведение графа к ярусно-параллельной форме
- •4.10.Внутренняя устойчивость графа
- •4.11.Множество внешней устойчивости. Ядро графа
- •4.12.Клика
- •5. Теория групп
- •5.1.Понятие группы
- •5.2.Морфизмы групп
- •5.3.Инвариантные (нормальные) подгруппы
- •5.4.Группа Диэдра (d3)
- •5.5.Смежные классы
- •5.6.Фактор-группы
- •5.7.Группа Клейна четвертой степени
- •6. Теория алгоритмов
- •6.1.Понятие алгоритма
- •6.2.Конкретизация понятия алгоритма
- •6.3.Сложность вычислений
- •6.4.Машины Тьюринга
- •6.5.Нормальные алгорифмы Маркова
- •6.6.Рекурсивные функции
- •6.7.-Исчисление
- •7.Формальные грамматики
- •7.1. Понятие формальной грамматики
- •7.2.Деревья вывода
- •7.3.Классификация языков по Хомскому
- •7.4.Распознающие автоматы
- •7.5.Понятие транслятора
- •7.6.Основные функции компилятора. Лексический анализ
- •7.7.Переход от недетерминированного распознающего автомата к детерминированному
- •7.8.Переход от праволинейной грамматики к автоматной
- •7.9.Lex
- •7.10.Детерминированные автоматы с магазинной памятью (мп-автоматы)
- •7.11.Транслирующие грамматики
- •7.12. Sи q - грамматики
- •7.13.Ll(1) - грамматики. (left - leftmost)
- •7.14.Метод рекурсивного спуска
- •7.15.Lr - грамматики (left - rightmost)
- •7.16.Функции предшествования
- •7.17.Атрибутные грамматики
- •7.18.Yacc
- •7.19.Область действия и передача параметров
- •7.20.Генерация выходного текста. Польская инверсная запись
- •7.21.Оптимизация программ
- •8. Функциональное программирование
- •9. Логическое программирование. Язык Пролог
- •10. Объектно-ориентированное программирование
- •Заключение
- •Литература
3. Теория Автоматов
3.1.Понятие автомата
Автомат - дискретный преобразователь информации, на вход которого поступают входные последовательности сигналов (входные слова). Он формирует выходные последовательности сигналов на основании своих внутренних состояний и входной последовательности сигналов.
В курсе рассматривается абстрактная теория автоматов.
Нас будет интересовать их поведенческий аспект. Автомат для нас – математическая модель, а не физическое устройство. Автоматы фактически позволяют реализовать логику, зависящую от времени.
Не рассматриваемая здесь структурная теория автоматовзанимается реализаций абстрактного автомата с помощью физических сущностей, вроде элементов памяти (например, триггеров) и комбинационных (логических) схем…
Будем иметь в виду две ключевые абстракции:
1. Автомат функционирует в абстрактном времени.
2. Все переходы происходят мгновенно.
Автомат есть система шести объектов:
= <X, Y, Q, f, , q0>
X = {x1,...,xn} - конечный входной алфавит (множество входных сигналов).
Y = {y1,...,ym} - конечный выходной алфавит (множество выходных сигналов).
Q = {q0, q1,...,qk} – множество состояния автомата.
Если множество конечно автомат называется конечным.
f (q, x) - функция переходов.
(q, x) - функция выходов.
q0Q - начальное состояние.
Законы функционирования автоматов
}
q
Автомат
I-го рода (автомат Мили)
y(t) = (q(t-1), x(t))
}
q
Автомат
II-го рода
y(t) = (q(t), x(t))
} Правильный
автомат II-го рода (автомат Мура)
q(t) = f(q(t-1), x(t))
y(t) = (q(t))
3.2.Примеры автоматов
Замечание. Для удобства восприятия и сокращения описания будем говорить об автоматах как об автоматических роботоподобных устройствах, хотя на самом деле это, как уже было сказано, лишь математические модели, преобразующие входные слова в выходные и не имеющие дела с физическими сущностями, вроде монет, билетов и т.п.
Пример 1(автомат Мили):
Построить (синтезировать) автомат, на вход которого могут поступать в любой последовательности и, возможно, с повторениями монеты (как в добрые старые времена) 1; 2 и 3 копейки. Автомат продает билет, если сумма опущенных монет равна 3. В случае превышения суммы автомат возвращает деньги.
Входной алфавит в описании задан явно: Х = {1, 2, 3}.
Выходной алфавит будет содержать буквы (сигналы): Б – выдает билет, В – возвращает деньги, Н – ничего не выдает (это такой специфический выходной сигнал). То есть У = {Б, В, Н}.
Можно представить автомат в виде графа, где вершины представляют состояния, а к каждой стрелке приписана пара входной сигнал/выходной сигнал. То есть размеченные стрелки отражают функции переходов и выходов.

3/В 1/Н 1/Н
2/Б 1/Н
2/Н
3/Б 1/Б 2/Н
2/В 3/Б
От представления автомата в виде графа можно очевидным образом перейти к его табличному представлению, которое также однозначно определяет автомат. Табличное представление предпочтительно для автоматов с большим числом состояний и при представлении автоматов в компьютере.
Можно построить для данного автомата таблицы
переходов
|
Т.П. |
q0 |
q1 |
q2 |
q3 |
|
f |
q1 |
q2 |
q3 |
q1 |
|
2 |
q2 |
q3 |
q0 |
q2 |
|
3 |
q3 |
q0 |
q0 |
q3 |
и
выходов
|
Т.В. |
q0 |
q1 |
q2 |
q3 |
|
|
Н |
Н |
Б |
Н |
|
2 |
Н |
Б |
В |
Н |
|
3 |
Б |
В |
В |
Б |
Пример 2(автомат Мура).
Построить автомат, на вход которого могут поступать монеты 1, 2, 3 коп. Автомат выдает сигнал “чет”, если поступившая сумма в данный момент четная и “нечет”, если наоборот.
2 1,3




1,3 2 Ч Н



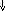








 чет нечет
чет нечет
Это автомат Мура. Поэтому выходные сигналы приписаны не стрелкам, а к состояниям, которыми они однозначно определяются. Табличное представление сводится к одной таблице – расширенной таблице переходов. В ней добавляется верхняя строка, позволяющая приписать выходные сигналы состояниям.
|
-
выходные сигналы - состояния
|
Чет |
Нечет |
|
|
Ч |
Н |
|
1 |
Н |
Ч |
|
2 |
Ч |
Н |
|
3 |
Н |
Ч |
