
- •Министерство образования и науки рф
- •Алгоритм экспертных процедур
- •Метод Дельфи и его модификации
- •Методы ранжирования альтернатив
- •Полученная таким образом матрица
- •Метод минимального расстояния
- •Объекты и средства исследования
- •Подготовка и порядок работы
- •Результаты работы
- •Варианты заданий
- •Библиографический список
Метод минимального расстояния
Изложенные выше методы обработки результатов опроса экспертов сводятся к определения средних значений оценок. Может быть предложен и другой подход для определения суммарной оценки. Рассмотрим геометрическое представлениеранжировочных оценок, даваемых экспертами. Предположим, что для каждой из П альтернатив выделена числовая ось гиперпространства. Тогда ранжировка альтернатив в этом гиперпространстве может быть представлена некоторой точкой. Координаты этой точки, изображающей систему предпочтений эксперта, определяются рангами, отложенными по соответствующим числовым осям. Система предпочтений каждого эксперта для данной совокупности альтернатив будет изображаться точкой в таком гиперпространстве. Разумно предположить, что в качестве суммарной оценки может быть выбрана такая, изображающая точка которой находится ближе всего ко всем точкам гиперпространства, изображающим предпочтения всех экспертов. Таким образом, если ввести понятие расстояния между экспертными оценками, то в качестве суммарной оценки можно определить такую, сумма расстояний до которой от оценок всех экспертов будет минимальной, т.е.
![]()
![]() - искомая оценка - ранжировка, выступающая
в качестве аргумента, минимизирующего
сумму расстояний
- искомая оценка - ранжировка, выступающая
в качестве аргумента, минимизирующего
сумму расстояний![]() ;
;![]() - расстояние между ранжировками;
- расстояние между ранжировками;![]() -
ранжировкак-го
эксперта;
-
ранжировкак-го
эксперта;
![]() -
множество всех возможных нестрогих
ранжировок, задаваемых матрицами
-
множество всех возможных нестрогих
ранжировок, задаваемых матрицами![]() в которых
в которых![]() только тогда, когда
только тогда, когда![]() ,
,![]() = -1, когда
= -1, когда![]() ;
;![]() = 0, когда
= 0, когда![]() и I=[1,n].
и I=[1,n].
Расстояние между ранжировками наиболее часто определяется
следующим способом.
![]()
![]() и
и![]() две ранжировки, то
две ранжировки, то
Такое понятие расстояния между ранжировками удовлетворяет следующим условиям:
в
случае, если ранжировки совпадают (А=В,
т.е.
![]() );
);
расстояние
между двумя ранжировками всегда
неотрицательно
![]()
расстояние
не зависит от направления измерения
![]() =
=![]() ;
;
минимальное положительное расстояние между двумя ранжировками равно единице (для выполнения этого условия в понятие расстояния введен нормирующий множитель 1/2);
расстояние
![]() не зависит от того, как пронумерованы
альтернативы, т.е. расстояние
не зависит от того, как пронумерованы
альтернативы, т.е. расстояние![]() инвариантно относительно одинаковых
перестановок альтернатив внутри
ранжировок;
инвариантно относительно одинаковых
перестановок альтернатив внутри
ранжировок;
![]()
причем
равенство справедливо только тогда,
когда ранжировка с находится между В
и А, т.е. когда
![]() или
или![]() для всехi
и j
.
для всехi
и j
.
Ранжировка, сумма расстояний до которой от всех ранжировок экспертов минимальна, называется медианой Кемени - Онелла.
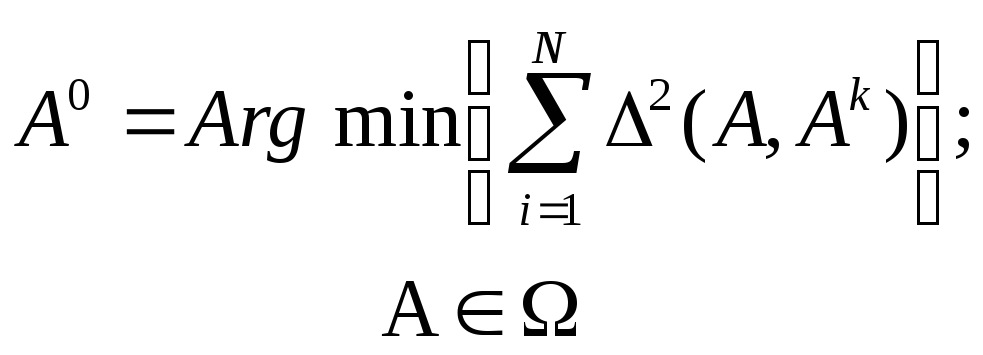
Для более наглядного представления о методе минимального расстояния рассмотрим некоторый гипотетический пример.

что равносильно следующей системе предпочтений экспертов:
![]() ,
,
![]() ,
,![]()
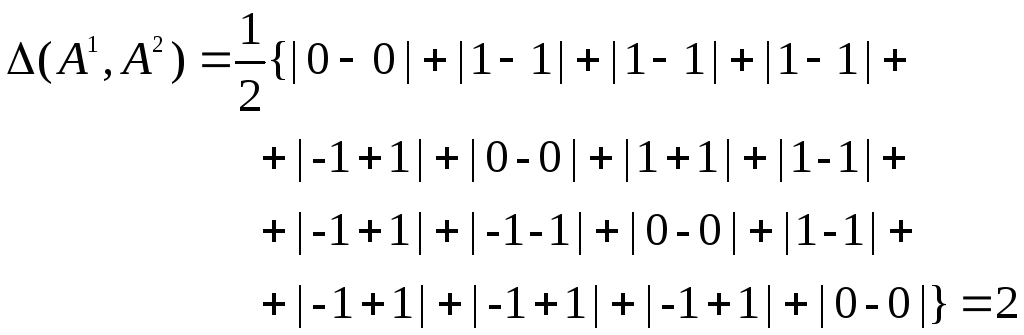
![]()
![]()
Если в качестве суммарной оценки взять А1, то
![]()
При А2 получим
![]()
при А3 получим
![]()
В принципе нужно рассмотреть все. возможные ранжировки для нахождения действительной медианы Кемени - Скелла. Например,
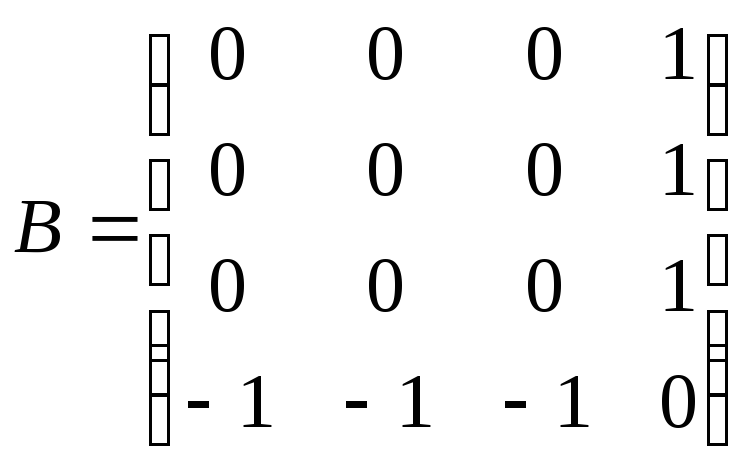
![]()
![]()
![]()
