выч методы не разобраны! / 2-лаба / Расчётная работа №2 / Вариант 37 / Задание 7.doc
Задание №7:
Решить интегральное уравнение, используя заданную формулу (при заданном «n»). Оценить погрешность.
Методом Симпсона,
Решение:
-
ядро
интегрального уравнения.
- свободный член
(известная функция от
).
Пределы интегрирования:
.
Шаг
,
т.е.
По методу Симпсона
-
узлы, в которых можно найти значение
искомой функции.
В соответствии с
методом обозначим
,
где
Система уравнений:
,
у нас
,
,
Пусть
,
.
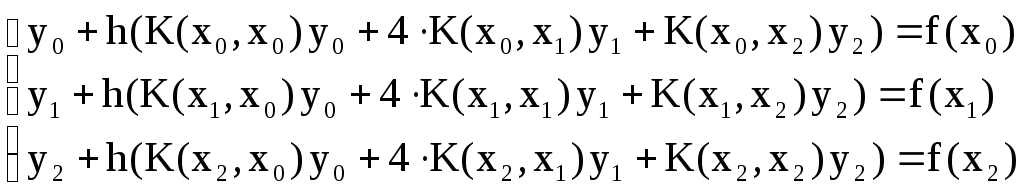
Найдём
и
:
После преобразований:
Решения этой системы:
Итак,
определена неизвестная функция
на дискретном множестве точек.
Погрешность метода Симпсона можно оценить по формуле:
Ответ:
,
,
