3_теориЛеготкина / выч методы / отчет по 1 лабе_КРЭС-05

Пермский Государственный Технический Университет

Электротехнический факультет

Кафедра автоматики и телемеханики

Вычислительные методы.

Отчет по лабораторной работе №1.

Интерполирование функций.

Выполнили: студент гр. КРЭС-05

Пьянков А.Л.

Проверила: Леготкина Т.С.

Пермь 2007 г.

Цель работы:

1. Научиться применять численные методы интерполяции функций, заданных таблично.

2. Изучить метод интерполирования функций с помощью кубических сплайн – функций.

Задано:

Задано множество вещественных абсцисс Х0, Х1, …, Хn и соответствующие координаты Y0, Y1, …, Yn. Здесь Х0< Х1< …< Хn, а каждое Yi – некоторое вещественное число, отвечающее Xi, определенное математически или являющееся результатом какого – либо наблюдения.

Задача одномерной интерполяции состоит в построении функции f(x), такой, что f(x_i)=y_i для всех i, т.е. нужно найти многочлен P_n(x) степени не выше n, значения которого в точках X_i (i=0,n) совпадают со значениями данной функции, т.е. P_n(x_i)=y_i. Многочлен P_n(x) является интерполяционным многочленом (полиномом), а точки x_i являются узлами интерполяции.

Задана таблица:

	0	1	2	3	4	5	6	7	8
xi	-4	-3	-2	-1	0	1	2	3	4
yi	0	0	-2	1	0	-1	2	0	0

Необходимо составить интерполяционный полином Лагранжа и Кубическую сплайн-функцию для нахождения аналитического выражения функции f(x), при этом на экран должны выводиться графики полинома Лагранжа и кубической сплайн - функции.

Интерполяционная формула Лагранжа.

Пусть x_i (i=0,n) произвольные узлы, а y_i=f(x_i) – значение функции в узлах. Многочленом степени n, принимающем в точке x_i значения y_i, является интерполяционный многочлен Лагранжа

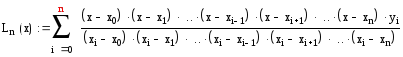
Сплайны:

Сплайном называется функция, которая вместе с несколькими производными непрерывна на заданном отрезке, а на каждом частичном отрезке является некоторым алгебраическим многочленом. Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на заданном отрезке производной – дефектом сплайна.

На практике наиболее широкое применение получили сплайны третьей степени, имеющие на заданном отрезке непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими.

На участке [x₀, x_n] требуется найти функцию ф(х), удовлетворяющую следующим условиям:

1.Функция ф(х) на участке [x₀, x_n] должна быть непрерывна вместе со своими первой и второй производными.

2. На каждом участке [x_i-1, x_i] функция ф_i(х) должна описываться кубическим полиномом

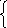a_oi+a_1i(x-x_i-1)+a_2i(x-x_i-1)²+a_3i(x-x_i-1)³ x с[x_i-1, x_i];

ф_i(x)=

0, x ¢[ x_i-1, x_i] i=1,n

Общий сплайн

при х с[x₁, x_n].

3. Значения сплайна в узлах интерполяции равны значениям заданной функции, т.е. ф(х_i)=y_i , i=0,n.

Текст программы на языке Pascal:

uses graph, crt;

const

N =8;

x:array [0..N] of real =(-4, -3, -2, -1, 0, 1, 2, 3, 4);

y:array [0..N] of real =(0, 0, -2, 1 ,0 ,-1 , 2, 0, 0);

var

m, h, g, f:array[0..n] of real;

a, b, c, d:array[1..n] of real;

lk: array[0..N] of real;

w, i, j: word;

kx: real;

ky: real;

xx: real;

xh: real;

xC, yC: word;

procedure InitScreen;

var

gm, gd, errorcode: integer;

begin

gd := VGA; gm := VGAHi;

initgraph( gd, gm, 'c:\bp\bgi');

ClearViewPort;

xC:=Round(getmaxx/2); yC:=Round(getmaxy/2);

kx :=getmaxx/(x[n]-x[0]);

ky :=getmaxx/(x[n]-x[0]);

SetColor(White);

Line(xC, 0, xC, getmaxy);

Line(0, yC, getmaxx, yC);

SetLineStyle(DottedLn, 0, NormWidth);

SetColor(LightGray);

i:=xC;

j:=xC;

while i<=getmaxx do begin

i:=Round(i+kx);

j:=Round(j-kx);

Line(i, 0, i, getmaxy);

Line(j, 0, j, getmaxy);

end;

i:=yC;

j:=yC;

while i+ky<=getmaxy do begin

i:=Round(i+ky);

j:=Round(j-ky);

Line(0, i, getmaxx, i);

Line(0, j, getmaxx, j);

end;

end;

function L(xx: real):real;

var

i, j: word;

sum, Pn1: real;

begin

sum := 0;

for i := 0 to n do begin

Pn1 := 1;

for j := 0 to n do begin

if j <> i then Pn1 := Pn1 * (xx-x[j]);

end;

sum := sum + lk[i]*Pn1;

end;

L:= sum;

end;

function Spline(xx:real): real;

var

i: word;

begin

if (xx < x[0]) or (xx > x[n]) then begin

Spline:=0;

exit;

end;

i := 1;

while xx > x[i] do i:=i+1;

Spline:= a[i]*(x[i]-xx) * (x[i]-xx) * (x[i]-xx) +

b[i]*(xx-x[i-1])*(xx-x[i-1])*(xx-x[i-1]) +

c[i]*(x[i]-xx) + d[i]*(xx-x[i-1]);

end;

procedure PrintSpline;

var

i: word;

begin

WriteLn('Полученные сплайны:');

for i:=1 to n do begin

WriteLn(a[i]:2:2, '*(', x[i]:2:2, ' - x)^3 + ', b[i]:2:2, '*(x - ',

x[i-1]:2:2, ')^3 + ', c[i]:2:2, '*(', x[i]:2:2, ' - x) + ',

d[i]:2:2, '*(x - ', x[i-1]:2:2, ')');

end;

end;

begin

for i := 0 to n do begin

lk[i] := y[i];

for j := 0 to n do begin

if j <> i then lk[i] := lk[i]/(x[i]-x[j]);

end;

end;

for i:=1 to n do

h[i]:= x[i] - x[i-1];

g[1]:= 2*(h[1] + h[2]);

f[1]:= 6*((y[2] - y[1])/h[2] - (y[1] - y[0])/h[1]);

for i:= 2 to n-1 do begin

g[i]:= 2*(h[i] + h[i+1])-sqr(h[i])/g[i-1];

f[i]:= 6*((y[i+1]-y[i])/h[i+1]-(y[i]-y[i-1])/h[i])-f[i-1]*h[i-1]/g[i-1];

end;

m[n-1] := f[n-1]/g[n-1];

for i:=n-2 downto 1 do

m[i] := (f[i] - h[i+1]*m[i+1])/g[i];

for i:=1 to n do begin

a[i] := m[i-1]/(6*h[i]);

b[i] := m[i] / (6*h[i]);

c[i] := (y[i-1] - 1/6 * m[i-1]*sqr(h[i]) ) / h[i];

d[i] := (y[i] - 1/6 * m[i] * sqr(h[i]) ) / h[i];

end;

InitScreen;

xh:=(x[n]-x[0])/getmaxx;

SetLineStyle(SolidLn, 0, NormWidth);

SetColor(blue);

moveto(0, yC);

xx:=x[0];

while xx<=x[n] do begin

lineto(Round(xC+xx*kx), Round(yC-Spline(xx)*ky));

xx:=xx+xh

end;

SetColor(red);

moveto(0, yC);

xx:=x[0];

while xx<=x[n] do begin

lineto(Round(xC+xx*kx), Round(yC-L(xx)*ky));

xx:=xx+xh

end;

SetColor(White);

for i:=0 to n do

Circle(Round(xC+x[i]*kx), Round(yC-y[i]*ky), 3);

readkey;

closegraph;

clrscr;

PrintSpline;

readkey;

clrscr;

end.