Схемотехника(Тюрин) / лекции по схематехнике / пример дз схт

Пример выполнения СРС

Задание №1

Дано: двоичная переключательная функция (ПФ) № 174₁₀

Получим соответствующий двоичный код : 10101110₂ (2⁷ + 2⁵ + 2³ + 2² + 2¹).

Таблица истинности ПФ № 174₁₀ :

переменные			ВС	f(abc)
а	b	с
0	0	0	0	0	20
0	0	1	1	1	21
0	1	0	2	1	22
0	1	1	3	1	23
1	0	0	4	0	24
1	0	1	5	1	25
1	1	0	6	0	26
1	1	1	7	1	27

Получим восьмеричный код ПФ: 256₈

Получим шестнадцатеричный код ПФ : АЕ₁₆

Получим символическую форму:

f(abc)₁₀ = 1,2,3,5,7 [0,4,6]

В двоичном виде :

f(abc)₂ =001₂ V 010₂ V 011₂ V101₂ V111₂

СДНФ:

СКНФ:

Минимизируем ПФ по кубу соседних чисел:

111

101

011

110

010

001

100

000

Квадрат соответствует обобщенному коду – –1

Ребро соответствует обобщенному коду 01 –

Таким образом, ДНФ ПФ имеет вид : , т.е

Далее реализуем нашу ПФ схемой из функциональных элементов.

В базисе Вебба (И-НЕ):

:

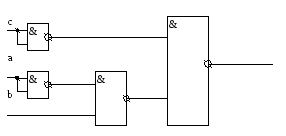
В базисе Шеффера (ИЛИ-НЕ)

:

1

1

1

b

1

a

c

Задание №2.

Дано: кодовая последовательность 0-1-3-2 двоичного двухразрядного сигнала.

Получить ПФ описывающие соответствующий конечный автомат-распознаватель последовательности:

a Z₁ "верно"

Входы Выходы

b Z₂ "неверно"

Последовательность поступает на входы a,b конечного автомата (КА):

20	a	0	0	1	1
21	b	0	1	1	0

Это правильная последовательность изменения входов a,b в соответствии с заданием.

Возможны и неправильные последовательности из алфавита {0,1,2,3}.

Ограничим возможные неправильные коды изменением только одного двоичного разряда .

Рассмотрим соответствующий квадрат соседних чисел:

11 (3)

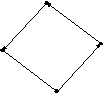
01 (1)

(2) 10

00 (0)

Направление изменения входных кодов показано стрелками. Видно, что в начале из 00 (0) имеем переход в 01 (1). Это если последовательность правильная. А если не правильная?

Тогда возможен лишь один вариант:

11 (3)

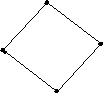
01 (1)

10 (2)

00 (0)

Из 00 в 10.

На втором шаге правильно: 01 (1) в 11 (3), а неправильно?

11 (3)

10 (2)

00 (0)

01 (1)

Т.е. назад, в 00.

Аналогично на третьем шаге неправильным будет переход из 11 (3) в 01 (1):

01 (1)

10 (2)

11 (3)

00 (0)

Таким образом, можно построить граф последовательностей:

правильные

неправильные

Т.е. имеем всего 4 последовательности

1) 0 – 1 – 3 – 2 (правильная)

2) 0 – 2

3) 0 – 1 – 0 неправильные

4) 0 – 1 – 3 – 3

Строим первичную таблицу переходов соответствующего конечного автомата - распознавателя последовательности 0 – 1 – 3 – 2 :

ПТП:

№ такта	ab				Z2	Z1
	00	01	11	10
1		2		5	0	0
2	6		3		0	0
3		7		4	0	0
4					0	1 последовательность принята !
5					1	0
6					1	последовательность нарушена ! 0
7					1	0

Здесь кружком обведены устойчивые такты работы автомата-распознавателя. Переход от одного устойчивого такта в соответствующей строке таблицы переходов – выходов к другому осуществляется через неустойчивый такт. Каждый устойчивый такт соответствует строке. Т.е. в ПТП в каждой строке только один устойчивый такт, номер которого равен номеру строки.

Можно получить переключательные функции и по ПТП, но в большинстве случаев пытаются сократить число строк ПТП ("сжать" ПТП), т.е получить минимизированную таблицу переходов (ТП)

Это удобно делать путем построения графа объединения строк. В таком графе число вершин равно числу строк ПТП. В нашем случае – 7. Ребром соединяются те вершины, которые соответствуют двум строкам, которые можно слить в одну строку; т.е. в этих строках клетки не противоречат друг другу. Такими клетками будут:

1) пустые клетки и клетки с цифрами и наоборот;

2) клетки с цифрой i и клетки с цифрой в кружке и наоборот, т.е. неустойчивый такт

и устойчивый соответствующий такты сливаются в один устойчивый

2

II

В

I

1

нашем случае:

3

7

III

4

6

5

Теперь в графе объединения строк необходимо выделить минимимальное количество максимальных подграфов.

Это количество и определяет число строк в минимизированной таблице переходов МТП. У нас в одну строку могут быть слиты (объединены) строки 3,4,6,7;

(1,5) , 2 - остается одна. Возможны другие варианты объединения. Но ни при одном варианте мы не получим две строки (это идеал – к нему надо стремиться).

Получим минимизированную таблицу переходов (МТП):

сливаемые строки	№ группы строк	ab
		00	01	11	10
1 , 5	I		2
2	II	6		3
3, 4, 6, 7	III

Приступим к кодированию состояний автомата. Применим соседние кодирование, которое характеризуется тем, что строки МТП, между которыми имеются переходы должны быть закодированы соседним кодом (кодом, отличающимся только в одном разряде).

Поэтому, с учетом того, что строки, в которой имеется первый такт ( ) кодируется нулями (исходное состояние), кодирование может имееть вид:

I : 00

II: 01

III: 11

Т.е. необходимо два разряда, которые обозначим y₁y₂. Это не что иное, как текущее состояние автомата, которое принято обозначать у₂(t) y₁(t) или сокращенно у₂(t) y₁(t) .

Теперь получим таблицу переходов-выходов (ТПВ), в которой указывается, как автомат переходит из текущего состояния – коды строки, в последующее – код в некоторой клетке при различных комбинациях входов ab: у₂(t+1) y₁(t+1) или сокращенно у₂y₁(t+1)

текущее состояние номер клетки

y2y1(t)	ab
	00	00	01	11
00	0	1	3	2
					последующие состояние
01	4	5	7	6
11	12	13	15	14

выходные сигналы

Код клетки – это соединение (конкатенация) двоичного кода строки и столбца, представленные в виде десятичного числа. Очевидно, что кружки в МТП и ТПВ располагаются в одинаковых клетках. Если такт устойчивый, то в кружке ТПВ в числителе указывается номер соответствующей строки. Если такт неустойчивый - то указывается код той строки, в которую осуществляется переход. В знаменателе указывают выходные сигналы z₂ z₁. Они берутся из первичной таблицы переходов – выходов. Так, если в МТП в клетке цифра 5 (пятый такт), то из пятой строки ПТП берется 10 (нарушение последовательности) и указываем это число в клетке 2 (0010)

Теперь получаем все четыре ПФ, описывающие наш автомат в символической форме:

^у2(t+1) y₂y₁ ab ^{= 4,7,12,13,15,14 [0,1,2,5],}

^у1(t+1) y₂y₁ ab ^{= 1,4,5,7,12,13,15,14 [0,2],}

^Z2 y₂y₁ ab ^{= 2,4,12,13 [0,1,5,7,15,14],}

^Z1 y₂y₁ ab ^{= 14 [0,1,2,4,5,7,12,13,15].}

По этим ПФ можно построить схему автомата, предварительно проведя минимизацию. Получим структурную схему автомата: