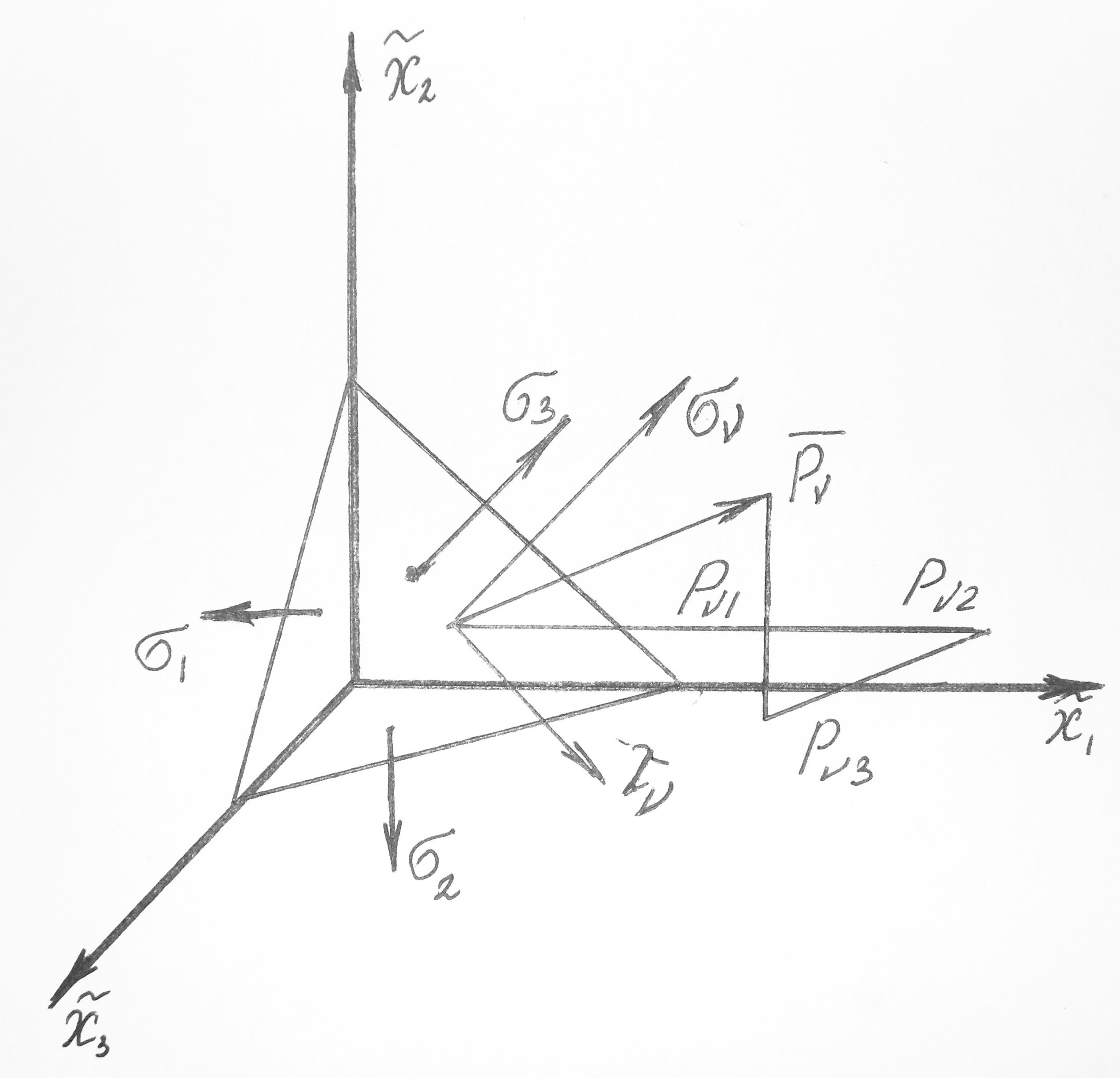
Эллипсоид Ламе
Пусть напряженное состояние в точке ДТТ характеризуется следующим тензором напряжений:
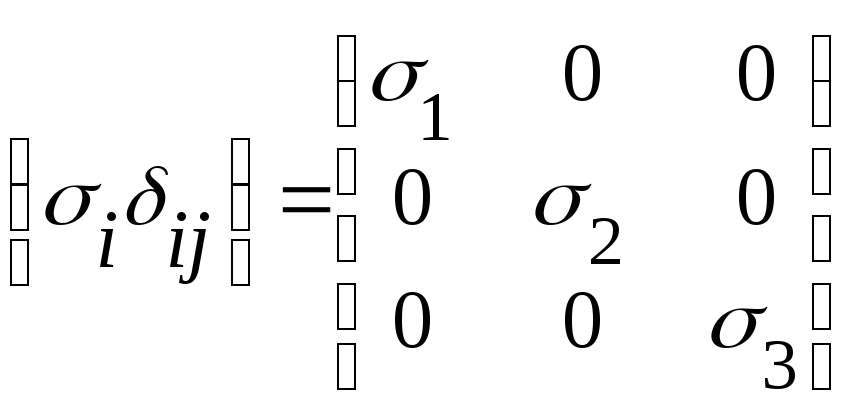
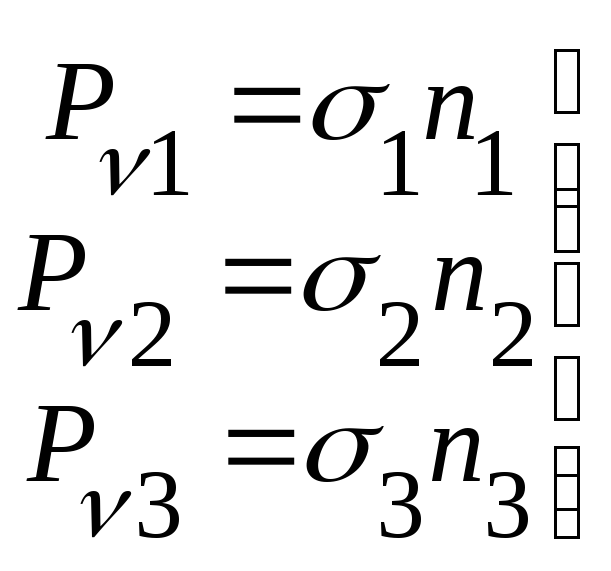- компоненты
вектора полного напряжения
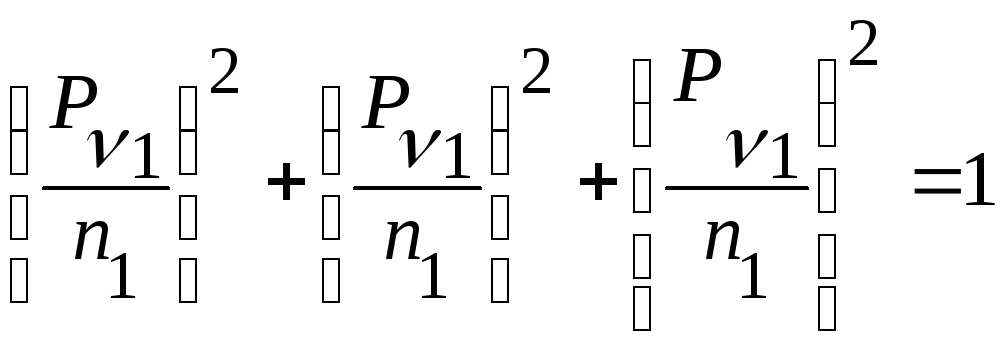- уравнение
поверхности второго порядка (эллипсоид
Ламе)
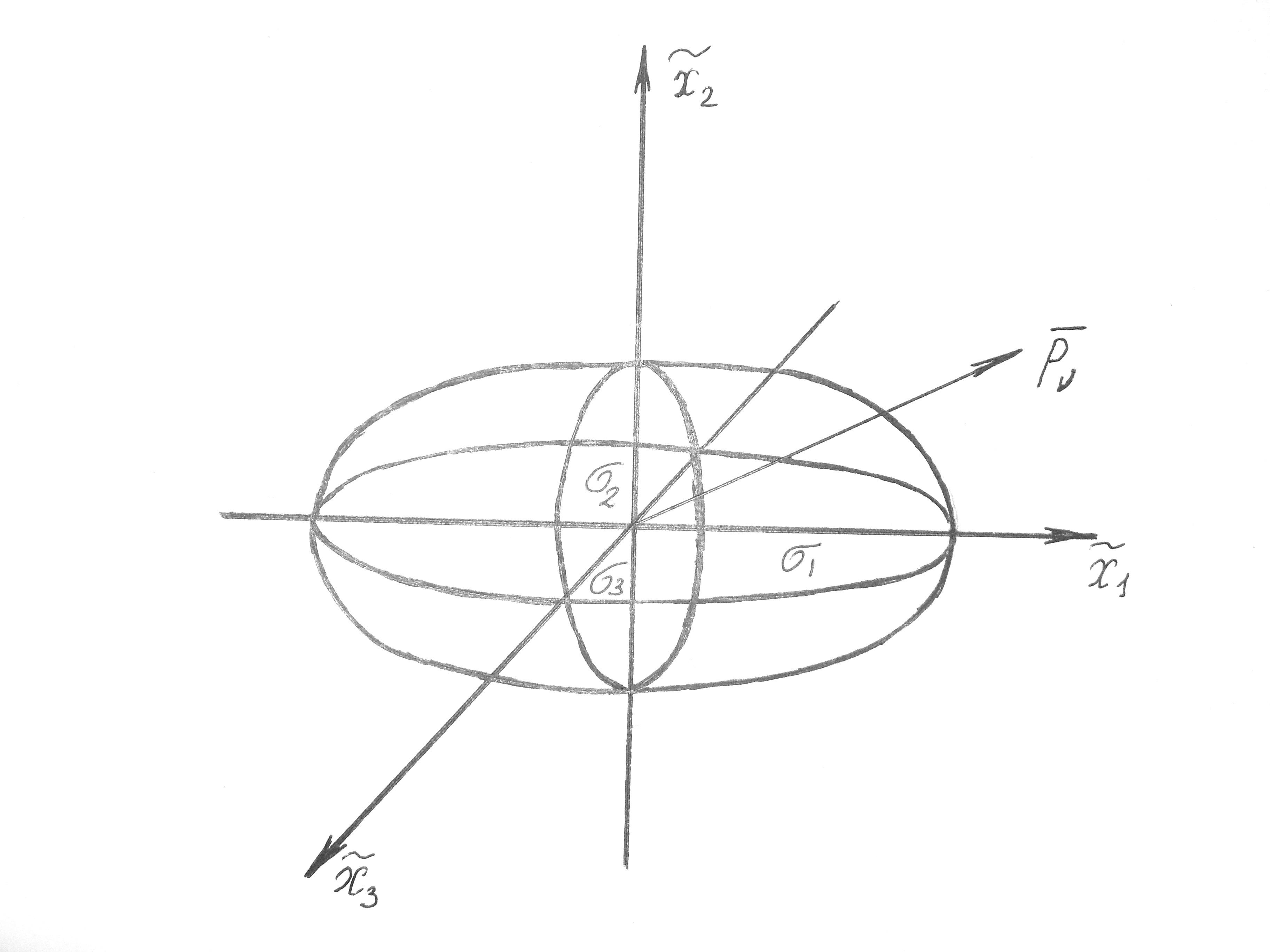
Характеризует
длины вектора полного напряжения при
непрерывном изменении ориентации
внешней нормали к площадке с центром
тяжести в рассматриваемой точке (конец
вектора полного напряжения в главных
осях
описывает эллипсоид с полуосями
).
Тензор напряжений может быть представлен в виде суммы двух тензоров:
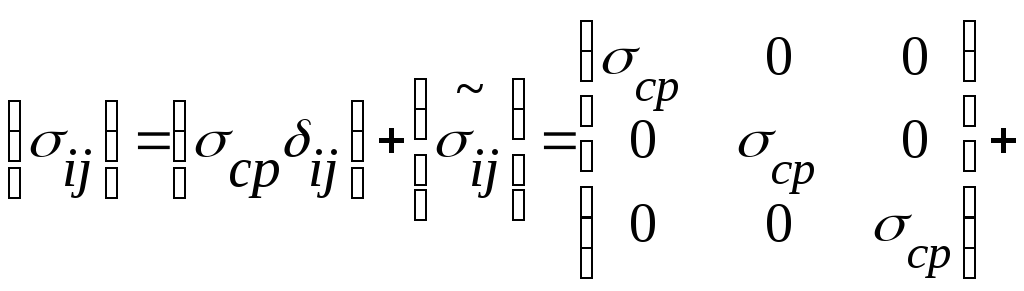
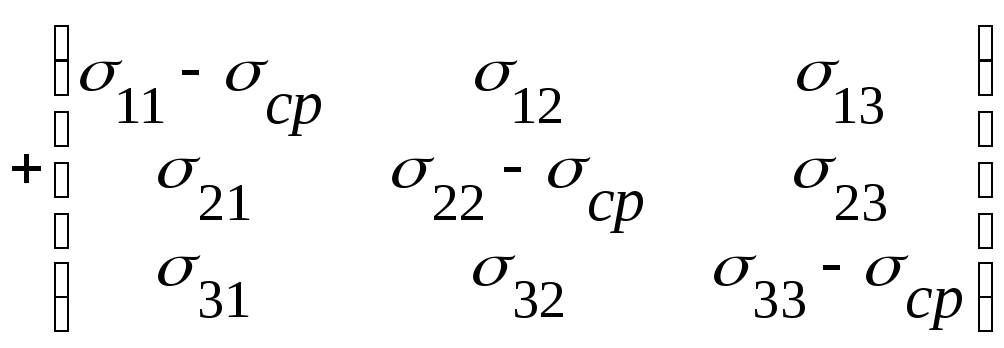
Первый тензор – шаровой тензор напряжений – характеризует напряженное состояние вызванное всесторонним растижением-сжатием.
Второй тензор – дивиатор напряжений – характеризует отклонение рассматриваемого напряженного состояния от всестороннего растижения-сжатия.
- первый инвариант
шарового тензора равен первому инварианту
тензора напряжений в рассматриваемой
точке.
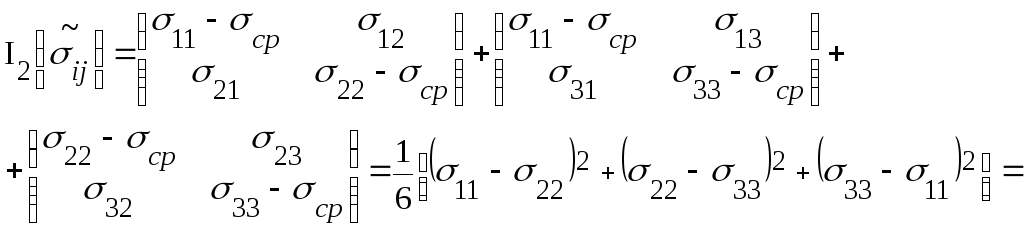
- второй инвариант
шарового тензора напряжений.
- модуль напряжений.
- интенсивность
нормальных напряжений.
- интенсивность
касательных напряжений.
Тензор напряжений позволяет ввести еще две характеристики (два инварианта) нормальных и касательных напряжений в октаэдрических площадках.
Октаэдрические площадки – это площадки равно наклоненные к главным осям, то есть:
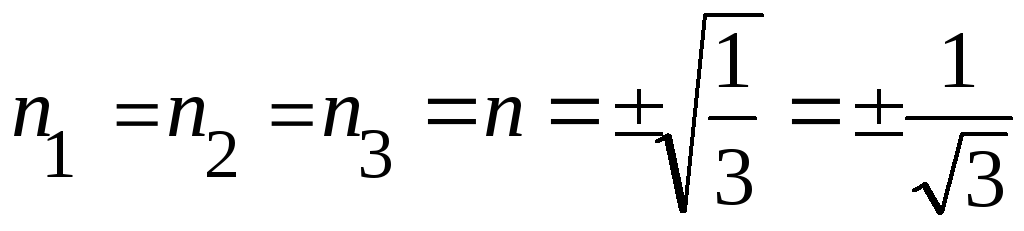
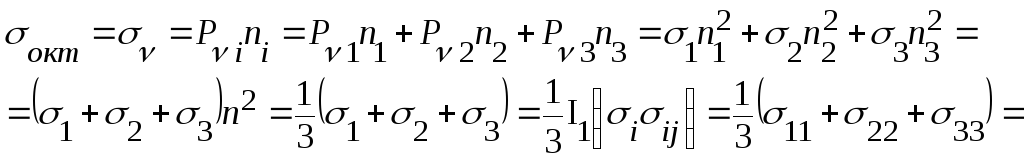
- нормальное
октаэдрическое напряжение.
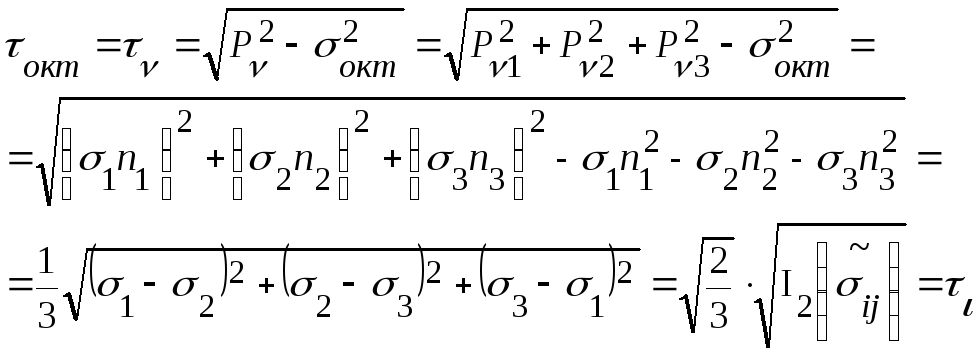
- касательное октаэдрическое напряжение.
По тензору напряжений могут быть найдены площадки, где касательные напряжения экстремальны и соответствующие им нормальные напряжения.
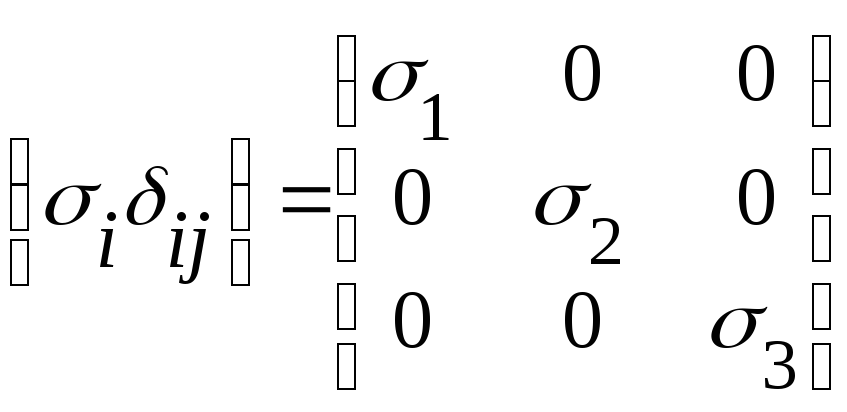
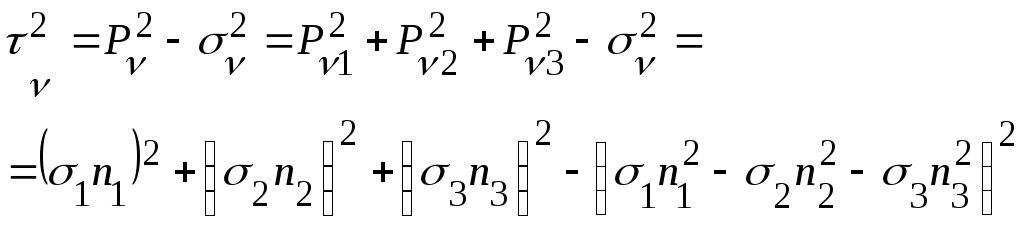
Для
и
справедливо:
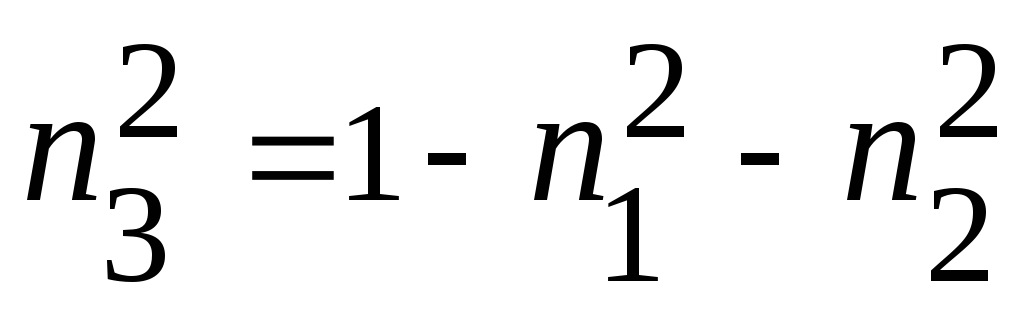
Тогда:
и
,
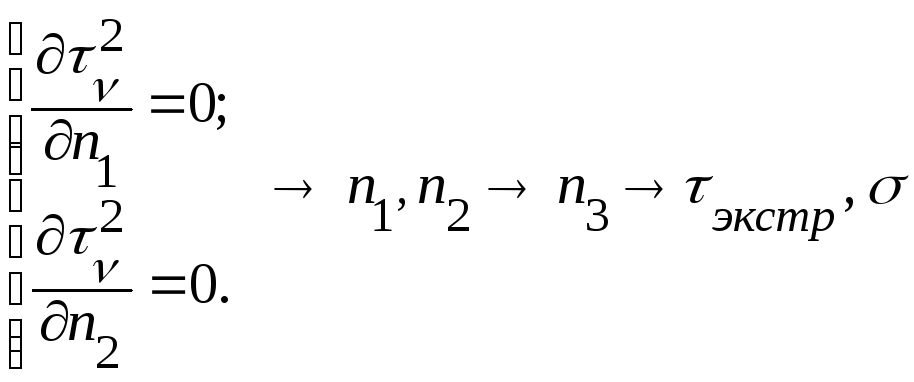аналогично:
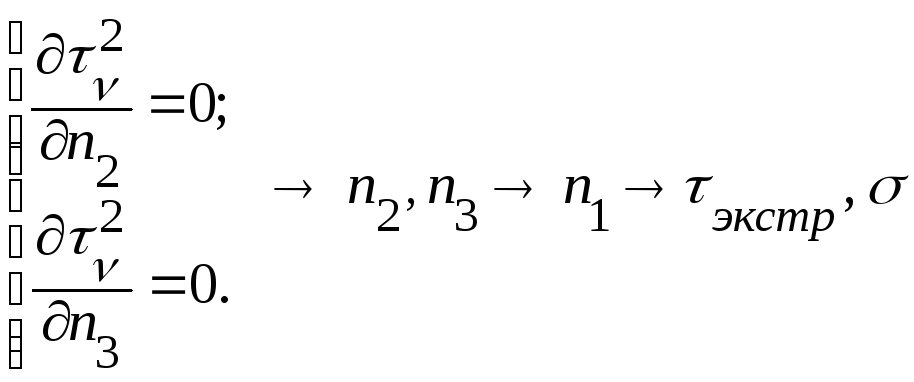
Анализируя шесть уравнений, находим шесть не повторяющихся групп направляющих косинусов, из которых последние три группы нас не устраивают, поскольку определяют положение площадок, где касательные напряжения равны нулю:
.
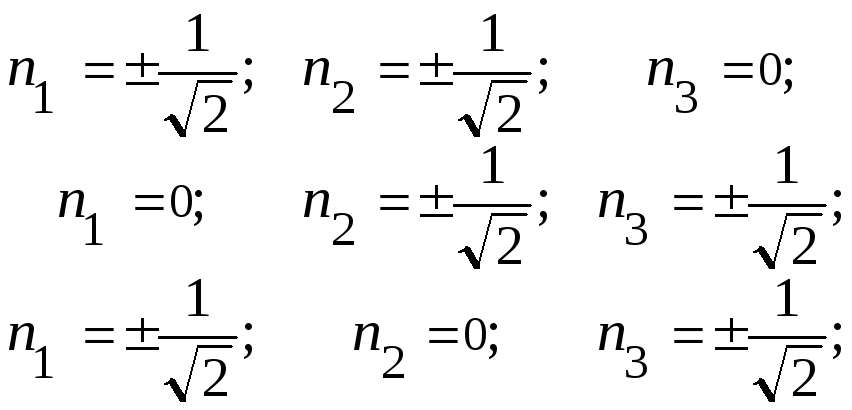
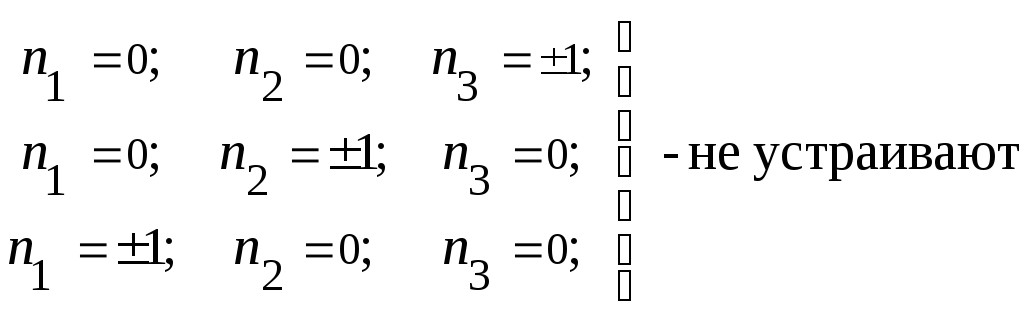Подставляем
найденные направляющие косинусы в
формулы для
и
с учетом (*), получаем формулы для
определения величины экстремальных
касательных напряжений и соответствующих
им нормальных напряжений:
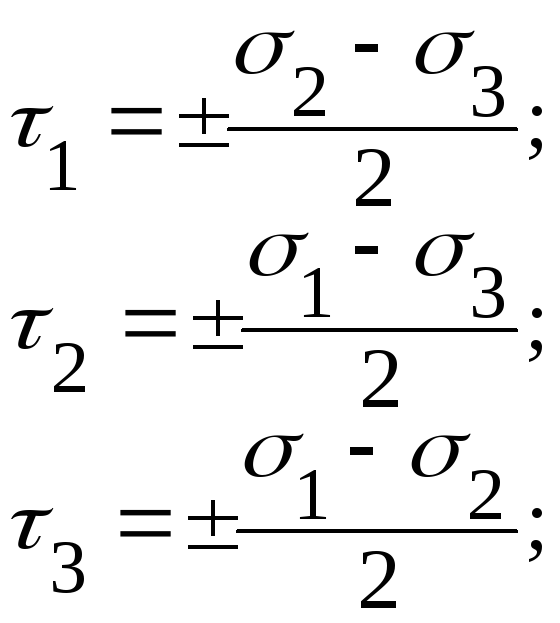
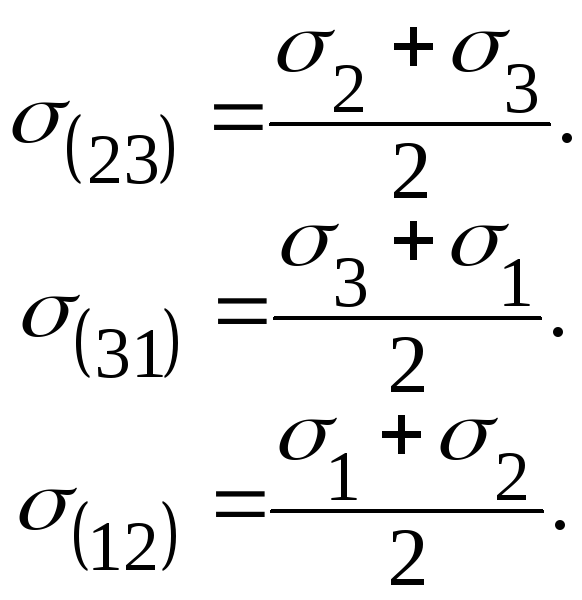
- действуют в
площадках параллельных соответственно
и делят угол между оставшимися главными
осями пополам.
Замечания:
Максимальные касательные напряжения с учетом
:
.
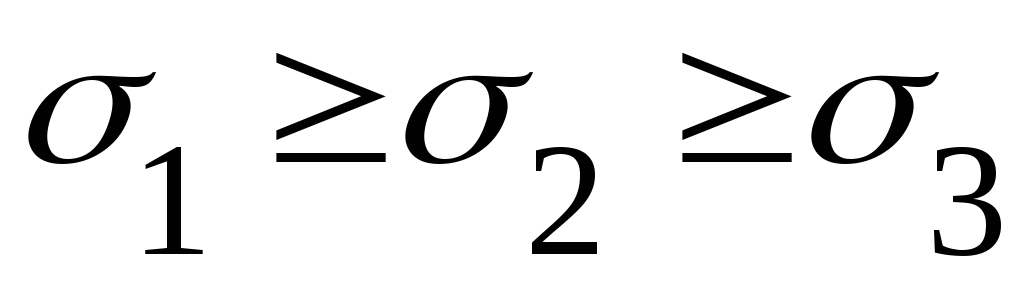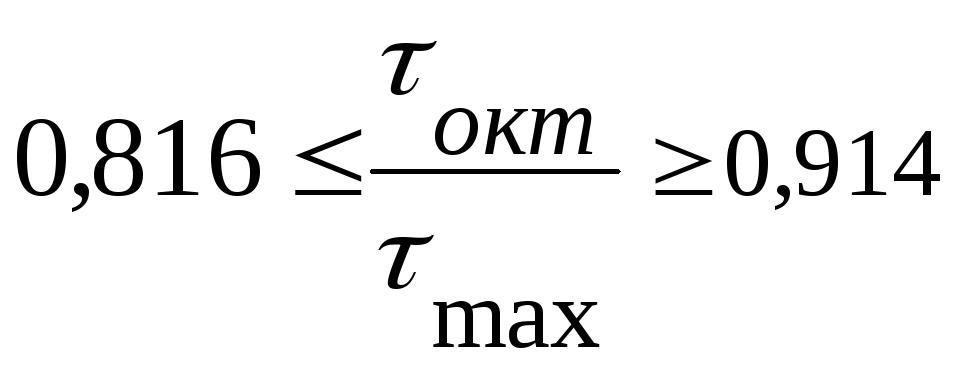
Компоненты тензора напряжений удовлетворяют уравнению равновесия:
;
- уравнение элементарного параллелепипеда
в окрестности любой точки внутри ДТТ.
;
- уравнение равновесия поворотного
тетраэдра.
,
- компоненты вектора интенсивности
внешних поверхностных сил.