Три способа представления вектора

1. Модулем или длиной и направляющими косинусами.

2. Проекциями или составляющими на координатной оси.

,

3. Нормальными и касательными составляющими или напряжениями, причем: ;.

Из рисунка видно, что .

Рассмотрим три взаимно перпендикулярные площадки в произвольной точке, причем внешние нормали к ней параллельны координатным осям:

Напряженное состояние в любой точке ДТТ известно, если известен тензор напряжений или совокупность нормальных и касательных напряжений действующих в площадках элементарного параллелепипеда выделенного в

окрестностях этой точки.

;

; - нормальное напряжение, действующее перпендикулярно

площадке в рассматриваемой точке или действующее в площадке внешняя

нормаль которой совпадает с направлением координатной оси.

;; - касательное напряжение, действующее в плоскости площадки с внешней нормалью.

, если направление напряжения и внешней нормали к площадке

одновременно или совпадает, или не совпадает с направлением координатных осей.

Уравнение равновесия элементарного тетраэдра

= 0

Преобразуем представленное выражение с учетом свойств симметрии тензора сопротивлений.

;;

Тогда:

= 0;

= 0;

= 0 ;

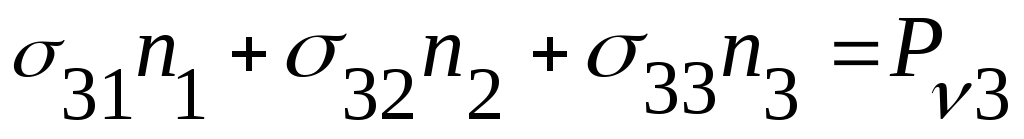
Или компактно:

;

Замечание: уравнение равновесия элементарного тетраэдра выделенного в окрестностях произвольной точки лежащей на поверхности ДТТ может быть получено аналогичным образом, они носят название – уравнения равновесия первого рода.

;

- i-я компонента вектора интенсивности внешних поверхностных сил.

Если в произвольной точке, лежащей на поверхности ДТТ, известны компоненты тензора напряжений, то в этой точке могут быть определены компоненты вектора интенсивности внешних поверхностных сил – смысл значения уравнения первого рода.

Уравнение равновесия элементарного параллелепипеда или уравнение равновесия второго рода.

Любое ДТТ представляет собой совокупность элементарных параллелепипедов и элементарных тетраэдров.

Для простоты изображения все виды напряжений покажем только центры тяжести площадок, причем учтем, что в объеме элементарного параллелепипеда по нарастающим координатам происходит увеличение напряжения на бесконечно малую величину.

Так как ДТТ под действием внешнего нагружения находится в равновесии, то и элементарный параллелепипед находится в равновесии.

Если мы представленное выражение преобразуем с учетом свойств симметрии тензора напряжений, то получим:

;

Или подробно:

= 0;

= 0;

= 0;

Замечания:

Уравнение равновесия второго рода позволяет по известным компонентам тензора напряжений в рассматриваемой точке лежащей внутри ДТТ компоненты ,вектор интенсивности внешних объемных сил в рассматриваемой точке.

Свойства тензора напряжений

1. Является тензором второго ранга, то есть содержит 3² = 9 компонентов.

2. Является симметричным, то есть ; ; .

Замечания:

1. Поскольку элементарные площадки малы, то нагрузки равномерно распределены по этим площадкам.

2. Моменты равнодействующих напряжений параллельные оси или ее пересекающие равны нулю.

Пренебрежем компонентами четвертого порядка: ; ;

.

Эти свойства известны, как закон парности касательных напряжений.

3. Если в любой точке ДТТ известны компоненты тензора напряжений, то в любой площадке с центром тяжести в этой точке и внешней нормалью к неймогут быть найдены:и.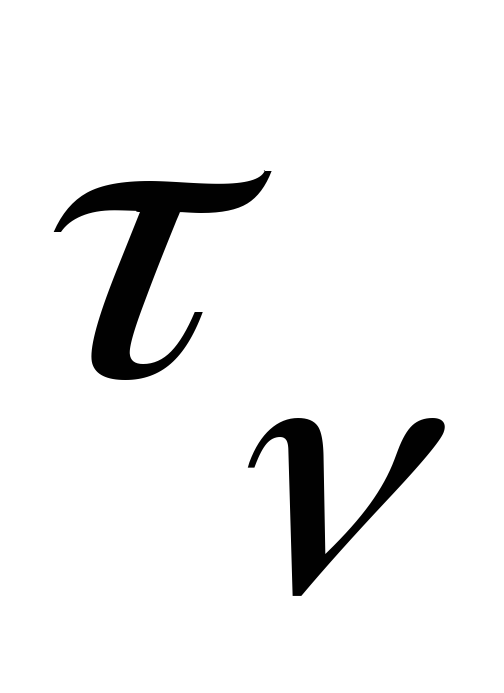

;

;

Состояние внешних поверхностных сил в рассматриваемой точке ДТТ:

4. Тензор напряжений всегда может быть приведен к диаграммному виду.

, где - экспериментальные нормальные напряжения.

Главные площадки – взаимно перпендикулярные площадки в которых касательные напряжения равны нулю, а нормальные напряжения экстремальны.

Внешние нормали к главным площадкам называются главными нормалями или направляющими (главными осями).

, ;

;

- контактная форма представления характеристической системы уравнений для определения величины главных напряжений и величин направляющих косинусов главных нормалей.

Поскольку направляющие косинусы не могут одновременно равняться нулю, следовательно в характеристической системе определитель равен нулю.

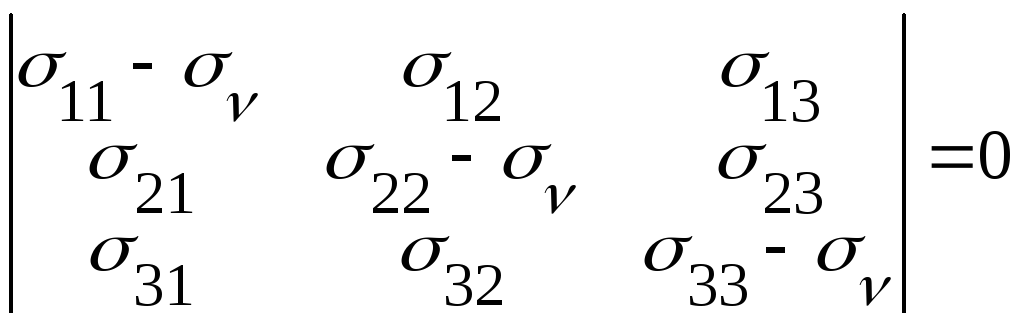или

Характеристическое уравнение для определения величин главных напряжений .

Для каждого главного напряжения определяются величины направляющих косинусов главных площадок.

5. Характеристическое уравнение может быть переписано в виде характеристического кубического уравнения, так как тензор напряжений имеет три инварианта (три характеристики зависящие от поворота системы координат):

- характеристическое кубическое уравнение, где:

-третий (кубический) инвариант тензора напряжений.

-

второй (кубический) инвариант тензора напряжений.

- первый (линейный) инвариант тензора напряжений.