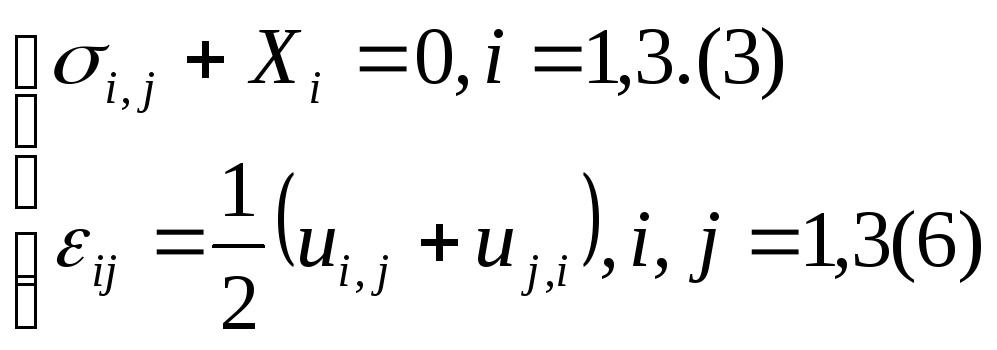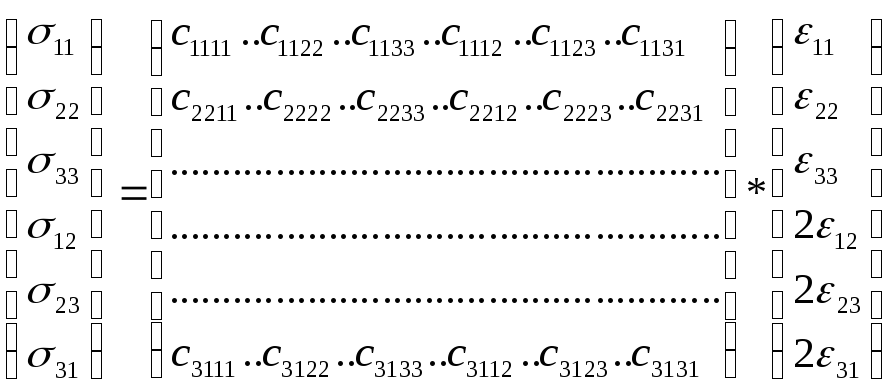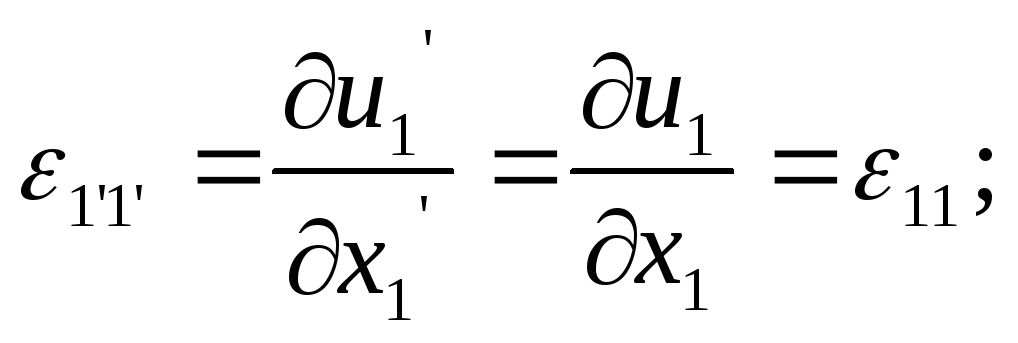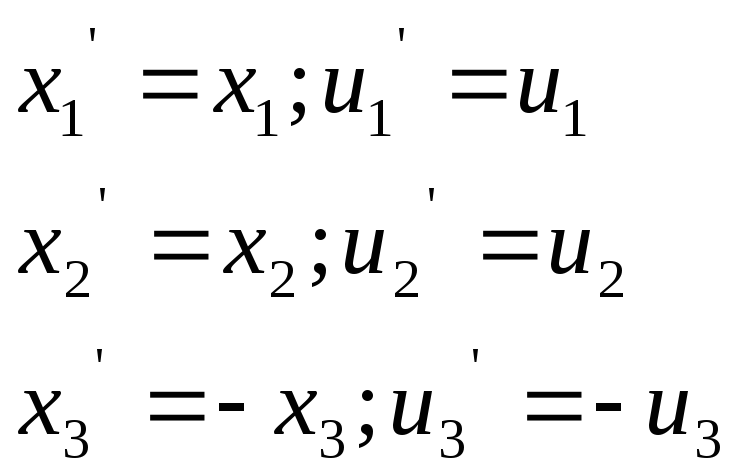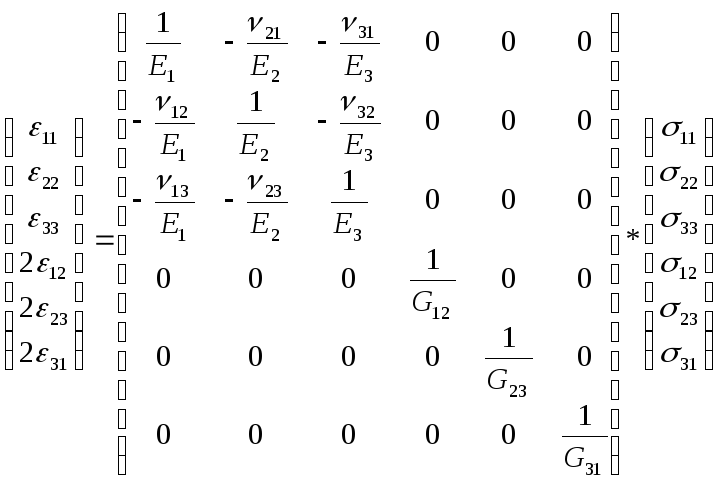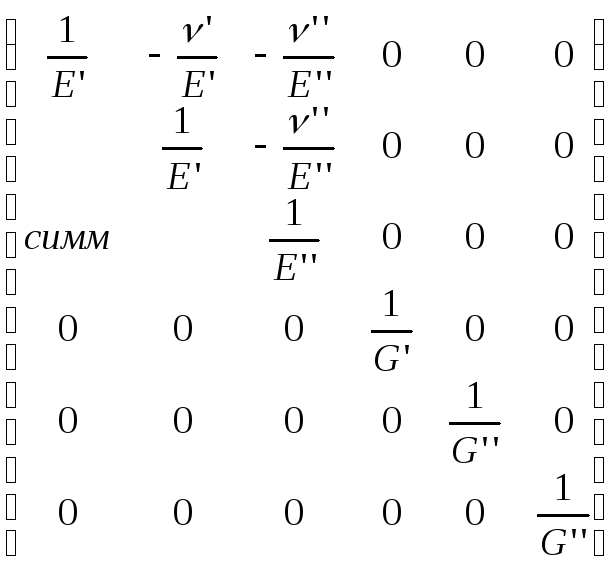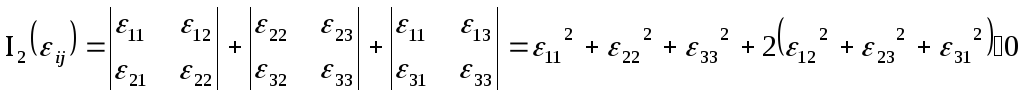ФДТТ1
.doc3 Связи между напряжениями и деформациями или физические зависимости.
В теории деформаций и в теории напряжений имеем дело с 15-ю функциями координат точек тела, а именно:
![]() i=1,3
–компоненты вектора перемещений (3);
i=1,3
–компоненты вектора перемещений (3);
![]() i,j=1,3
– компоненты тензора Коши или тензора
малых деформаций(6);
i,j=1,3
– компоненты тензора Коши или тензора
малых деформаций(6);
![]() i,j=1,3
– компоненты тензора напряжений(6).
i,j=1,3
– компоненты тензора напряжений(6).
Вывели 9 деформационных зависимостей для любой точки находящейся внутри деформированного твердого тела (дтт).
Уравнения равновесия элементарного параллелепипеда
|
|
(3.1) |
Хi – компоненты вектора интенсивности внешних объемных сил,
εij - дифференциальные зависимости Коши.
Система 9-ти дифференциальных уравнений является незамкнутой или недоопределенной должна быть заполнена зависимостями между напряжениями и деформациями. Они получаются в результате механических испытаний. Для разных материалов они разные. Взаимно-однозначная связь между напряжениями и деформациями называется законом упругости:
|
|
(3.2) |
или
|
|
(3.3) |
Причем состояние,
когда при нулевых аргументах функции
деформаций и функции напряжений равны
нулю, то есть
![]() называется естественным состоянием.
называется естественным состоянием.
Под действием внешнего нагружения твердое тело деформируется, то есть изменяет свои первоначальные размеры и формы, при снятии внешнего нагружения оно может восстанавливать свои первоначальные размеры и форму или, как говорят, деформация обратима; если не восстанавливает – деформация необратима.
Упругий потенциал. Линейный потенциал. Удельная дополнительная потенциальная энергия деформации. Потенциальная энергия деформации тела.
Рассмотрим одноосное или линейное напряженное состояние элементарного параллелепипеда выделенного в окрестности любой точке деформированного твердого тела.
|
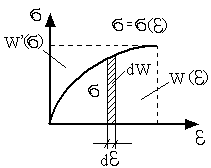
Нелинейное упругое тело (материал)
-упругий потенциал или удельная потенциальная энергия деформации или потенциальная энергия деформации элементарного параллелепипеда выделенного в окрестности рассматриваемой точки. Причем:
|
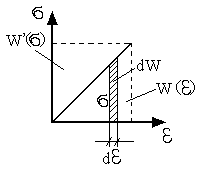
Линейно упругое тело (материал)
- линейный потенциал или потенциальная энергия линейно-упругого деформирования элементарного параллелепипеда в окрестности рассматриваемой точки деформированного твердого тела.
Формула Клапейрона
|
||||||||||
|
Удельная дополнительная потенциальная энергия |
|||||||||||
характеристика немеющая механического смысла определяемая представленным образом; равняется площади под кривой
|
удельная дополнительная потенциальная энергия и линейный потенциал совпадают по величине.
|
||||||||||
|
Рассмотрим медленное или статическое многократное нагружение элементарного параллелепипеда в окрестности произвольной точки деформированного твердого тела |
|||||||||||
|
Повторяющиеся индексы представляют собой суммирование. Причем W(0)=0, если известен упругий потенциал W(εij) то напряжения могут быть найдены по формуле Грина:
|
формула Клапейрона
|
||||||||||
|
П= |
(3.15) |
||||||||||
- потенциальная энергия деформации тела.
Закон Гука.
Для одноосного напряженного состояния связь между напряжением и деформацией была получена экспериментально в 1660 году английским физиком-математиком Робертом Гуком.
|
σ=Еε |
(3.16) |
- закон Гука для однородного изотропного тела при линейно напряженном состоянии Е=const
Закон Гука для ЛНС может быть распространен и на многократное напряженное состояние с учетом следующих гипотез:
-
Гипотеза относительной жесткости
εij<<1, а перемещение точек тела меньше его размеров.
-
Гипотеза о естественном состоянии
-
Принцип суперпозиции
Эффект от суммы деформаций равняется сумме эффектов от каждой деформации
|
|
(3.17) |
-
Гипотеза сплошности
согласно которой функции деформаций (аналогично напряжений) являются непрерывными функциями и в окрестности естественного состояния могут быть разложены в ряд Тейлора, то есть
|
|
(3.18) |
|
|
(3.19) |
|
|
(3.20) |
тензорная форма представления закона Гука, где
-
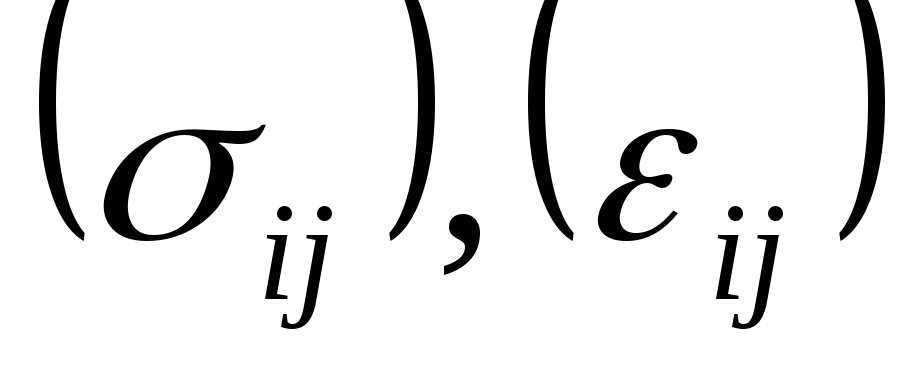 - тензоры второго
ранга, соответственно, напряжений и
деформаций, содержат 32=9
компонент, из которых 6 являются линейно
независимыми.
- тензоры второго
ранга, соответственно, напряжений и
деформаций, содержат 32=9
компонент, из которых 6 являются линейно
независимыми. -
 (
(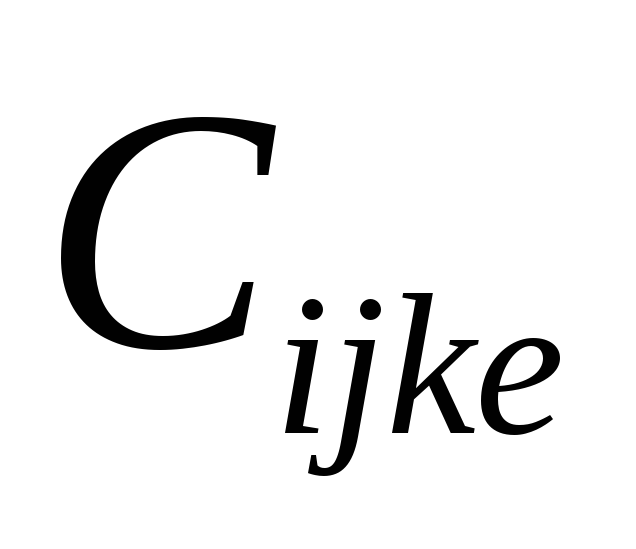 ),
(
),
(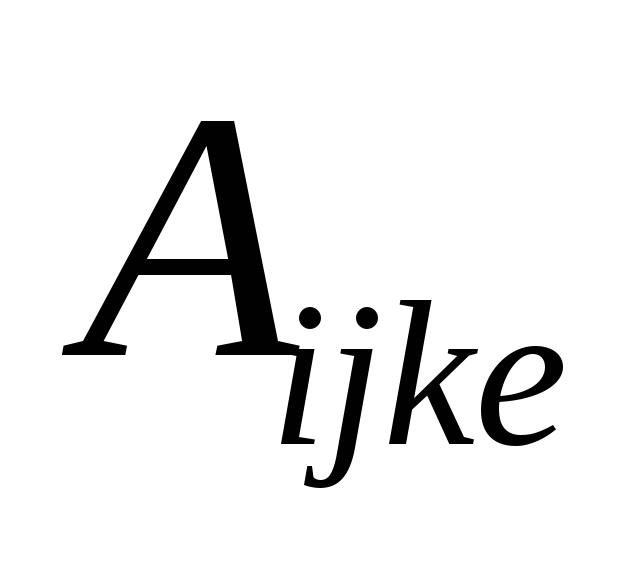 )
– тензоры четвертого ранга, соответствующие,
коэффициентам жесткости или упругости
и податливости 34=81
компонент, из которых в силу симметричности
тензоров напряжений и деформаций
линейно независимыми являются 36.
)
– тензоры четвертого ранга, соответствующие,
коэффициентам жесткости или упругости
и податливости 34=81
компонент, из которых в силу симметричности
тензоров напряжений и деформаций
линейно независимыми являются 36.
Существует также векторно-матричная форма представления закона Гука. Формально выглядит следующим образом:
|
|
(3.21) |
или
|
|
(3.22) |
|
1 2 3 |
(3.23) |
1 – вектор напряжений;
2 – матрица коэффициентов жесткости или упругости (6х6), является симметрично относительно главной диагонали, т. е. из 36 коэффициентов линейно независимыми являются 21 коэффициент;
3 – вектор деформаций.
![]()
Однородное тело
– тело (материал, среда), у которого
упругие свойства не зависят от координат
точек тела, то есть являются постоянными
величинами (![]() =соnst).
Неоднородное тело – тело, упругие
свойства которого зависят от координат
точек тела (
=соnst).
Неоднородное тело – тело, упругие
свойства которого зависят от координат
точек тела (![]() =
=![]() (х1х2х3х4),
Е=Е(х1х2х3)).
Изотропное (анизотропное)тело – тело,
у которого упругие свойства не зависят
от направления в любой точке (зависят
от направления).
(х1х2х3х4),
Е=Е(х1х2х3)).
Изотропное (анизотропное)тело – тело,
у которого упругие свойства не зависят
от направления в любой точке (зависят
от направления).
Замечания:
-
Тело может быть однородным или неоднородным и одновременно изотропным или анизотропным.
-
Если оси ЛСК совпадают с осями упругой симметрии тела (оси относительно которых свойства материала или тела являются симметричными или одинаковыми),то число коэффициентов жесткости или податливости являющихся линейно независимыми, становятся меньше, так как некоторые из коэффициентов зануляются, а некоторые являются одинаковыми.
Рассмотрим одну плоскость упругой симметрии, например:

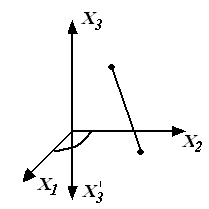
Тогда упругий потенциал должен быть инвариантен к преобразованию вида:
|
|
(3.24) |
то есть коэффициенты матрицы жесткости или податливости стоящие перед деформациями, меняющими знак должны быть равны нулю, а это коэффициенты у которых индекс 3 встречается 1-3 раза.
|
|
(3.25) |

|
|
(3.26) |
|
|
(3.27) |
то есть матрица коэффициентов жесткости имеет вид:
|
|
(3.28) |
13 линейно независимых коэффициентов
Две взаимно перпендикулярные плоскости упругой симметрии: х1х2 и х2х3.
Упругий потенциал должен быть инвариантен по отношению к следующему преобразованию:
|
|
(3.29) |
Чтобы инвариантность выполнялась необходимо, чтобы занулялись коэффициенты, у которых индекс 2 и 3 встречались 1 или 3 раза, то есть матрица коэффициентов жесткости (аналогично податливости) имеет вид:
|
|
(3.30) |
9 линейно независимых коэффициентов
Замечания:
-
Если тело имеет 2 взаимно перпендикулярной плоскости взаимной упругости, то третья им перпендикулярная тоже является плоскостью упругой симметрии, так как коэффициенты жесткости, у которых индекс «1» встречается 1 или 3 раза тоже зануляются.
-
Тело или материал, у которого есть 3 взаимно перпендикулярные плоскости упругой симметрии свойства, которых описываются 9-ю линейно независимыми коэффициентами, называются артотропным телом или материалом.
-
В отличие от матриц векторов компоненты тензора могут быть получены в новых повернутых осях через соответствующие компоненты этого тензора в старых осях и направляющие косинусы новых осей к старым осям.
|
|
(3.31) |
а коэффициенты векторов матриц в новых повернутых осях будут совершенно другими.
4) Закон Гука в тензорной форме используется для различных видов анализа связанных с поворотом координатных осей.
Закон Гука в векторно-матричной форме через технические модули.
Технические модули являются более доступными в плане их экспериментального явления по сравнению с коэффициентами жесткости, податливости.
Виды технических модулей описания упругих свойств анизотропного тела:
Ei – модули продольной упругости в направлении оси Хi или способность материала сопротивляться растяжению – сжатию в направлениях Хi.
Gij – модуль сдвига в плоскости оси ХiХj или способность материала сопротивляться сдвигу в плоскости ХiХj.
νij – коэффициент Пуассона или коэффициент поперечной деформации тили отношение относительной поперечной деформации к относительной продольной деформации при действии нормального в направлении Хi оси.
|
|
(3.32) |
νij,к – коэффициент взаимного влияния первого рода, характеризует способность материала накапливать относительную линейную деформацию в направлении оси Хк, при действии касательного напряжения σij в плоскости осей Хi Хj/
νi,jк – коэффициент взаимного влияния второго рода, характеризует способность материала накапливать относительную угловую деформацию в плоскости осей Хj Хк при действии нормального напряжения σi в направлении оси Хi.
ηij, kl – коэффициент Ченцова, характеризует способность материала накапливать относительную угловую деформацию в плоскости осей Хк Хl при действии только касательного напряжения в плоскости осей ХiХj.
Замечания:
-
Второй индекс или индексы после запятой означают деформацию, которая закрепляется в каждой строке матрицы коэффициентов податливости.
-
Первый индекс или индексы до запятой означают напряжения, вызывающие соответствующую деформацию.
|
1 2 3 |
(3.33) |
1 – вектор деформаций;
2 – матрица коэффициентов податливости через технические модули;
3 – вектор напряжений.
|
|
(3.34) |
36 ненулевых коэффициентов для описания упругих свойств анизотропного тела. Из них линейно независимыми являются 21 с учетом следующих 15 свойств симметрии:
![]() - 3 уравнения
- 3 уравнения
![]() - 3 уравнения
- 3 уравнения
![]() - 6 уравнений
- 6 уравнений
Первый блок характеризует изменение объема элементарного параллелепипеда выделенного в окрестности произвольной точки деформированного твердого тела при действии только нормальных напряжений.
Второй блок характеризует изменение объема при действии только касательных напряжений.
Третий блок характеризует изменение формы при действии только нормальных напряжений.
Четвертый блок характеризует изменение формы при действии только касательных напряжений.
Артотропный материал.
Матрица коэффициентов податливости через механические модули для него имеет вид:
|
Матрица податливости |
(3.35) |
Справедливы следующие свойства симметрии:
![]() - 3 уравнения
- 3 уравнения
Свойства артотропного материала могут быть описаны 9-ю линейно независимыми модулями :E1,E2,E3,G12,G23,G31 в соответствующих плоскостях; ν12, ν23, ν31. Остальные могут быть найдены по свойствам симметрии.
Трансверсально-изотропный материал. (Моноторопный, транстропный)
Это материал который является изотропным в одной из плоскостей. Например Х1Х2, в других перпендикулярных этой плоскости плоскостях является артотропным.
Матрица податливости для него имеет вид:
|
|
(3.36) |
Свойства его описываются 5-ю линейно независимыми модулями: E’, E’’, G’’, ν’, ν’’.
|
|
(3.37) |
Изотропный материал.
Матрица податливости через механические модули имеет вид:
|
|
(3.38) |
Свойства могут быть описаны 2-мя линейно независимыми модулями Е, ν.
|
|
(3.39) |
Примеры типов материалов.
-
Бетон, армируемый в 3-х направлениях железными прутками – артотропный материал.
-
Пластик, армируемый в одном направлении стеклянными волокнами или одномерно армируемый стеклопластик – трансвертально-изотропный материал.

Стеклопластик Железобетон
-
Обычные материалы и сплавы: сталь45, дюралюминий являются изотропными материалами.
Из физики кристаллов пришла двухиндексная схема значений, с помощью которой закон Гука может быть записан следующим образом:
σ11= σ1; σ22= σ2, σ33= σ3; σ12= σ4; σ23= σ5; σ31= σ6;
ε11= ε1; ε22= ε2; ε33= ε3; ε12= ε4; ε23= ε5; ε31= ε6.
|
|
(3.40) |
или
|
|
(3.41) |
Векторно-матричная форма закона Гука с использованием 2-х индексной системы обозначений.
В развернутой форме:
|
|
(3.42) |
![]() - свойство симметрии.
- свойство симметрии.
Из 36 ненулевых коэффициентов жесткости линейно независимыми являются 21, для материала общего вида анизотропии.
![]() .
.
Закон Гука в векторно-матричной форме через параметр Ламе для изотропного материала.
Может быть получен из закона Гука связывающего напряжение и деформации через механические модули с использованием параметров Ламе.
μ=G – модуль сдвига.
|
|
(3.43) |
|
|
(3.44) |
где
![]() - относительная объемная деформация.
- относительная объемная деформация.
или в развернутой форме:
|
|
(3.45) |
или другая эквивалентная форма представления деформации через напряжения.
|
|
(3.46) |
|
|
(3.47) |
- среднее или гидростатическое напряжение.
|
|
(3.48) |
- объемный модуль упругости или модуль всестороннего растяжения – сжатия.
Замечания:
-
Параметр Ламе для однородного материала является постоянными величинами для неоднородного материала, зависят от координат точек материала заполняющего объем тела.
-
Линейный потенциал для изотропного материала может быть представлен в виде квадратичной функции первого или второго инвариантов тензора Коши.
|
|
(3.49) |
|
|
(3.50) |
|
|
(3.51) |
3. Линейный потенциал для изотропного тела
W > 0 при λ>0, то есть E > 0, G > 0, k > 0, 0 < ν < 1/2.