Относительная объемная деформация. (Коэффициент кубического(всестороннего) растяжения-сжатия. Средняя относительная деформация.

Рассмотрим элементарный параллелограмм в главных осях,до деформации и после деформации.

-до деформации

-после деформации

- относительная объемная деформация

- относительная средняя деформации.

Относительная линейная деформация.

Длина(модуль) опр - ся константой-К и относительной линейной деформациив направлении.

,тогда подставив в формулу для ,направление касательной определено.

,с учетом формулы ,после преобразований получим уравнение поверхности 2-го порядка или уравнение поверхности деформации Коши:

в исходных осях

в главных осях

В Зависимости от величин и знаков главной деформации(аналогично деформации в исходных осях),различают следующие уравнения поверхности Коши:

А) Эллипсоид

Б)Однополостный гиперболоид

В)Двуполостный гиперболоид

6.Тензор малой деформации(тензор Коши) может быть представлен в виде суммы 2-х тензоров.

-шаровой тензор деформации характеризует относительное изменение объема элементарного параллелепипеда, выделенного в окрестности любой точки ДТТ без изменения формы.

Изменение V при всестороннем растяжении-сжатии элементарного параллелепипеда.

-девиатор деформации характеризует относительные изменения формы элементарного параллелепипеда без изменений V или отклонения рассматриваемого деформированного состояния в произвольной точке ДТТ, от деформированного состояния растяжения-сжатия элементарного параллелепипеда в этой точке.

- 1-й инвариант девиатора деформации

-2-й инвариант девиатора деформации

-модуль деформации(положительная величина, определенным

-интенсивность деформации сдвига

-интенсивность деформации

Замечание:

-используются при выводе основных зависимостей теории упругости,теории пластичности.

7.Компоненты тензора Коши удовлетворяют тождествам Сен-Винана или условием (уравнением) совместимости(непрерывности) деформации.

Получаются путем дифференциальных зависимостей Коши и исключающие перемещений

-уравнение совместимости деформации 1-го рода

Или

Другие две формулы могут быть получены с использованием правила круговой перестановки.

-уравнение совместимости 2-го рода(тождество)

Геометрический смысл тождеств Сен-Венана.

Выполнение тождеств означает, что между элементарными объемами(параллелепипедами, тетраэдрами)отсутствуют зазоры, пустоты, что для тела находящегося под действием внешнего нагружения означает, что оно не разрушалось.

Энергетический смысл:

Выполнение тождеств означает, что телом накоплено минимум потенциальной энергии деформации.

Определение перемещений в любой точке деформированного твердого тела при выполнении зависимости Коши и тождества Сен-Венана.

По известным компонентам тензора Коши.

Дано:

в любой точке ;

Определить:

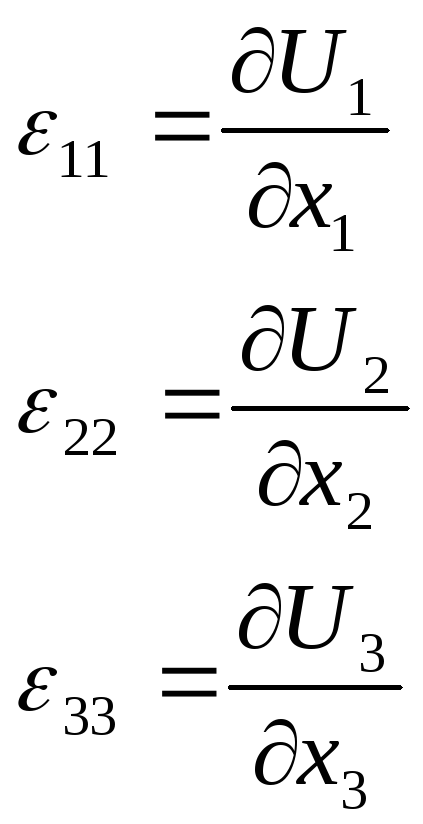- относительная линейная деформация

-относительная угловая деформация

-компонента вектора относительного перемещения;

-компоненты тензора дисторсии;

-компоненты вектора определяющего положение бесконечно близкой точки по отношению к рассматриваемой т.ДТТ

,т.к. справедливо тождество Сен-Венана,то первая компонента вектора перемещения может определяться следующим образом:

Криволинейный интеграл может быть расписан в виде суммы 3-х интегралов по прямым параллельным соответствующим координатным осям

и не пересекает границ тела.

Прежде, чем мы научимся определять компоненты вектора перемещения в любой точке, нам необходимо научиться определять частную производную от них по Лагранжевым координатам.

Используя в предыдущей формуле замену на

Замечание:

1.Подинтегральное выражение АВС через известные компоненты тензора Коши рассматриваемой точки ДТТ.

2.Частная производная может быть найдена через известные компоненты тензора Коши.

3.Частная производная может быть найдена аналогичным образом,через известныев рассматриваемой точке.

4.Можно показать, что справедливы условия Коши-Римана для подинтегральных выражений АВС:

т.е. АВС является частными производными одной и той же функции.

и является полным дифференциаломи криволинейный интеграл по пути движения отдо,не зависит от пути интегрирования.

Используя предыдущее замечание, первую компоненту вектора перемещения в точке, может определяться по формуле:

2,3 –компоненты вектора перемещений в рассматриваемой точке,могут быть определены по формуле аналогично формуле для U,или с использованием круговой подстановки.

в рассматриваемой т.ДТТ определяется с точностью до 9 знака интегрирования.

-линейной перемещение точки вызванное линейным перемещением параллельным соответствующим осям движения тела,как абсолютно твердого целого.

-угловые перемещения соответствующих элементов ,вызванными угловыми перемещениями тела, как абсолютно жесткого или твердого целого, причем с учетом справедливости зависимости (*) в естественном состоянии линейно-независимых, считается например:

-линейно-независимые интегралы

Итак:

1.По известным компонентам тензора Коши рассматриваемой точки с учетом справедливости зависимости Коши,тождеств Сен-Венана,могут быть определены компонентами вектора перемещенияс точностью до 6 знака линейно-независимых постоянных интеграла.

2.Постоянное интегрирование характеризует способ прикрепление координатных осей к телу не вызывают появление реактивнх сил и моментов,обычно принимают равным нулю.

3.В тождестве Сен-Венана является необходимым и достаточным условия интегрирования зависимости Коши для односвязных тел(тел без вырезов пустот)

4.Для многосвязных тел, связность = числу вырезов или пустот +1.В тождестве Сен-Венана должны быть дополнительные условиями характеризующими однозначность и непрерывность перемещений для точек лежащий на воображаемой разрезе:

Если вырезов в теле несколько,то должно быть несколько дополнительных условий,характеризующих непрерывность перемещений для точек воображаемых разрезов.

-замкнутые контуры охватывающие разрезы.