
ФБГОУ ВПО «Башкирский государственный аграрный университет»
Факультет___________ФПС______________
Кафедра Кадастра_недвижимости_ и_геодезии
Специальность_______ЗУК_______________
Форма обучения___________Очная_________
Курс _______________201/2______________
Каримов Динис Акрамович
РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА
По геодезии
На тему «ОБРАБОТКА РЕЗУЛЬТАТОВ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ»
«К защите допускаю»
Руководитель:
___Стар.преподаватель_______
__Яковлева Юлия Николаевна_
_____________________
«____» _____________ 2014г.
Оценка при защите:
____________________________
____________________________
(подпись)
«____»_________________ 2014г
УФА-2014
ОГЛАВЛЕНИЕ
-
ОБЩИЕ СВЕДЕНИЯ.....................................................................................3
2. ОБРАБОТКА РЕЗУЛЬТАТОВ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ.............4
-
ОПРЕДЕЛЕНИЕ НЕВЯЗОК..........................................................................7
-
Задача1……………………………...........................................................7
-
Задача 2.....................................................................................................8
-
3.3 Задача 3…………………………………………………........................8
ЗАКЛЮЧЕНИЕ..................................................................................................11
БИБЛИОГРАФИЧЕСКИЙ СПИСОК..............................................................12
-
Общие сведения
Под равноточными измерениями понимают однородные результаты, полученные в процессе измерений инструментами одного класса точности при одинаковых условиях. Измерения в свою очередь бывают: необходимые и избыточные.
В геодезической практике всегда выполняют некоторое число избыточных измерений с тем, чтобы обеспечить контроль, повысить точность и получить сравнительные данные для оценки точности полученного результата.
В процессе измерений участвуют наблюдатель, приборы и условия внешней среды, которые постоянно меняются, что и приводит к неизбежным погрешностям измерений.
Случайные погрешности неустранимы и неизбежны.
Для случайных ошибок установлены следующие свойства:
а) случайные ошибки для данных условий не могут превышать по абсолютной величине известного предела;
б) малые по абсолютной величине ошибки появляются чаще больших;
в) по знаку положительные ошибки появляются так же часто, как и равные им по величине отрицательные ошибки;
г)
среднее арифметическое из случайных
ошибок одной и той же величины неограниченно
стремится к нулю с увеличением числа
измерений. Это свойство можно записать
так:

где ∆ – случайная ошибка; n – число измерений.
-
Обработка результатов равноточных измерений
Среднее
арифметическое значение или арифметическая
средина вычисляется:
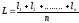 =
=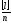
Для
упрощения вычисления арифметической
срединой вводят приближенное значение
измеряемой величины
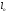 .
Выбрав приближенное значение, вычисляют
остатки
.
Выбрав приближенное значение, вычисляют
остатки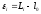 .
.
Приближенное
значение
 выбирается
так, чтобы остатки
выбирается
так, чтобы остатки
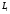 были
малы. Иногда за
были
малы. Иногда за
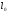 принимают наименьшее значение
принимают наименьшее значение
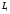 или
округленный результат измерения. Тогда
формула арифметической срединой через
приближенное значение:
или
округленный результат измерения. Тогда
формула арифметической срединой через
приближенное значение:
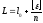 .
.
В
случае, когда из результатов измерений
получено среднее арифметическое
значение, вводят вероятнейшие поправки:
 =
= ,
которые так же используются для контроля
вычислений: [
,
которые так же используются для контроля
вычислений: [ ]=-[υε]+(
]=-[υε]+(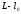 )[υ]
)[υ]
Средняя
квадратическая погрешность,
вычисляется
по формуле: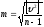 .
.
Средняя
квадратическая погрешность арифметической
средины находится по формуле:

Если
каждая из велечин измерена дважды и все
измерения равноточные, то средняя
квадратическая погрешность одного
измерения определяемая по разностям
двойных равноточных измерений
 =
L’-L’’,
определяется по формуле:
=
L’-L’’,
определяется по формуле:
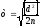 .
.
В том
случае, когда в разностях есть
систематические погрешности θ
 ,
то их исключают: ∂=
,
то их исключают: ∂= -θ
и получают формулу средней
квадратической погрешности арифметической
средины:
-θ
и получают формулу средней
квадратической погрешности арифметической
средины:
 .
.
Контролем вычислений служат следующие формулы:
[∂]=0;
[∂ ²]=[ ∂]
∂]
[∂²]=[ ²]-
θ[
²]-
θ[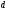 ]=[
]=[ ²]-[
²]-[ ²]/n
²]/n
3 Решение задач
3.1 Задача 1
Найти среднюю квадратическую погрешность суммы углов n-угольника, если углы измерялись с точностью.
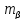 =5″
=5″
n=10
Решение:
Т.к
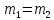 =
=
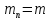 ,
используется формула:
,
используется формула:
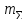 =
=
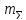 =5″
=5″ =15,8″
=15,8″
Ответ: 15,8″
