1.7. Принцип Даламбера для мт
Наряду
с рассмотренными методами изучения
движения МТ для решения задач динамики
несвободной МТ применяется метод
кинетостатики. Особенно удобен этот
метод в тех случаях, когда требуется
определить пассивную силу –реакцию
связи
при заданных активных силах
.
Запишем уравнение (1.2) для несвободной
МТ:
.
Перепишем это уравнение в виде:
.
(1.47)
Отсюда
следует, что вектор
можно рассматривать как некоторую силу,
которая, будучи приложенной к МТ,
уравновешивает активную и пассивную
силу – силу реакции наложенной на МТ
связи.
Эта сила называется силой инерции. Она равна по модулю произведению массы МТ на величину ее ускорения и направлена противоположно ускорению МТ:
.
(1.48)
С учетом обозначения (1.48) выражение (1.47) примет вид:
. (1.49)
Выражение (1.49) представляет собой принцип Даламбера для несвободной МТ.
Принцип Даламбера: Действующие на движущуюся МТ активные силы и пассивные силы – силы реакции связей можно в любой момент времени уравновесить добавлением к ним силы инерции (рис. 15).
Рис. 15
Следует
иметь в виду, что к МТ приложены только
силы
и
.
Сила же инерции к МТ не приложена, она
лишь условно прилагается к этой МТ.
Поэтому на уравнение (1.49) нельзя смотреть
как на условие равновесия активной
силы, пассивной силы – силы реакции
связи и силы инерции.
В случае прямолинейного движения МТ (рис. 16)
,
.
Рис. 16
В случае криволинейного движения МТ (рис. 17) сила инерции определяется по формуле:
,
где
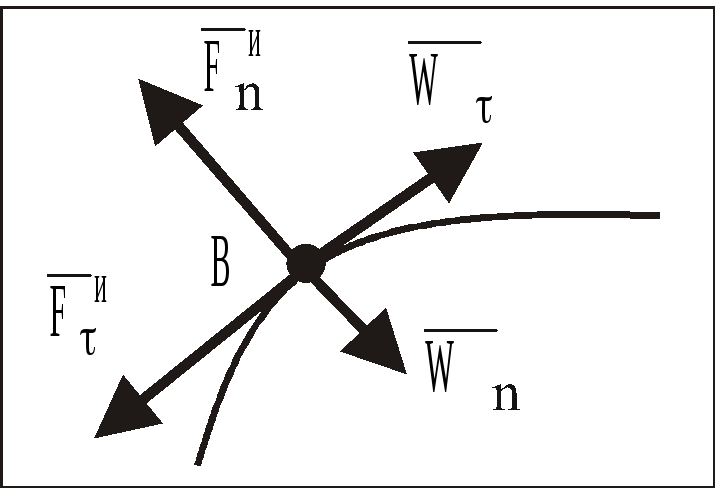
Рис. 17
Принцип Даламбера дает возможность при решении задач динамики составлять уравнение движения МТ в форме уравнений равновесия, используя для этого соответствующие уравнения или принципы статики. Эффективность такого метода особенно выявляется в динамике СМТ. В главе 5 будет дан алгоритм решения задач с помощью принципа Даламбера и примеры его использования , как для МТ, так и для СМТ.