Методические указания к выполнению задания 1 и 2

Центрально сжатые стержни, являющиеся элементами машиностоительных конструкций, рассчитываются на устойчивость по требуемому (заданному, допускаемому) коэффициенту запаса устойчивости [K_y] .

Условия устойчивости имеет вид

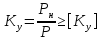
Здесь K_y – действительный коэффициент запаса устойчивости стержня.

Р_н – критическая сила, вычисляемая по формуле Л.Эйлера или по формуле Ф.С. Ясинского (в зависимости от максимальной гибкости стержня λ_max).

Р - сила, сжимающая стержень.

Величина [K_y] зависит от назначения и материала стержня. Например, для ходовых и грузовых винтов 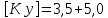, для чугунных стержней 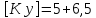, для деревянных стоек.

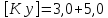Если потеря устойчивости стержня происходит при напряжениях меньше предела пропорциональности σ_п ,то критическая сила Р_к определяется по формуле Эйлера

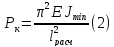
Где Е – модуль продольной упругости материала стержня.

Напряжение в поперечном сечении стержня при критическом значении сжимающей силы называются критическими

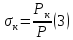
Формула Эйлера применима лишь при условии σ_к≤σ_п или, что то же самое ,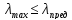

Наибольшая гибкость стержня вычисляется по формуле

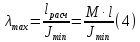
Где - 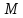- коэффициент приведения длины (коэффициент заделки); его велечина зависит от типа и расположения опор, а так же от характера нагрузки;

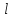– геометрическая длина стержня;

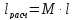- расчетная (приведенная) длина стержня;

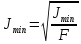- поперечный радиус инерции поперечного сечения (обычно минимальный);

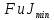- площадь и минимальный центральный момент инерции сечения стержня.

Предельная гибкость стержня (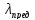) , при которой еще применима формула Эйлера , зависит только от физико-механических свойств материала и определяется по формуле

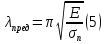
При ,критическая сила для стальных, дюралюминиевых и деревянных стержней определяется по линейной эмпирической формуле Ясинского

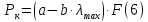
Где a и b – коэффициенты, зависящие от материала, определяются экспериментально и даны в литературе, имеют размерность напряжения.

Стержни малой гибкости (при 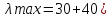рассчитывают не на устойчивость, а на прочность.

По условию устойчивости (1) можно выполнять расчеты трех типов:

1. Проверка устойчивости;

2. Определение наибольшей допустимости грузоподъемности;

3. Подбор сечения.

В задании 1 требуется выполнить два первых расчета. Рекомендуется следующая последовательность расчетных типов.

В задании 2 требуется подобрать необходимые размеры поперечного сечения сжатого стрежня. Методические указания даны в примере 2 . Студентам рекомендуется самостоятельно составить схему расчетов , аналогичную приведенной на с.4.

Пример 1. Стельной стержень постоянного сечения сжат силой Р = 60кН (рис. 1).

Требуется:

1. Проверить стержень на устойчивость, применяя формулу Эйлера или формулу Ясинского ( в зависимости от гибкости стержня), если требуется коэффициент запаса устойчивости [K_y] = 2,5, материал – сталь марки Ст.2 (Предел пропорциональности 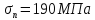, допускаемое напряжение на сжатие [σ_с] = 140 Мпа).

2. Определить наибольшее допустимое значение сжимающей силы [P] ,при заданной величине [K_y]. Сравнит напряжения: действительное σ, критическое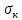, допускаемое на устойчивость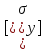и допускаемое при сжатии (без учета опасности продольного изгиба)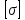

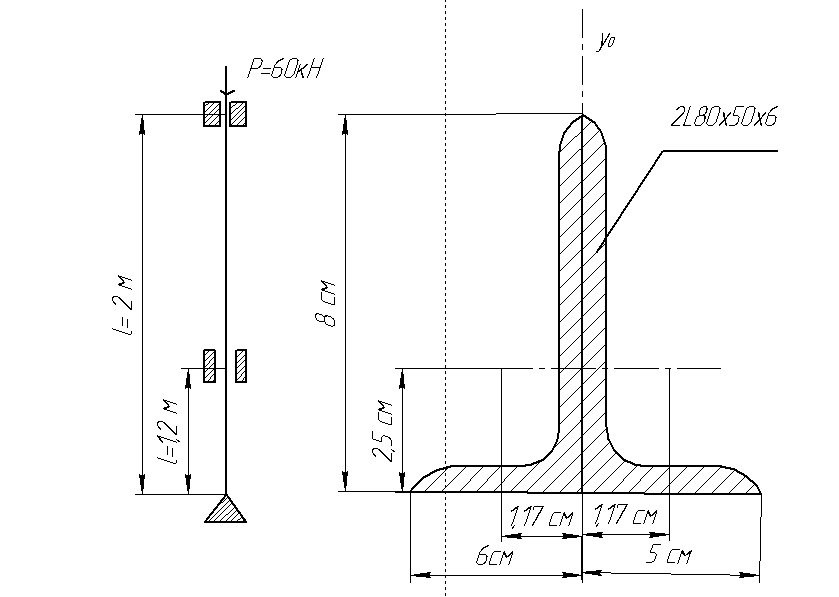
Рис. 1.

Решение

1. Геометрические характеристики поперечного сечения.

Сечения составляют из двух уголков 80х50х6 (ГОСТ 8510-57). Оси Х₀ и У₀ – главыне цетральные оси. Площадь сечения 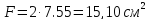. Шлавные центральные моменты инерции

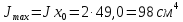
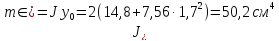
Минимальный радиус инерции

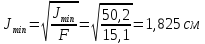
2. Проверка устойчивости стержня.

Условие устойчивости (1) при заданном значении имеет вид:

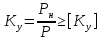
Максимальная гибкость стержня

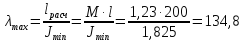
Для стали марки Ст.2 предельная гибкость равна 105:

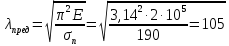
Так как 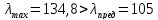, то для определения критической силы Р_к следует воспользоваться формулой Эйлера (2).

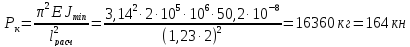
Коэффициент запаса устойчивости стержня

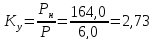
Стержень обладает достаточным устойчивости, так как

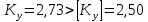
3. Наибольшая допустимая нагрузка при [K_y] =2,5.

Из условия устойчивости (1) следует

4. Сравнение напряжений.

Действительное нормальное напряжение в поперечном сечении стержня

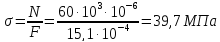
Критическое напряжение

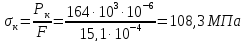
Допускаемое напряжение на устойчивость

Допускаемое напряжение при сжатии(без учета опасности продольного изгиба) [σ]= 140 МПа.

Имеем