
- •Анализ существующих методов построения связных передатчиков.
- •Анализ методов построения передатчиков с одной боковой полосой.
- •Обоснование технических требований.
- •Выбор структурной и расчет функциональной схемы
- •Выбор структурной схемы.
- •Расчет функциональной схемы.
- •Проектирование полосового lc – фильтра.
- •Расчет выходного каскада.
- •Выбор схемы.
- •Расчет электронного режима оконечного каскада
- •Расчет электронного режима предоконечного каскада
- •Расчет задающего генератора
- •Исходные данные
- •Расчет транзисторного автогенератора
- •Расчет цепей согласования
- •Расчет кпд передатчика
- •Заключение
- •Список литературы
-
Проектирование полосового lc – фильтра.
Перед началом расчета четко сформулируем требования к фильтру.
Верхняя
частота среза – 20503400 Гц (
 ).
).
Нижняя
частота среза – 20500300 Гц ( ).
).
Полоса
пропускания – 3100 Гц ( ).
).
Нормированная
частота -
 .
.
Гарантированное
затухание в полосе задерживания – 45 дБ
 .
.
Примем:
неравномерность затухания в полосе
пропускания – 0,177 дБ ( ).
).
Методика, по которой мы будем рассчитывать фильтр, приведена в [3], и основана на использовании таблиц значений элементов, нормированных по частоте и сопротивлению нагрузки. Определимся с выбором типа фильтра. Известны фильтры Баттерворта, Гаусса, Чебышева, Кауэра и т.д. Однако, в качестве полосовых фильтров используются только фильтры Чебышева и Кауэра, т. к. в процессе преобразования в полосовой фильтр остальные типы теряют линейность фазовых характеристик.
Выберем для построения фильтр Кауэра, т.к. для него необходим выбор гарантированного затухания в полосе задерживания, что облегчает расчет по требуемым данным.

Рис. 3.1. Частотные характеристики затухания фильтра Кауэра.
Каждый абзац должен быть отформатирован по границе справа. Исправить по всей записке.
По таблицам, приведенным в [3], ищем, сколько звеньев должен содержать фильтр Кауэра, удовлетворяющий нашим требованиям. Находим, n = 7. Таким образом, мы должны построить фильтр Кауэра 7 – го порядка.
Полосовой фильтр (ПФ) можно получить из ФНЧ прототипа. Построим ФНЧ фильтр Кауэра 7 – го порядка по схеме, изображенной на рис. 3.2.

Рис. 3.2. ФНЧ фильтр Кауэра 7-го порядка.
Чтобы из него получить требуемый ПФ, выполняют следующие преобразования, указанные на рис.3.3. После замены элементов ФНЧ прототипа, получим нужный полосовой фильтр Кауэра.

Рис. 3.3.Название.
В результате преобразований получаем вид ПФ Кауэра 7 – го порядка:

Рис. 3.4.?
Теперь найдем среднюю геометрическую частоту:

Нумерация формул?
Найдем
нормированные коэффициенты. На практике
обычно величины элементов фильтра
нормируются для частоты среза 1 рад/с и
при сопротивлении нагрузки 1 Ом. Для
преобразования нормированных величин
в реальные их необходимо умножить на
нормированные коэффициенты. Нормированные
индуктивность и емкость умножаются на
нормированные коэффициенты
 и
и
 ,
которые можно вычислить с помощью
формул:
,
которые можно вычислить с помощью
формул:


Примем сопротивление нагрузки R равным 100 Ом. Тогда:

 Коэффициент
преобразования ширины полосы:
Коэффициент
преобразования ширины полосы:

В таблице 3.1. приведены нормированные значения элементов из [3], для фильтра C07 – 20 – 62.
Таблица 3.1.
|
|
|
|
|
|
|
|
|
46,2 |
1,163 |
0,2125 |
0,177 |
1,9989 |
1,463 |
1,129 |
|
|
|
|
|
|
|
|
|
0,6748 |
1,1455 |
1,218 |
0,7925 |
0,7602 |
1,2883 |
0,7976 |
Из
таблицы находим
 .
Вычислим полосы пропускания режекторных
контуров 2, 4 и 6:
.
Вычислим полосы пропускания режекторных
контуров 2, 4 и 6:



Теперь найдем резонансные частоты для режекторных контуров 2, 4 и 6:
 -
резонансная частота для
-
резонансная частота для
 -
-
 .
.
 -
резонансная частота для
-
резонансная частота для
 -
-
 .
.
 -
для
-
для
 -
-
 .
.
 -
для
-
для
 -
-
 .
.
 -
для
-
для
 -
-
 .
.
 -
для
-
для
 -
-
 .
.
Рассчитаем дополнительные коэффициенты:



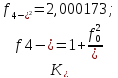


Из-за высокой частоты все дополнительные коэффициенты приблизительно равны. Теперь приступим к вычислению значений элементов полосового фильтра, показанного на рис. В скобках будем указывать номиналы реальных элементов.
-
Параллельный контур
 :
:

 ;
;


-
Режекторный контур 2:








-
Параллельный контур
 :
:




-
Режекторный контур 4:
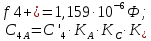







-
Параллельный контур
 :
:




-
Режекторный контур 6:






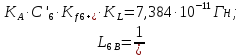

-
Параллельный контур
 :
:





 дБ
дБ











