
Раздел 2.9
Задача 2.1 Найти пределы
Вариант 4.
А)

Б)

В)

Г) x+6
x+6
А)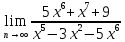
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Б) =
= =
= =
=
Применяя
частное правило пишу:
 как
как :
:
 это
непрерывная 4х, так
это
непрерывная 4х, так
 =
= = 3
= 3

 это
непрерывная 4х, так
это
непрерывная 4х, так
 =
= = 1
= 1
 =
-
=
-

Ответ:
-

В)

Найдём
след. пределы

Используем
tan
(2x2)
=
 , запишем
, запишем
 как
как :
:


Поскольку косинус – это непрерывная функция то:
 (2x2)
= cos (2 * 02)
= 1:
(2x2)
= cos (2 * 02)
= 1:

Используя капитальную формулу получаю:
 =
=
 =
=
 =
= =
=
По правилу
 =
=
 (
( )
(
)
( )
:
)
:



Применяя частное правило, запишу:
 как
как
 :
:
Поскольку косинус – это непрерывная функция то:
 cos
(5x) = cos(5 0) = 1
cos
(5x) = cos(5 0) = 1
 /1
/1
Поскольку косинус – это непрерывная функция то:
 cos
(2x2)
= cos(2 02)
= 1
cos
(2x2)
= cos(2 02)
= 1

Применяя частное правило, получаю:
 =
=
 =
=

Константа:

Применяя частное правило запишу:
 как
как
 :
:
Поскольку косинус – это непрерывная функция то:
 cos(5x)
= cos(5 0) = 1
cos(5x)
= cos(5 0) = 1
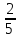 *1*
*1* =
= *1*
*1* =
=
Ответ:

Г) x+6
x+6
(x+3)x+6
(x+5)-x-6
=

Ответ:
![]()
Задача 2.2
Найти
производную
 если функция y(x)
задаётся так:
если функция y(x)
задаётся так:
А)
y=
Б) y=(1+tgx)x3
В) y*ex – x * ey + x2 – y =0
Г)

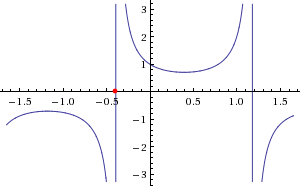
![]()
Б)
![]()

В)
![]()
Возможное
происхождение:![]()
Дифференциирую сумму почленно и выношу константы за скобки:
y (ex)
– ey
(ex)
– ey
 (x)
+
(x)
+ (x2)
+
(x2)
+
 (-y)
=
(-y)
= (0)
(0)
Производная для ex это ex:
-
(ey( +
+ (x2)
+
(x2)
+
 (-y)
+ exy
=
(-y)
+ exy
=
 (0)
(0)
Производная из x это 1
exy
+
 (x2)
+
(x2)
+
 (y)
-1ey
=
(y)
-1ey
=
 (0)
(0)
Используем
формулу силы:
 (xn)
= nxn-1,
так n
= 2/
(xn)
= nxn-1,
так n
= 2/ (x2)
= 2x:
(x2)
= 2x:
-ey
+
exy
+
 (-y)
+2x =
(-y)
+2x =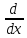 (0)
(0)
Производная из y это 0:
-ey
+ 2x
+ exy
+ 0 =
 (0)
(0)
Упрощаю выражение:
-ey
+ 2x
+ exy
=
 (0)
(0)
Производная из 0 это 0:
Ответ: -ey + 2x + exy = 0
Г)
Решение:
Функция задана в параметрическом виде. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.
yx
=

Отдельно нахожу производные xt' и yt' xt' = -5t•sin(5t) + cos(5t)
yt'
= (t+1)(6tg(6t)2+6)+tg(6t)
Следовательно:
![]() или
или![]()
Контрольная работа №3
Раздел 2.9
Задача
2.4 Провести полное исследование функции
и построить график функции y
=

Решение:
1) Область определения функции:
x € (-∞,0) (0,∞)
2) Пересечение с ось абсцисс (ox)
y
=
 = 0 ↔ Действительных решений нет
= 0 ↔ Действительных решений нет
3) Поведение функции в граничных точках области определения:
x
= 0,
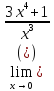 не существует
не существует
x=
0,
 = -∞
= -∞
x=0,
 = ∞
= ∞
4) Поведение функции на бесконечности
 =
∞
=
∞
 =
-∞
=
-∞
5) Наклонная асимптота функции:
y = 3x
6) Исследование функции на чётность\нечётность:
f(x)
=
 f(-x)
=
f(-x)
=

Функция является нечётной
7) Производная функции равна:
12-

8) Нули производной:
x = -1
x = 1
9)
Функция возрастает на: x
€ (-∞, -1 ![]()
10)
Функция убывает на:![]()
11) Минимальное значение функции: - ∞
12) Максимальное значение функции: ∞
13)Интервалы выпуклости и вогнутости функции:
f''(x)
= -36/x+12(3x4+1) / x5 или

Нахожу корни уравнения. Для этого полученную функцию приравниваю к нулю.

Для данного уравнения корней нет
|
(-∞ ;0) |
(0; +∞) |
|
f''(x) < 0 |
f''(x) > 0 |
|
функция выпукла |
функция вогнута |
Построение графика функции:

Задача 2.6 Найти частные производные первого порядка d(xy)
Вариант 4: z = x + sin(xy) + y – cos(yx)
Частная производная первого порядка по х:
 (x+sin(xy)-cos(yx)
= y sin(xy)+y cos(xy)+1
(x+sin(xy)-cos(yx)
= y sin(xy)+y cos(xy)+1
Частная производная первого порядка по y:
 (x+sin(xy)-cos(yx)
=x(sin(xy)+cos(xy))
(x+sin(xy)-cos(yx)
=x(sin(xy)+cos(xy))

Задача 2.9 Найти неопределённые интегралы. Вариант 4:
А)
∫(4 + 8x4)
(x+5
+ 8x4)
(x+5 -2x)
dx;
-2x)
dx;
Б)
∫ dx;
dx;
B) ∫ln (2x+4) dx
А)
∫ (4 + 8x4)
(x+5
+ 8x4)
(x+5 -2x)
dx
=
-2x)
dx
=
 -
- -
- -
-
Возьму интеграл:
∫ (5 -x)
(8x
+ 4
-x)
(8x
+ 4 )dx
)dx
Для
подынтегрального выражения (5 -x)
(8x
+ 4
-x)
(8x
+ 4 )
заменюu
=
)
заменюu
= иdu
=
иdu
=
 dx
= 2∫-4u(42-5u)
(2u8+
dx
= 2∫-4u(42-5u)
(2u8+ )du
)du
Фактор констант:
-8∫u(42-5u)
(2u8+ )du
)du
Расширение
подынтегрального выражения 4u(42-5u)
(2u8+ )
даёт 2u11-10u10-5(u2)6/5+u3
)
даёт 2u11-10u10-5(u2)6/5+u3 :
:
=
-8∫(2u11-10u10-5(u2)6/5+u3 u3)
du
u3)
du
Объединить сумму почленно и вынести константы за скобки:
40
∫ (u2)6/5du-8
∫ u3 du-16
∫ u11du+80
∫u10du
du-16
∫ u11du+80
∫u10du
Для подынтегрального выражения (u2)6/5 упростить полномочия
40
∫ u12/5du-8
∫ u3 du-16
∫ u11du+80
∫u10du
du-16
∫ u11du+80
∫u10du
Интеграл
из u12/5
это

 –8∫
u3
–8∫
u3 du-16
∫ u11du+80
∫u10du
du-16
∫ u11du+80
∫u10du
Для
подынтегрального выражения u3 заменю s=u2
и ds=2u
du
заменю s=u2
и ds=2u
du
 –4∫
s6/5ds-16
∫ u11du+80
∫u10du
–4∫
s6/5ds-16
∫ u11du+80
∫u10du
Интеграл
из s6/5
это

 +
+
 -16 ∫u11du+80
∫u10du
-16 ∫u11du+80
∫u10du
Интеграл
из u11
это

 +
+
 -
- + 80 ∫u10du
+ 80 ∫u10du
Интеграл
из u10
это

 +
+
 -
- +
+
Займу назад с s = u2:
 -
-
 +
+ -
- (u2)11/5
(u2)11/5
Займу назад с u = √x
Ответ:
 +
+
 -
- +
+
Б)
∫ dx
dx
Вынесу константу за скобки:
 ∫
∫ dx
dx
Для
подынтегрального выражения
 заменюu=ln(3x)
и du=
заменюu=ln(3x)
и du=
 dx
dx
=
 ∫u
dx
∫u
dx
Интеграл
из u
это
 =
=
Заменю
назад для u
= ln(3x)
=
 ln2(3x)
ln2(3x)
B) ∫ln (2x+4) dx
Для
подынтегрального выражения ln(2x+4)
заменю u
= 2x+4
и du
= 2dx:
 ∫ln(u)du
∫ln(u)du
Для
подынтегрального выражения, объеденённые
частями ∫f
dg=fg
- ∫gdf,
откуда f
= ln(u),
dg
= du,
df
= du,
g
= u
du,
g
= u
 u
ln(u)
-
u
ln(u)
-
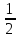 ∫1du
∫1du
Интеграл из 1 это u:
 u
ln(u)
-
u
ln(u)
-

Заменю назад для u = 2x+4
= -x+(x+2) ln(2(x+2)) -2
Фактический ответ выглядит:
(x+2) (ln(2(x+2)) -1)
Ответ: (x+2) ln(2(x+2)) – x
Задача 2.10 Найти плоскую меру множества, ограниченного заданными линиями на плоскости Оxy, сделать чертёж
Вариант 4: y2 = 3+2x y=x
1) Нахожу точки пересечения двух линий: y = (-1; 3)
2) Построю фигуру на плоскости Oxy, ограниченную y2 = 3+2x - параболой и y = x – прямой.

Нахожу площадь фигуры:
Вычисляю первообразную (интеграл) для функции (константу, возникающую при интегрировании, здесь не учитываем):
F(y)
= =
= dy =
dy = +
+ -
-
В итоге получил:
F(y)= +
+ -
-
По теореме Ньютона-Лейбница определенный интеграл можно представить как:
 =
F(y)
=
F(y)
Подставляю в данную формулу данные, а именно первообразную и пределы интегрирования:
 =
(
=
( +
+ -
- )
) (
( +
+ -
- )
- (
)
- ( +
+ -
- )
=
)
=
=
 – (-
– (- ) =
) = = 5.33
= 5.33
Ответ: S фигуры = 5.33
