
Контрольная работа №1 по математике Студента 1 курса сгуГиТ
Раздел 1.5
Задача 1.1
Заданы матрицы А,В,С. Найти: а)(3А + 2В) С; в)вычислить определитель матрицы А
Решение: а)
|
3 |
· |
A |
+ |
2 |
· |
B |
= |
3 |
· |
|
+ |
2 |
· |
|
= | ||||||||||||||||||||||
|
= |
|
3·(-4) + 2·1 |
3·(-2) + 2·(-1) |
3·(-3) + 2·(-2) |
|
= |
|
3·2 + 2·(-2) |
3·4 + 2·1 |
3·0 + 2·(-2) | ||||
|
3·(-1) + 2·(-1) |
3·(-4) + 2·2 |
3·(-3) + 2·3 |
|
|
|
-10 |
-8 |
-13 |
| |||||
|
|
2 |
14 |
-4 |
| ||||||
|
|
-5 |
-8 |
-3 |
| ||||||
|
= |
|
· |
|
= | ||||||||||||||||||||||
|
|
|
-3 |
9 |
28 |
| |||||
|
|
70 |
18 |
58 |
| ||||||
|
|
-28 |
-6 |
-12 |
| ||||||
в) Вычислить определитель матрицы А
|
А= |
|
| ||||||||||||||||||||||||
|
= |
(-4) |
· |
|
- |
(-2) |
· |
|
+ |
(-3) |
· |
|
=48 | ||||||||||||||
Задача 1.2
Для матрицы А найти: а) A-1; б) АA-1; в) решить систему Аx = В.
|
|
-15 |
|
|
|
3 |
| ||
|
-25 |
|
Дано: А b
|
|
|
4 |
-1 |
1 |
|
|
|
4 |
1 |
4 | ||
|
|
2 |
-3 |
-2 |
Решение:
Найдем обратную матрицу с помощью элементарных преобразований, для этого припишем справа единичную матрицу такого же размера:
|
|
4 |
-1 |
1 |
1 |
0 |
0 |
|
|
4 |
1 |
4 |
0 |
1 |
0 | ||
|
2 |
-3 |
-2 |
0 |
0 |
1 |
Строку 1 делим на 4:
|
|
1 |
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
4 |
1 |
4 |
0 |
1 |
0 | ||
|
2 |
-3 |
-2 |
0 |
0 |
1 |
Вычитаем из строки 2 строку 1, умноженную на 4:
|
|
1 |
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
2 |
3 |
-1 |
1 |
0 | ||
|
0 |
-3 |
-2 |
0 |
0 |
1 |
Вычитаем из строки 3 строку 2, умноженную на 2:
|
|
1 |
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
2 |
3 |
-1 |
1 |
0 | ||
|
0 |
-2.5 |
-2.5 |
-0.5 |
0 |
1 |
Строку 2 делим на 2:
|
|
1 |
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
1 |
1.5 |
-0.5 |
0.5 |
0 | ||
|
0 |
-2.5 |
-2.5 |
-0.5 |
0 |
1 |
Вычитаем из строки 3 строку 2, умноженную на -2.5:
|
|
1 |
|
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
|
1 |
1.5 |
-0.5 |
0.5 |
0 | ||
|
0 |
|
0 |
1.25 |
-1.75 |
1.25 |
1 |
Строку 3 делим на 1.25:
|
|
1 |
-0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
1 |
1.5 |
-0.5 |
0.5 |
0 | ||
|
0 |
0 |
1 |
-1.4 |
1 |
0.8 |
Вычитаем из строки 2 строку 3, умноженную на 1.5
|
|
1 |
|
0.25 |
0.25 |
0.25 |
0 |
0 |
|
|
0 |
|
1 |
0 |
1.6 |
-1 |
-1.2 | ||
|
0 |
|
0 |
1 |
-1.4 |
1 |
0.8 |
Вычитаем из строки 1 строку 3, умноженную на 0.25:
|
|
1 |
|
0.25 |
0 |
0.6 |
-0.25 |
-0.2 |
|
|
0 |
|
1 |
0 |
1.6 |
-1 |
-1.2 | ||
|
0 |
|
0 |
1 |
-1.4 |
1 |
0.8 |
Вычитаем из строки 1 строку 2, умноженную на - 0.25:
|
|
1 |
|
0 |
0 |
1 |
-0.5 |
-0.5 |
|
|
0 |
|
1 |
0 |
1.6 |
-1 |
-1.2 | ||
|
0 |
|
0 |
1 |
-1.4 |
1 |
0.8 |
|
А-1 = |
|
1 |
-0.5 |
-0.5 |
|
|
1.6 |
-1 |
-1.2 | |||
|
-1.4 |
1 |
0.8 |
Проверю правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.
Находим АА-1:
|
|
4 |
-1 |
1 |
|
|
4 |
1 |
4 | ||
|
2 |
-3 |
-2 |
|
|
10 |
-5 |
-5 |
| ||||
|
16 |
-10 |
-12 |
| |||||
|
-14 |
10 |
8 |
| |||||
|
|
(4•10)+(-1•16)+(1•(-14)) |
|
|
|
|
(4•(-5))+(-1•(-10))+(1•10) |
|
|
|
|
|
(4•(-5))+(-1•(-12))+(1•8) |
|
|
(4•10)+(1•16)+(4•(-14)) |
|
|
|
|
(4•(-5))+(1•(-10))+(4•10) |
|
|
|
|
|
(4•(-5))+(1•(-12))+(4•8) | ||
|
(2•10)+(-3•16)+(-2•(-14)) |
|
|
|
|
(2•(-5))+(-3•(-10))+(-2•10) |
|
|
|
|
|
(2•(-5))+(-3•(-12))+(-2•8) |
|
АА-1 = |
|
1 |
0 |
0 |
|
|
0 |
1 |
0 | |||
|
0 |
0 |
1 |
|
А-1 = |
|
1 |
-0.5 |
-0.5 |
|
|
1.6 |
-1 |
-1.2 | |||
|
-1.4 |
1 |
0.8 |
Находим Аx = В
Так как обратная матрица равняется:
|
|
-15 |
|
|
|
3 |
| ||
|
-25 |
|
|
|
|
|
|
1(-15)+(-0,5)*3+(-0,5)(-25) |
|
| ||||||
|
|
|
|
16(-15)+(-1)*3+1,2(-25) |
|
| |||||||
|
|
|
|
(-1,4)(-15)+1*3+0,8(-25) |
|
| |||||||
|
|
-2 |
|
| |||
|
-273 |
|
| ||||
|
4 |
|
| ||||
|
|
1 |
-0.5 |
-0.5 |
|
|
4 |
-1 |
-1.2 | ||
|
-1.4 |
1 |
0.8 |
Задача 1.3
Решить систему уравнений методом Гаусса
Исходная система уравнений имеет вид:
2x - 3y + 5z= -34
-3x - 2y + 5z= -18
x - 2y + 2z= -15
Решение:
Найду определитель главной матрицы, составленной из коэффициентов при X1 - n:
|
= -81 |
|
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Достоим главный определитель системы уравнений еще одним столбцом, в который вставлю значения за знаком равенства.
|
|
|
|
Теперь последовательно, при помощи элементарных преобразований преобразую левую часть матрицы (3 × 3) до треугольного вида (обнулю все коэффициенты находящиеся не на главной диагонали, а коэффициенты на главной диагонали преобразую до единиц).
Вычитаю 1-ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
|
Вычитаю 2-ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
|
Вычитаю 3-ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
|
Вычту 2-ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
|
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
|
|
|
|
Числа получившиеся правее единичной матрицы и будут решением системы
уравнений.
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
2·(-3) - 3·1 + 5·(-5) = -6 - 3 - 25 = -34
-3·(-3) - 2·1 + 5·(-5) = 9 - 2 - 25 = -18
(-3) - 2·1 + 2·(-5) = -3 - 2 - 10 = -15
x = -3
y =1
z = -5
Задача 1.4
Использовать совместность каждой системы A и B, для совместной системы найти решение.
Дано:
A B
6y – 3z = 3 -x + 2y + 4z = 1
-3x – 3y + 3z = 2 -3x + 2y = -1
3x + y – 2z = 10 -5x + 6y + 8z = 1
Решение:
А) Перепишем систему уравнений в матричном виде и решим его методом Гаусса
|
|
0 |
6 |
-3 |
3 |
|
|
-3 |
-3 |
3 |
2 | ||
|
3 |
1 |
-2 |
10 |
поменяем 1-ую строку и 2-ую строку местами
|
|
-3 |
-3 |
3 |
2 |
|
|
0 |
6 |
-3 |
3 | ||
|
3 |
1 |
-2 |
10 |
1-ую строку делим на -3
|
|
1 |
1 |
-1 |
-2/3 |
|
|
0 |
6 |
-3 |
3 | ||
|
3 |
1 |
-2 |
10 |
от 3 строк отнимаем 1 строку, умноженную соответственно на 3
|
|
1 |
1 |
-1 |
-2/3 |
|
|
0 |
6 |
-3 |
3 | ||
|
0 |
-2 |
1 |
12 |
2-ую строку делим на 6
|
|
1 |
1 |
-1 |
-2/3 |
|
|
0 |
1 |
-0.5 |
0.5 | ||
|
0 |
-2 |
1 |
12 |
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на 1; -2
|
|
1 |
0 |
-0.5 |
-7/6 |
|
|
0 |
1 |
-0.5 |
0.5 | ||
|
0 |
0 |
0 |
13 |
Ответ: Система уравнений не имеет решений так как: 0 ≠ 13
Исследуем систему на совместность.
rank
|
|
0 |
6 |
-3 |
|
|
-3 |
-3 |
3 | ||
|
3 |
1 |
-2 |
=2 rank
|
|
0 |
6 |
-3 |
3 |
|
|
-3 |
-3 |
3 |
2 | ||
|
3 |
1 |
-2 |
10 |
=3 Ранг расширенной матрицы системы не равен рангу матрицы системы => система несовместна (не имеет решений).
B) Перепишем систему уравнений в матричном виде и решим его методом Гаусса
|
|
-1 |
2 |
4 |
1 |
|
|
-3 |
2 |
0 |
-1 | ||
|
-5 |
6 |
8 |
1 |
1-ую строку делим на -1
|
|
1 |
-2 |
-4 |
-1 |
|
|
-3 |
2 |
0 |
-1 | ||
|
-5 |
6 |
8 |
1 |
от 2; 3 строк отнимаем 1 строку, умноженную соответственно на -3; -5
|
|
1 |
-2 |
-4 |
-1 |
|
|
0 |
-4 |
-12 |
-4 | ||
|
0 |
-4 |
-12 |
-4 |
2-ую строку делим на -4
|
|
1 |
-2 |
-4 |
-1 |
|
|
0 |
1 |
3 |
1 | ||
|
0 |
-4 |
-12 |
-4 |
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на -2; -4
|
|
1 |
0 |
2 |
1 |
|
|
0 |
1 |
3 |
1 | ||
|
0 |
0 |
0 |
0 |
Ответ:
|
|
x + 2z = 1 |
|
y + 3z = 1 |
Исследуем систему на совместность.
Rang A = 2
|
|
-1 |
2 |
4 |
|
|
-3 |
2 |
0 | ||
|
-5 |
6 |
8 |
rang B = 2
|
|
-1 |
2 |
4 |
1 |
|
|
-3 |
2 |
0 |
-1 | ||
|
-5 |
6 |
8 |
1 |
Ранг расширенной матрицы равен рангу матрицы системы, но меньше числа неизвестных => система совместна и имеет бесконечно много решений.
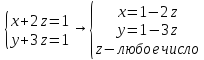 –бесконечное
множество решений
–бесконечное
множество решений
Задача 1.5
Даны вершины пирамиды A(x1,y1,z1), B(x2,y2,z2), C(x3,y3,z3), D(x4,y4,z4). Найти: а) угол между векторами СА и СВ; б) площадь грани АВС; с) проекцию вектора СА на вектор СD; г) объём пирамиды; д) длину высоты пирамиды, опущенной из вершины D.
А) Координаты векторов находим по формуле: X = x2 – x1; Y = y2 – y1; Z = z2 – z1 здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Для вектора СА a X = x2 - x1; Y = y2 - y1; Z = z2 - z1 X = 7-5; Y = 2-3; Z = 2-1
Для вектора СВ b - X = 5-5; Y = 7-3; Z = 7-1
Решение:Найти угол между векторами a = {2; -1; 1} и b = {0; 4; 6}.
Найдем скалярное произведение векторов:
a * b= 2 · 0 + (-1) · 4 + 1 · 6 = 0 + (-4) + 6 = 2.
Найдем модули векторов:
a = √22 + (-1)2 + 12 = √4+1+1 = √6 = 2.4 b = √02 + 42 + 62 = √0 + 16 + 36= √52 = 7.2
Найдем угол между векторами:
|
cos α = |
a * b |
= |
2 |
= |
2 |
|
a * b |
2.4 · 7.2 |
17.28 |
Ответ: угол векторов СА и СВ = 83.6°
Б) Площадь грани АВС может быть найдена как половина площади параллелограмма построенного на векторах АВ и АС. Площадь этого параллелограмма равна модулю векторного произведения векторов АВ и АС [AB{x1, y1, z1} ; AC(x2, y2, z2}]= {a1, a2, a3}, где a1, a2, a3 вычисляются по формулам: a1=y1*z2-y2*z1; a2=x1*z2-x2*z1; a3=x1*y2-y1*x2; Получаем: [AB ; AC]={-10, -12, 8} Вычислим длину: N = √-102+(-12)2 +82 = √100+144+64 = √308 Вынести из-под корня ничего нельзя, поэтому он войдёт в ответ в неизменном виде.
SABC
=
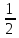 * N
=
* N
= = 8.7
= 8.7
Площадь грани АВС = 8.7 ед2
C) Проекция вектора СА на вектор СD
Решение:
|
CD CA = |
CA· CD |
|
|CD| |
Найдем скалярное произведение векторов:
CA * CD = CAx * CDx + CAy * CDy + CAz * CDz
|
CA · CD= |
2 |
· |
(-5) |
+ |
(-1) |
· |
1 |
+ |
1 |
· |
5 |
= |
-10 |
- |
1 |
+ |
5 |
= |
-6 |
Найдем модуль векторов: |CD| = √CDx2 + CDy2 + CDz2 = √(-5)2 + 12 + 52 = √25 + 1 + 25 = √51
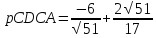 =
0.8
=
0.8
|
Ответ: Проекция вектора СА на вектор СD равна 0.8 |
|
Г) Объём пирамиды
Пирамида с вершинами:
|
А: |
( |
7 |
, |
2 |
, |
2 |
) |
|
В: |
( |
5 |
, |
7 |
, |
7 |
) |
|
С: |
( |
5 |
, |
3 |
, |
1 |
) |
|
D: |
( |
2 |
, |
3 |
, |
7 |
) |
Найдем координаты векторов, описывающих введенную пирамиду
(Поочереди вычтя из координат точки А соответствующие координаты остальных точек.)
|
Вектор № 1: |
( |
2 |
, |
-5 |
, |
-5 |
) |
|
Вектор № 2: |
( |
2 |
, |
-1 |
, |
1 |
) |
|
Вектор № 3: |
( |
5 |
, |
-1 |
, |
-5 |
) |
Получили матрицу:
|
|
|
|
Определитель данной матрицы равен:
Перемножим построчно:
(2) × (-1) × (-5) + (-5) × (1) × (5) + (-5) × (2) × (-1) - (-5) × (-1) × (5) - (-5) × (2) × (-5) - (2) × (1) × (-1) = 78
|
= 78 |
|
Ответ: Согласно описанному выше методу объем введенной Вами пирамиды равен = 78/6 = 13 (ед3)
Д) Найти длину высоты пирамиды, опущенной из вершины D.
Чтобы найти длину высоты, опущенной на грань АВС, надо использовать формулу объема пирамиды, известную из геометрии: V=1/3*Sосн*H
В этой формуле нам известны и объём и площадь соответствующей грани. Высота может быть расчитана по формуле: H=3V/Sосн
H = 3 * 13 / 8.7 = 4.44
Ответ: Высота, опущенная на грань ABC равна: 4.44
