
- •Лабораторное занятие № 4 Тема: Дифференциальное исчисление функций одной переменной
- •Ход занятия
- •Дифференцирование функций, заданных параметрически.
- •Геометрические и механические приложения производной
- •Исследование поведения функции
- •Интервалы монотонности и экстремум функции
- •Применение правила отыскания наибольших и наименьших значений функций при решении задач
- •Интервалы выпуклости функции. Точки перегиба
- •Асимптоты графика функции
- •Общая схема исследования функций:
- •3. Необходимо выполнить:
- •Практические задания общие по темам: "Понятие производной. Техника дифференцирования функций. Геометрические и механические приложения производной"
- •Вариант 1.
- •Индивидуальные задания по темам: "Теорема Лагранжа. Условия постоянства, возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум"
- •Практические задания общие
- •Индивидуальные задания по теме:
- •Практические задания общие
- •Индивидуальные задания по теме:
- •Практические задания общие
- •Индивидуальные задания по теме: "Общая схема исследования функции и построения ее графика"
- •Литература Основная
- •Дополнительная
- •Интернет-ресурсы
Вариант 1.
1.
Найти производные
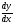 данных функций :
данных функций :
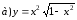

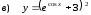
2.
Составить уравнение касательной и
нормали к кривой
 ,
в точке с абсциссой
,
в точке с абсциссой .
.
3.
Показать, что если тело движется по
закону

то его ускорение равно пройденному пути.
Вариант 2.
1.
Найти производные
 данных функций :
данных функций :



2.
Написать уравнение касательной и нормали
к кривой
 в точке с абсциссой
в точке с абсциссой
3.
Тело массой 100 кг движется прямолинейно
по закону

Определить кинетическую энергию тела через 5 сек. после начала движения.
Вариант 3.
1. Найти производные следующих функций:



2.
Составить уравнение касательной и
нормали к кривой
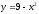 ,
в точке с абсциссой
,
в точке с абсциссой .
.
3.
Показать, что если тело движется по
закону
 то
его ускорение равно пройденному пути.
то
его ускорение равно пройденному пути.
Практические задания общие
по темам: "Теорема Лагранжа. Условия постоянства, возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум"(ОК-1, ОК-20, ОК-22):
Задание 1. На кривой y = 4 − 6x3, найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(−1, 10) и B(2, −44).
Угловой
коэффициент хорды, соединяющей точки
точки A
и B,
равен
 ,
а угловой коэффициент касательной к
кривойy = f(x)
в точке M
равен
,
а угловой коэффициент касательной к
кривойy = f(x)
в точке M
равен
 .
Отсюда
.
Отсюда .
Так как
.
Так как ,
тоx0 = 1.
Таким образом M = (1, f(1)) = (1, −2).
,
тоx0 = 1.
Таким образом M = (1, f(1)) = (1, −2).
Задание 2. Найти стационарные точки функции f(x) = xln x на промежутке X = (0; +∞).
Стационарной
точкой функции f(x)
на множестве X
называется внутренняя точка x0
множества X,
такая, что
 .
Найдем
.
Найдем .
. .
Точка
.
Точка —
внутренняя точка множестваX,
следовательно, она является стационарной
точкой функции f(x)
на множестве X.
—
внутренняя точка множестваX,
следовательно, она является стационарной
точкой функции f(x)
на множестве X.
Задание 3. Записать формулу Лагранжа для функции f(x) = x3 − 5 на отрезке [−1; 2] и найти соответствующее значение c.
Условия
теоремы Лагранжа для этой функции
выполняются,
 .
Тогда по теореме Лагранжа:
.
Тогда по теореме Лагранжа: .
Так как −1 (−1; 2),
то c = 1.
.
Так как −1 (−1; 2),
то c = 1.
Задание
4. Определить интервалы монотонности
функции
 .
.
Область определения
этой функции
 .
.

Найдем промежутки
знакопостоянства производной
 ,
решив неравенство
,
решив неравенство на области определения:
на области определения:


Следовательно,
промежутки возрастания функции f(x):
 и
и ,
промежутки убывания:
,
промежутки убывания: .
.
Задание
5. Определить интервалы монотонности
функции
 .
.
Область определения
этой функции
 .
.

Найдем промежутки
знакопостоянства производной
 ,
решив неравенство
,
решив неравенство на области определения:
на области определения:
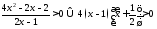

Следовательно,
функция f(x)
возрастает на промежутке:
 ,
а убывает на промежутке:
,
а убывает на промежутке: .
.
Индивидуальные задания по темам: "Теорема Лагранжа. Условия постоянства, возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум"
(ОК-1, ОК-20, ОК-22)
На кривой y = 6x3 + 7 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(−1, 1) и B(2, 55);
На кривой y = x2 − 2x + 12 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(0, 12) и B(1, 11
На кривой y = −4x2 + 9 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(0, 9) и B(1, 5);
На кривой y = 2x2 −3 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(1, −1) и B(3, 15);
На кривой y = x3 − x + 12 найти точки M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(−1, 12) и B(2, 18);
На кривой y = 2x3 − 8x + 5 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(-1, 11) и B(2, 5);
На кривой y = 5 – 3x3 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(-2, 29) и B(1, 2);
На кривой y = –2x2 + 5x – 3 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(0, –3) и B(1, 0);
Записать формулу Лагранжа для функции f(x) = 5x3 + 8 на отрезке [0; 1] и найти соответствующее значение c;
На кривой y = 6x2 − 4x – 2 найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки A(0, 2) и B(2, 14);
Записать формулу Лагранжа для функции f(x) = 4x2 + 2 на отрезке [0; 1] и найти соответствующее значение c;
Записать формулу Лагранжа для функции f(x) = 4x3 − 9 на отрезке [−1;0] и найти соответствующее значение c;
Записать формулу Лагранжа для функции f(x) = 11 − 7x3 на отрезке [−3; 0] и найти соответствующее значение c;
Записать формулу Лагранжа для функции f(x) = 6 − 5x3 на отрезке [−2; 1] и найти соответствующее значение c;
Записать формулу Лагранжа для функции f(x) = x4 − 2x + 1 на отрезке [−1; 0] и найти соответствующее значение c;
Найти стационарные точки функции f(x) = arctg x2 на промежутке X = (−1; 1);+0;
Найти стационарные точки функции
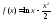 на промежуткеX = (0; 2);
на промежуткеX = (0; 2);
Найти стационарные точки функции
 на промежуткеX = (−∞; +∞);
на промежуткеX = (−∞; +∞);
Найти стационарные точки функции
 на промежуткеX = (−∞; +∞);
на промежуткеX = (−∞; +∞);Найти интервалы, на которых функция f(x) = x2e-x возрастает;
Найти интервалы, на которых функция f(x) = 3x - 3x2 + x3 убывает;
Найти интервалы, на которых функция
 возрастает;
возрастает;Найти интервалы, на которых функция
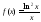 возрастает;
возрастает;Найти интервалы, на которых функция
 возрастает;
возрастает;Найти интервалы, на которых функция
 возрастает;
возрастает;Найти интервалы, на которых функция
 убывает;
убывает;Найти интервалы, на которых функция
 возрастает;
возрастает;Найти интервалы, на которых функция f(x) = x + ln(1 - 3x) убывает;
Найти интервалы, на которых функция
 убывает;
убывает;
