Интервалы монотонности и экстремум функции

1. Если производная функции у=f(х) положительна (отрицатель­на) во всех точках промежутка, то функция у=f(х) монотонно воз­растает (убывает) на этом промежутке.

2. Точка 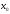называется точкой максимума (минимума) функции y = f(х), если существует интервал, содержащий точку, такой, что для всех х из этого интервала имеет место неравенство, (). Точки максимума и минимума называются точками экстремума.

3. Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю (f'(x) =0), либо не существует.

4. Первое достаточное условие экстремума: если в точке функ­ция у = f(х) непрерывна, а производная f'(x) при переходечерез точку меняет знак, то точка - точка экстремума: максимума, если знак меняется с «+» на «-», и минимума, если с «-» на «+».

Если при переходе через точку производная не меняет знак, то в точкеэкстремума нет.

5. Второе достаточное условие экстремума: если в точкеf'() = 0,a f"() > 0, то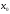является точкой минимума функции. Ес­лиf'() = 0, а f"()<О, тоявляется точкой максимума функции.

6. Схема исследования функции у = f(х) на экстремум:

1) найти производную у' = f'(x);

2) найти критические точки функции, в которых производная равна нулю или не существует;

3) исследовать знак производной слева и справа от каждой кри­тической точки и сделать вывод о наличии экстремумов функции;

4) найти экстремальные значения функции.

При исследовании функции на экстремум с помощью 2-го достаточно­го условия необходимо найти вторую производную f"(х) и определить ее знак в каждой критической точке.

Применение правила отыскания наибольших и наименьших значений функций при решении задач

При решении задач этой темы следует иметь в виду, что наибольшее и наименьшее значения функция достигает либо на концах заданного отрезка, либо в тех его внутренних точках, которые являются критическими точками первого рода этой функции (точками, подозрительными на экстремум).

1. Чтобы найти наибольшее и наименьшее значение функции у = f(х) на отрезке [а,b], следует выбрать наи­большее (наименьшее) из значений функции в критических точках, нахо­дящихся в интервале (а, b) и на концах отрезка (в точках а и b).

2. Если дифференцируемая на интервале (а, b) функция у = f(х) имеет единственную точку экстремума, то в этой точке достигается наибольшее или наименьшее значение функции на интервале (а, b).

Интервалы выпуклости функции. Точки перегиба

1. Функция у=f(х) называется выпуклой вверх (вниз) на проме­жутке, если для любых двух значений из этого промежутка вы­полняется неравенство:

Точки, разделяющие интервалы выпуклости, называются точками перегиба.

2. Если вторая производная f"(х) функции у=f(x) положительна (отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке.

3. Если - точка перегиба функции у =f(x) и f"() существует,

f"() = 0.

4. Если вторая производная f"(x) меняет знак при переходе через точку ,то точка является точкой перегиба функции у =f(х).

5. Схема исследования функции на выпуклость и точки перегиба:

1) найти вторую производную функции f"(x);

2) найти точки, в которых вторая производная f"(x) =0 или не существует;

3) исследовать знак второй производной слева и справа от най­денных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба;

4) найти значения функции в точках перегиба.