Задача 5.1.5

Точка совершает гармонические колебания, уравнение которых x=A·sinωt , где А =5 см, ω=2 с^-1. В момент времени, когда точка обладала потенциальной энергией равной 10^-4 Дж, на нее действовала возвращающая сила 5·10^-3Н. Найти этот момент времени и соответствующую ему фазу колебаний.

Дано: А = 5 см = 510^-2 м, ω = 2 с^-1, ,.

Решение:

Дифференцируя заданное уравнение колебаний, находим выражения для скорости и ускорения точки:

, (1)

. (2)

Если обозначит массу точки как m, то закон изменения возвращающей силы, с учётом (2), будет выглядеть так:

. (3)

Закон изменения потенциальной энергии будет выглядеть так:

. (4)

С учётом (3) выражение (4) можно записать так:

. (5)

Из (5) находим момент времени, когда возвращающая сила и потенциальная энергия достигают заданные значения (учитываем, что величина синуса отрицательна при аргументах в интервале от  до 2):

.

Соответствующая фаза: .

Поверка размерностей:

;

или .

Задача 5.1.6

Водород в количестве 0,5 моль находится при температуре 300 К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию всех молекул этого газа.

Дано:

Найти:

Решение:

Средняя кинетическая энергия вращательного движения одной молекулы равна где- постоянная Больцмана,- число вращательных степеней свободы молекулы.

Для жесткой двухатомной молекулы , следовательно,

Суммарная кинетическая энергия всех молекул газа равна гдеN – число молекул газа, i – общее число степеней свободы молекулы.

Учитывая, что число молекул где- постоянная Авогадро, а число степеней свободыi = 5 (двухатомный газ), получаем:

…

…

Поверка размерностей: ,

.

Ответ:

Задача 5.1.7

10 г кислорода, находящегося при 0° С и давлении 10⁵ Па, сжимаются до объема 1,4 л. Найти давление и температуру кислорода после сжатия, если: а) кислород сжимается изотермически, б) кислород сжимается адиабатически. Определить работу сжатия в обоих случаях.

Дано:

m = 10 г

Найти:

Решение:

Начальная абсолютная температура газа

А) Изотермическое сжатие.

В изотермическом процессе

Давление получим из уравнения состояния идеального газа:

Молярная масса кислорода

Подставляя значения, получаем

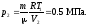
Работа, совершаемая газом, определяется выражением

Выражая из уравнения состояния давление, имеем:

Подставляя, получаем:

Учитывая, что получаем

Следовательно, над газом совершили работу

Б) Адиабатное сжатие.

Начальный объем газа равен

Уравнение адиабатного процесса имеет вид гдеi – число степеней свободы молекул газа (для кислорода (двухатомный газ) число степеней свободы молекулы i = 5).

Соответственно,

Конечное давление равно, соответственно,

Согласно первому началу термодинамики где- приращение внутренней энергии газа,А – работа, совершаемая газом.

В адиабатном процессе Q = 0, следовательно,

_{Следовательно, над газом совершили работу}

А)

…

…

…

Б)

…

…

…

…

…

Поверка размерностей:

;

;

;

;

.

Ответ: а) б)