Тема №6: «Финансовые посредники и финансовые вычисления: рынок ценных бумаг»
Задача 1
Бескупонная облигация будет погашена через A лет и B месяцев. Текущий курс K. Найти (сложную) доходность к погашению i.
|
Вариант |
Через сколько лет А и месяцев В будет погашена облигация |
Текущий курс К облигации | ||
|
A |
B | |||
|
3 |
7 |
4 |
55,00 | |
Доходность к погашению находиться с помощью соотношения
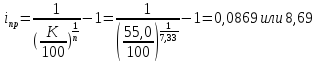
Задача 2
Найти доходность к погашению бескупонной облигации (сложную доходность), если рыночная цена сегодня — P руб., облигация погашается по номиналу N руб. через A лет В месяцев. Какова простая ставка доходности по облигации?
|
Вариант |
Через сколько лет А и месяцев В будет погашена облигация |
Рыночная цена P облигации, руб. |
Номинал N облигации, руб. | |||
|
A |
B | |||||
|
3 |
2 |
8 |
850 |
1000 | ||
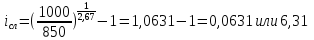
Задача 3
Срок облигации с фиксированным купоном равен n годам. Купонный доход выплачивается ежегодно по норме c% от номинала в год. Найти курс облигации, если ставка дисконтирования равна i%.
Указание. Сначала нужно вывести формулу для курса данного типа облигаций с использованием общей формулы для курса облигаций и формулы (6).
|
Вариант |
Срок облигации n, лет |
Купонный доход в % от номинала c, % |
Ставка дисконтирования i, % |
|
3 |
5 |
11,00 |
13,00 |
;
;
;
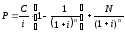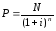Задача 4
Цена акции в начале периода составляет P1 руб., в конце периода – P2 руб. Суммарный дивидендный доход за данный период – Div руб., дивидендный доход за последний год рассматриваемого периода равен div руб. Определить доходность акции за рассматриваемый период, дивидендную доходность акции в конце рассматриваемого периода. Убыточны или прибыльны инвестиции в данную акцию на протяжении рассматриваемого периода?
|
Вариант |
P1 |
P2 |
Div |
div |
|
3 |
150 |
170 |
20 |
3 |
Задача 5
Последний годовой дивиденд акции составил d руб. Предполагается, что дивидендные доходы и стоимость акции будут возрастать с годовым темпом g%. Определить расчетную стоимость акции с использованием модели постоянного роста дивидендов, если ставка дисконтирования выбрана i%. Переоценена или недооценена акция рынком, если текущая рыночная цена акции составляет R руб.?
|
Вариант |
d, руб. |
g, % |
i, % |
R, руб. |
|
3 |
15 |
12 |
21 |
180 |
P=186,67; R=180, таким образом P>R, значит акция переоценена рынком.
Задача 6
А) Стоимость портфеля А в начале периода составляет P1, в конце периода – P1n. Стоимость портфеля B в начале этого же периода составляет P2, в конце этого же периода – P2n. Какой портфель предпочтительнее в терминах текущей доходности портфеля (рассчитать и сравнить текущие доходности в %)?
Б) Финансовый год (база) равен 365 дней. Период инвестирования для портфеля А равен n1, период инвестирования для портфеля B равен n2. Какой портфель предпочтительнее в терминах показателя доходности за период в расчете на год (в %)? Стоимости портфелей А и В в начале и конце периодов взять из п. А) данной задачи.
|
Вариант |
P1 |
P1n |
P2 |
P2n |
n1 |
n2 |
|
3 |
120 |
155 |
55 |
120 |
800 |
750 |
А)
Доходность портфеля А:
Доходность
портфеля В:
Портфель В предпочтительнее в терминах текущей доходности.
Б) Доходность портфеля А за год:
13,34%
Доходность портфеля В за год:
57,82%
Портфель В предпочтительнее в терминах показателя доходности за период в расчете на год.
Задача 7
Портфель 1 состоит из трех активов А, В и С с удельными весами 1A, 1B и 1C соответственно. Ожидаемые (средние за период) доходности активов А, В и С равны rA%, rB%, rC%. Портфель 2 состоит из двух активов F и H с удельными весами 2F и 2H соответственно. Ожидаемые (средние за период) доходности активов F и H равны rF%, rH%. Каков портфель предпочтительнее в терминах ожидаемой доходности портфеля (рассчитать ожидаемые доходности и сравнить портфели)?
|
Вариант |
A |
B |
C |
F |
H | |||||||||
|
1A |
rA |
1B |
rB |
1C |
rC |
2F |
rF |
2H |
rH | |||||
|
3 |
0,15 |
25,00 |
0,40 |
13,00 |
0,45 |
18,00 |
0,35 |
25,00 |
0,65 |
20,00 | ||||
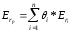
Ожидаемая доходность портфеля 1
)=0,1705
или 17,05%
Ожидаемая доходность портфеля 2
0,2175
или 21,75%
Портфель 2 предпочтительнее в терминах ожидаемой доходности
Задача 8
Портфель состоит из активов X и Y. Инвестор купил актив X на SX тыс. руб., актив Y на SY тыс. руб. Стандартное отклонение доходности актива X в расчете на год StX%, актива StY%, коэффициент корреляции доходностей активов Ro1. Определить риск портфеля, измеренный стандартным отклонением. Как изменится риск портфеля (вырастет, снизится, не изменится) если коэффициент корреляции доходностей изменится до Ro2?
|
Вариант |
X |
Y |
Ro1 |
Ro2 | |||||
|
SX |
StX |
SY |
StY | ||||||
|
3 |
350,00 |
17,00 |
800,00 |
25,00 |
0,40 |
0,30 | |||
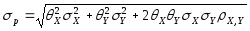
При уменьшении коэффициент корреляции доходностей между активами X и Y, риск портфеля тоже снизиться.