2 Проектирование зубчатой передачи

2.1 Схема редуктора и исходные данные

Рисунок 3 – Задание №2

Для механического редуктора дано:

В задании дана отдельная планетарная передача и отдельная простая передача

Рекомендуемое передаточное отношение для планетарной ступени

;

2.2 Определение передаточных отношений

Передаточное отношение редуктора равно

2.3 Расчет простой передачи

2.3.1 Подбор чисел зубьев колес

Числа зубьев простой передачи определяем из 3-х уравнений:

1. межцентрового расстояния:

2. передаточного отношения:

3. условия сборки:

Принимаем,тогда решая систему уравнений получаем следующее:

Принимаем:z₂ = 21;

Принимаем: z₁ = 14;

Принимаем: z₃= 56.

2.3.2 Расчет геометрии зацепления

подреза нет;

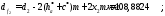
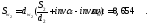
2.3.3 Определение качественных показателей зацепления

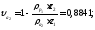
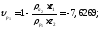
2.3.4 Длина общей нормали

Принимаем z_n1 = 2;

Принимаем z_n5 = 3;

2.4 Расчет планетарной передачи

2.4.1 Подбор чисел зубьев колес

Числа зубьев колес определяем по формуле

Принимаем

где а_n– число сателлитов.

Колеса планетарной ступени стандартные, поэтому d_wi=d_i

2.4.2 Проверка передаточного отношения, условия соосности, соседства и сборки

Условие соосности:

условие соосности выполняется.

Условие соседства

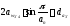, где

- межосевое расстояние

- радиус делительной окружности

Получаем:

условие соседства выполняется.

Условие сборки:

- целое число ,т.е. условие сборки выполняется.

2.5 Линейные и угловые скорости передачи

Для построения картины линейных и угловых скоростей используем следующий расчет.

Скорость в полюсе зацепления колёс 1 и 2

- угловая скорость колеса 1.

получаем

Масштаб линейных скоростей

Масштаб угловых скоростей , где

- масштаб построения схемы редуктора.

Кинематическую схему строят в масштабе откладываяи диаметры начальных окружностей колёс.

2.6 Сравнительный анализ результатов и КПД редуктора

Сравниваем передаточные отношения и

погрешность графического определения :

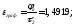
Определяем КПД редуктора :

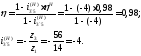
КПД всего редуктора: .

3 СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА

3.1 Исходные данные

Рисунок 4 – Задание №3

Закон движения толкателя

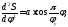
Фазовые углы, соответствующие фазам удаления, высоты и возвращения

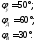
Ход толкателя

3.2 Аналитическое описание закона движения ведомого звена (аналитическое интегрирование) и расчет

Ускорение ведомого звена:

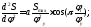
Функция является периодической. Рассмотрим интервал (0..).

Последовательно интегрируя получаем:

;

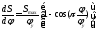
при

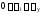
Аналогично получаем функции и для фазы возвращения.

Определим максимальное значение аналогов ускорений на фазах удаления и возвращения:

3.3 Выбор масштабов для построения графиков

, где

- результат расчетов,

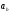- отрезок на чертеже.

, где

- результат расчетов,

- отрезок на чертеже.

Принимаем:

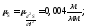
, где

- отрезок на чертеже, пропорциональный углу.

Отрезок делим на части пропорциональные углам,,.

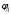3.4 Определение основных размеров кулачкового механизма

Для определения , строим диаграммупри

Размер определяем путем непосредственного измерения соответствующих отрезков на диаграмме

Расстояние от центра кулачка до направляющих ведомого звена определяется по формуле.

,

Длина направляющих

Радиус тарелки

Заключение

В работе выполнено исследование кинематики для компрессора.

Графоаналитическим способом определены скорости, ускорения точек и звеньев.

Высокая точность графических построений с помощью графического редактора «КОМПАС» позволила провести тщательное сравнение графоаналитического способа исследования с аналитическим.

В работе выполнено исследование кинематики зубчатой передачи. В ходе расчетов найдено:

Число зубьев простой передачи:

Числа зубьев планетарной ступени редуктора:

Передаточное отношение редуктора:

КПД редуктора:

Спроектирован кулачковый механизм.