
ФОСМС2015fokin_12345
.pdf
Непрерывный ряд Фурье периодической последовательности дельта импульсов
Последовательность дельта импульсов определяется выражением
|
= ∞=−∞ − |
(E1.1.7) |
|
= |
+∞ |
при = 0 |
(E1.1.7.1) |
0 при остальных |
|||
|
−∞+∞ = 1 |
(E1.1.7.2) |
|
По ф. (1.1.1b) оценим коэффициенты ряда Фурье
1.1.1 |
|
|
|
|
1.1.7 |
|
|
|
1.1.7.2 |
|
= |
|
|
|
− 0 |
= |
|
∞ |
− |
− 0 = 1 |
(E.1.1.8) |
|
|
|
|
|
|
=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
По ф. (1.1.1a) можем записать ряд Фурье последовательности дельта импульсов
1.1.1 |
1 |
∞ |
0 |
1.1.8 |
1 |
∞ |
0 |
|
= |
|
= |
|
(E1.1.9) |
||||
|
|
=−∞ |
|
|
|
=−∞ |
|
|
|
|
|
|
|
|
|
61
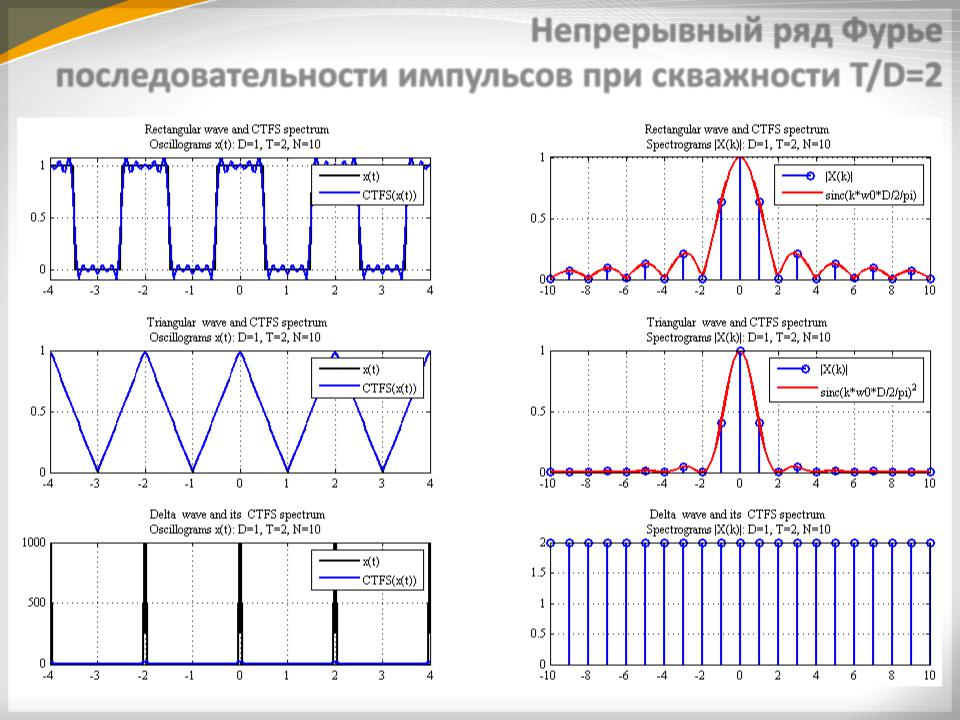
Непрерывный ряд Фурье последовательности импульсов при скважности T/D=2
62
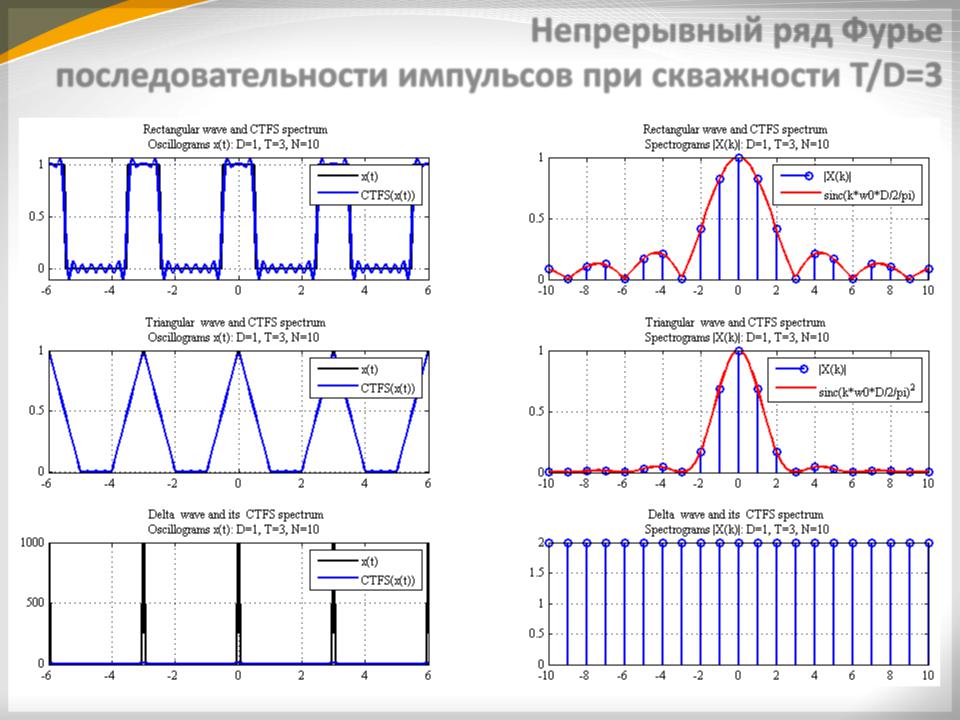
Непрерывный ряд Фурье последовательности импульсов при скважности T/D=3
63
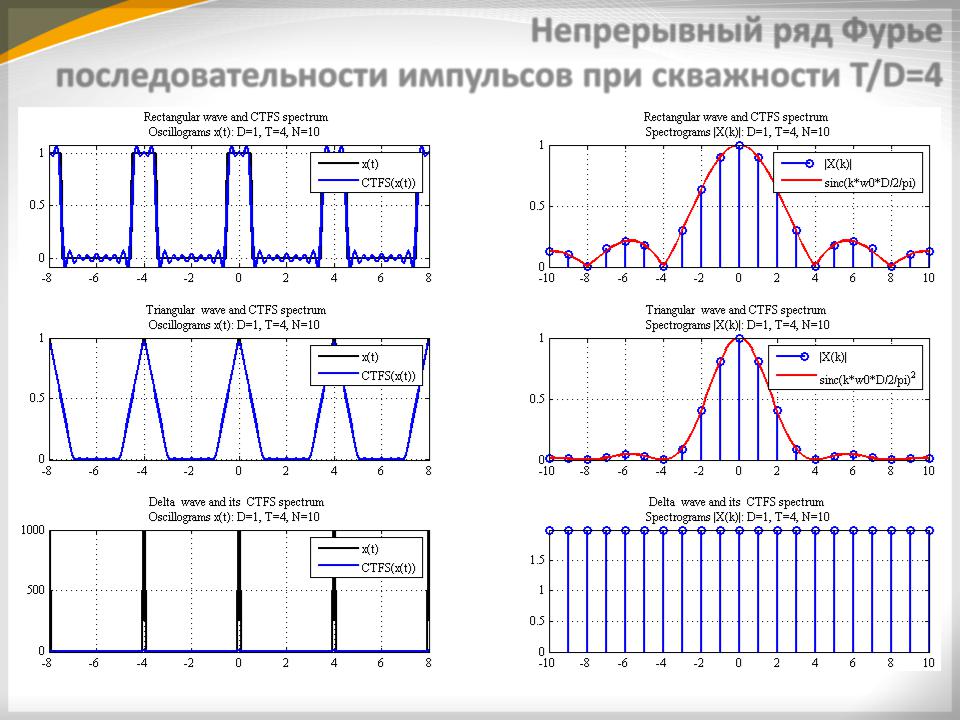
Непрерывный ряд Фурье последовательности импульсов при скважности T/D=4
64

Функция вычисления непрерывного ряда Фурье периодического сигнала
Функция CTFS вычисляет коэффициенты непрерывного ряда Фурье по ф. (1.1.1b) |
|
, = 0, … , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и сам ряд Фурье |
периодического сигнала по ф. (1.1.1a) с конечным числом коэффициентов |
|||||||||||
|
1.1.1 |
1 |
0 = 1 |
|
|
0 |
|
= |
|
|
||
|
= |
+ 2 |
при |
|
(1.1.2) |
|||||||
|
|
|
=− |
|
|
0 |
=1 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и рисует графики исходного сигнала |
и его ряда Фурье |
|
|
|
|
|||||||
function [Xk,kk,xht,tt]=CTFS(x,ng,str) global T D N
kk=[-N:N]; w0=2*pi/T; tt=[-2*T:2*T/100:2*T]; x=str2func(x);
xejkwt=@(t,k,w0)(x(t).*exp(-j*k*w0*t)); |
|
|
tol=0.001; |
|
|
for k=0:N |
|
|
X(k+1)=quadl(xejkwt,-T/2,T/2,tol,[],k,w0); |
% (1.1.1b) |
|
end |
|
|
Xk =[conj(X(N+1:-1:2)) X]; |
% to make the spectrum symmetric |
|
X_mag= abs(Xk); |
% Xph= angle(Xk); |
|
k=1:N; jkw0t=j*k.'*w0*tt; xht=(2*real(X(k+1)*exp(jkw0t))+X(1))/T; % (1.1.2) xt=feval(x,tt); % original signal subplot(ng); plot(tt,xt,'k-', tt,xht,'b-','linewidth',2);
str1=sprintf('Oscillograms x(t): D=%d, T=%d, N=%d ', D,T,N); title([str; str1]); legend('x(t)','CTFS(x(t))'); grid on; axis tight;
subplot(ng+1); stem(kk,X_mag,'LineWidth',2); |
grid on; axis tight; |
str2=sprintf('Spectrograms |X(k)|: D=%d, T=%d, N=%d', D,T,N); |
|
title([str; str2]); |
65 |

Функции осциллограмм и спектрограмм прямоугольных и треугольных импульсов
function x=rd_wave(t) global T D
tmp=min(abs(mod(t,T)),abs(mod(-t,T))); x=(tmp<=D/2);
function |
x=rd_wave_spectrum |
|
global T |
D N |
|
w0=2*pi/T; k1=linspace(-N,N); |
|
|
RD1=sinc(k1*w0*D/2/pi); |
% Spectrum |
|
hold on; |
plot(k1,abs(RD1),'r', 'linewidth',2); |
% Envelope for the spectrum |
legend('|X(k)|','sinc(k*w0*D/2/pi)'); |
|
|
function |
x=tri_wave(t) |
|
global T |
D |
|
tmpp=abs(mod(t,T)); tmpn=abs(mod(-t,T)); |
|
|
tmp= min(tmpp,tmpn); |
|
|
x=(tmp<=D).*(1-tmp/D); |
|
|
function |
x=tri_wave_spectrum |
|
global T |
D N |
|
w0=2*pi/T; k1=linspace(-N,N); |
|
|
Tri=sinc(k1*w0*D/2/pi); Tri1=Tri.*Tri; |
% Spectrum |
|
hold on, |
plot(k1,Tri1,'r', 'linewidth',2); |
% Envelope for the spectrum |
legend('|X(k)|','sinc(k*w0*D/2/pi)^2');
function x=delta_wave(t) global T D
tol=1e3; tmp=min(abs(mod(t,T)),abs(mod(-t,T))); x=tol*(tmp<=D/tol);
%dc01e01.m plots the CTFS spectra of rectangular,triangular and delta waves clear; clf;
global T D N D=1; T=4; N=10;
[Xk,kk,xht,tt]=CTFS('rd_wave',321, 'Rectangular wave and CTFS spectrum '); rd_wave_spectrum;
CTFS('tri_wave',323, 'Triangular wave and CTFS spectrum '); tri_wave_spectrum;
CTFS('delta_wave',325, 'Delta wave and its CTFS spectrum ');
66

Особенности непрерывного ряда Фурье последовательности периодических импульсов
Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени , описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала.
Совокупность величин называют комплексным спектром. Спектр периодического сигнала –
линейчатый. Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый arg спектры. Периодический сигнал удовлетворяет условию = + .
Сумма ряда (1.1.1a) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник
настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром . Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.
Если функция , описывающая периодический сигнал, является четной, то сумма ряда (1.1.1a) будет содержать только косинусоидальные составляющие. Если - нечетная функция, то сумма ряда (1.1.1a) будет содержать только синусоидальные составляющие.
Состав спектра периодической последовательности прямоугольных импульсов зависит от величины отношения периода последовательности к длительности импульса , называемого
скважностью импульсов. В спектре будут отсутствовать гармоники с номерами кратными скважности импульсов. Скважность импульсов равна = .
Разнос между соседними гармониками равен 0 = 2 .
Для периодической последовательности, скважность которой равна = 2, в спектре отсутствуют 2, 4, 6 ,8 и т. д. гармоники. Для последовательности с = 3, в спектре отсутствуют 3, 6 и т. д. гармоники. Для последовательности с = 4, в спектре отсутствуют 4, 8 и т. д. гармоники. В приведенных спектрах интервал между спектральными линиями равен величине обратной
периоду последовательности. Точки на оси частот, в которых спектр равен нулю, соответствуют
величине, обратной длительности импульсов периодических последовательностей. |
67 |

ччч
ччч
68
