
kalashnikov_tom_1
.pdf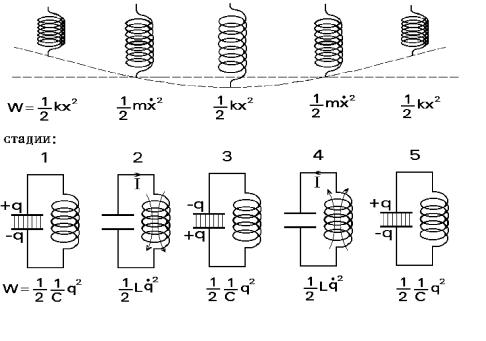
19.4. «®¦¥¨¥ ¯ à ««¥«ìëå ª®«¥¡ ¨© |
441 |
¨á. 19.9: §¬¥¥¨ï ¢® ¢à¥¬¥¨ à §«¨çëå ä®à¬ í¥à£¨¨ ¢ ª®«¥¡ ⥫쮩 á¨á⥬¥.
«®¦¥¨¥ ª®«¥¡ ¨© á ®¤¨ ª®¢ë¬¨ ç áâ®â ¬¨
«ï ¯à®áâ®âë à áᬮâਬ á ç « á«ãç ©, ª®£¤ ç áâ®âë ᪫ ¤ë¢ ¥¬ëå ª®«¥¡ ¨© ®¤¨ ª®¢ë. ¡é¨¥ à¥è¥¨ï ᪫ ¤ë¢ ¥¬ëå £ ମ¨ç¥áª¨å ª®- «¥¡ ¨© ¨¬¥îâ ¢¨¤:
x1 |
= |
A1 cos(!0t + 1) |
|
x2 |
= |
A2 cos(!0t + 2) |
(19.34) |
£¤¥ x1 x2 | ¯¥à¥¬¥ë¥, ®¯¨áë¢ î騥 ª®«¥¡ ¨ï, A1 A2 | ¨å |
¬¯«¨- |
||
âã¤ë, 1 2 | ç «ìë¥ ä §ë. ¥§ã«ìâ¨àãî饥 ª®«¥¡ ¨¥ x = x1+x2 㤮¡® ©â¨ á ¯®¬®éìî ¢¥ªâ®à®© ¤¨ £à ¬¬ë. â®â ¬¥â®¤ ¨á¯®«ì§ã¥â
«®£¨î ¬¥¦¤ã ¢à 饨¥¬ ¨ ª®«¥¡ ⥫ìë¬ ¯à®æ¥áᮬ.
®§ì¬¥¬ ®¡é¥¥ à¥è¥¨¥ (19.23) ¤«ï £ ମ¨ç¥áª®£® ª®«¥¡ ¨ï. ë¡¥- ६ ®áì Ox. § â®çª¨ O ®â«®¦¨¬ ¢¥ªâ®à ¤«¨®© A, ®¡à §ãî騩 á ®áìî
Ox 㣮« . ᫨ ¯à¨¢¥á⨠íâ®â ¢¥ªâ®à ¢® ¢à 饨¥ á 㣫®¢®© ᪮à®áâìî
!0, â® ¯à®¥ªæ¨ï ª®æ í⮣® ¢¥ªâ®à ¡ã¤¥â ¯¥à¥¬¥é âìáï ¯® ®á¨ Ox ®â +A ¤® ;A, ¯а¨з¥¬ ¢¥«¨з¨ ¯а®¥ªж¨¨ ¡г¤¥в ¨§¬¥пвмбп ¯® § ª®г
x(t) = A cos(!0t + ): |
(19.35) |
ª¨¬ ®¡à §®¬, ¯à®¥ªæ¨ï ª®æ ¢¥ªâ®à ®áì Ox ¡ã¤¥â ᮢ¥àè âì £ à- ¬®¨ç¥áª¨¥ ª®«¥¡ ¨ï á ¬¯«¨â㤮©, à ¢®© ¤«¨¥ ¢¥ªâ®à , á ªà㣮¢®©

442 |
« ¢ 19. ®«¥¡ ⥫쮥 ¤¢¨¦¥¨¥ |
ç áâ®â®©, à ¢®© 㣫®¢®© ᪮à®á⨠¢à é¥¨ï ¢¥ªâ®à , ¨ á ç «ì®© ä - §®©, à ¢®© 㣫ã, ®¡à §ã¥¬®¬ã ¢¥ªâ®à®¬ á ®áìî ¢ ç «ìë© ¬®¬¥â ¢à¥-
¬¥¨ (à¨á. 19.10).
¨á. 19.10: ¥ªâ®à ï ¤¨ £à ¬¬ ¤«ï ®¡é¥£® à¥è¥¨ï (19.23).
ਬ¥¨¬ ⥯¥àì íâã â¥å¨ªã ª á«®¦¥¨î ª®«¥¡ ¨© (19.34). ।áâ - |
|||||
¢¨¬ ®¡ |
|
|
~ |
~ |
|
ª®«¥¡ ¨ï á ¯®¬®éìî ¢¥ªâ®à®¢ A1 |
¨ A2. ®§ì¬¥¬ ¨å ¢¥ªâ®àãî |
||||
á㬬ã |
~ |
~ |
~ |
~ |
®áì Ox à ¢ á㬬¥ |
A = A1 |
+ A2 (à¨á. 19.11). ஥ªæ¨ï A |
||||
¯à®¥ªæ¨©: x = x1 + x2. ª¨¬ ®¡à §®¬, ¢¥ªâ®à |
~ |
||||
A ¯à¥¤áâ ¢«ï¥â ᮡ®© |
|||||
१ã«ìâ¨àãî饥 ª®«¥¡ ¨¥. â®â ¢¥ªâ®à ¢à é ¥âáï á ⮩ ¦¥ 㣫®¢®© ᪮à®áâìî !0, â ª ç⮠१ã«ìâ¨àãî饥 ¤¢¨¦¥¨¥ ¡ã¤¥â £ ମ¨ç¥áª¨¬ ª®«¥¡ ¨¥¬ á ç áâ®â®© !0, ¬¯«¨â㤮© A ¨ ç «ì®© ä §®© . ¬¥¥¬ ᮣ« ᮠ⥮६¥ ª®á¨ãᮢ:
A2 |
= |
A12 + A22 + 2A1A2 cos( 1 |
; |
2) |
|||
|
|
|
A1 sin 1 |
+ A2 sin 2 |
|
|
|
tg |
= |
|
: |
|
(19.36) |
||
|
A1 cos 1 |
|
|
||||
|
|
|
+ A2 cos 2 |
|
|
||
ç áâ®áâ¨, ¥á«¨ ä §ë ᪫ |
¤ë¢ ¥¬ëå ª®«¥¡ ¨© à ¢ë ¨«¨ ®â«¨ç îâáï |
|
ç¥â®¥ ªà ⮥ ( 1 |
; |
2 = 2 n), â® ¬¯«¨â㤠१ã«ìâ¨àãî饣® |
ª®«¥¡ ¨ï à ¢ á㬬¥ |
¬¯«¨â㤠A = A1 + A2. ᫨ ᪫ ¤ë¢ ¥¬ë¥ |
|
ª®«¥¡ ¨ï 室ïâáï ¢ ¯à®â¨¢®ä §¥ ( 1 ; 2 = (2n+1) ), â® A = jA1;A2j.
¨¥¨ï
í⮬ à §¤¥«¥ ¬ë à áᬮâਬ á«ãç © á«®¦¥¨ï ®¤¨ ª®¢® ¯à ¢«¥- ëå £ ମ¨ç¥áª¨å ª®«¥¡ ¨© á à §ë¬¨ ç áâ®â ¬¨. ¯à ªâ¨ª¥ ®á®- ¡ë© ¨â¥à¥á ¯à¥¤áâ ¢«ï¥â á«ãç ©, ª®£¤ ᪫ ¤ë¢ ¥¬ë¥ ª®«¥¡ ¨ï ¬ «® ®â«¨ç îâáï ¯® ç áâ®â¥. ª ¬ë 㢨¤¨¬, ¢ १ã«ìâ ⥠᫮¦¥¨ï íâ¨å

19.4. «®¦¥¨¥ ¯ à ««¥«ìëå ª®«¥¡ ¨© |
443 |
¨á. 19.11: ¥ªâ®à ï ¤¨ £à ¬¬ ¤«ï á«®¦¥¨ï ®¤¨ ª®¢® ¯à ¢«¥ëå ª®«¥¡ ¨©.
¨á. 19.12: ¨¥¨ï ¯à¨ á«®¦¥¨¨ ª®«¥¡ ¨© á ¡«¨§ª¨¬¨ ç áâ®â ¬¨.
ª®«¥¡ ¨© ¯®«ãç îâáï ª®«¥¡ ¨ï á ¯¥à¨®¤¨ç¥áª¨ ¨§¬¥ïî饩áï ¬¯«¨- â㤮©. ¥à¨®¤¨ç¥áª®¥ ¨§¬¥¥¨¥ ¬¯«¨âã¤ë ª®«¥¡ ¨©, ¢®§¨ª î饥 ¯à¨ á«®¦¥¨¨ ¤¢ãå £ ମ¨ç¥áª¨å ª®«¥¡ ¨© á ¡«¨§ª¨¬¨ ç áâ®â ¬¨, -
§ë¢ ¥âáï ¡¨¥¨ï¬¨.
«ï ¯à®áâ®âë à áᬮâਬ á«ãç ©, ª®£¤ ¬¯«¨âã¤ë ᪫ ¤ë¢ ¥¬ëå ª®«¥¡ ¨© à ¢ë A, ç «ìë¥ ä §ë ®¡®¨å ª®«¥¡ ¨© à ¢ë ã«î.áâ®âë ᪫ ¤ë¢ ¥¬ëå ª®«¥¡ ¨© à ¢ë, ᮮ⢥âá⢥®, ! ¨ ! + !.â ª,
x1 = A cos !t x2 = A cos(! + !)t: |
(19.37) |
ª« ¤ë¢ ¥¬ í⨠¢ëà ¦¥¨ï ¨ ãç¨âë¢ ¥¬ ¨§¢¥áâãî ä®à¬ã«ã âਣ®®-

444 « ¢ 19. ®«¥¡ ⥫쮥 ¤¢¨¦¥¨¥
¬¥âਨ:
x |
= A (cos !t + cos(! + !)t) = |
|
||||
|
! |
|
|
|
||
|
= 2A cos |
|
|
t cos(! + !=2)t: |
(19.38) |
|
᫨ ! !, â® ¢ |
2 |
|
||||
à£ã¬¥â¥ ¢â®à®£® ª®á¨ãá ¬ë ¬®¦¥¬ ¯à¥¥¡à¥çì |
||||||
ᤢ¨£®¬ ç áâ®âë: |
|
|
|
|
|
|
|
! |
|
|
|||
|
x 2A cos |
|
t cos !t: |
(19.39) |
||
|
2 |
|||||
஬¥ ⮣®, ¬®¦¨â¥«ì ¢ ᪮¡ª å ¬¥ï¥âáï ¬¥¤«¥® ¯® áà ¢¥¨î á |
||||||
cos !t. ®í⮬ã १ã«ìâ¨àãî饥 ª®«¥¡ ¨¥ x ¬®¦® à áᬠâਢ âì ª ª
£ ମ¨ç¥áª®¥ ª®«¥¡ ¨¥ á ç áâ®â®© !, íä䥪⨢ ï ¬¯«¨â㤠Aeff ª®- |
||||
â®à®£® ¨§¬¥ï¥âáï á® ¢à¥¬¥¥¬ (à¨á. 19.12): |
|
|||
|
! |
|
||
|
Aeff = j2A cos 2 tj: |
(19.40) |
||
áâ®â ¯ã«ìá 権 |
¬¯«¨âã¤ë (¥¥ §ë¢ îâ ç áâ®â®© ¡¨¥¨©) |
à ¢ |
||
à §®á⨠ç áâ®â ᪫ ¤ë¢ ¥¬ëå ª®«¥¡ ¨©. ¥à¨®¤ ¡¨¥¨© à ¢¥ |
|
|||
|
2 |
: |
(19.41) |
|
|
T = |
|
||
|
! |
|||
®«¥¡ ¨ï ¤¢ãå á¢ï§ ëå ®á樫«ïâ®à®¢ |
|
|||
ਢ¥¤¥¬ ¯®ãç¨â¥«ìë© ¯à¨¬¥à á¨á⥬ë, ¢ ª®â®à®© ¢®§¨ª îâ ¡¨¥¨ï. |
||||
áᬮâਬ ¤¢ £à㧠|
¬ áᮩ m, ª®â®àë¥ ¬®£ãâ ª®«¥¡ âìáï ¯® ¤¥©á⢨¥¬ |
|||
¤¢ãå ®¤¨ ª®¢ëå ¯à㦨 á ª®íää¨æ¨¥â ¬¨ ¦¥á⪮á⨠k. ãáâì £àã§ë ᮥ¤¨¥ë â ª¦¥ ¬ï£ª®© ¯à㦨®© á ª®íää¨æ¨¥â®¬ ¦¥á⪮á⨠k.㤥¬ ¯®« £ âì ¤«¨ë ¢á¥å ¯à㦨 ¢ ¥à áâïã⮬ á®áâ®ï¨¨ ®¤¨ -
ª®¢ë¬¨ ¨ à ¢ë¬¨ 2L (à¨á. 19.13). |
®£¤ |
¢ ¯®«®¦¥¨¨ à ¢®¢¥á¨ï ª®- |
||||||||
®à¤¨ âë £à㧮¢ à ¢ë x1 à ¢ = ;L, x2 à ¢ |
= L. ਠª®«¥¡ ¨ïå ª®®à- |
|||||||||
¤¨ âë à ¢ë, ᮮ⢥âá⢥®, x1(t) x2(t). ¤«¨¥¨ï ¯à㦨 § ¯¨- |
||||||||||
áë¢ îâáï ª ª |
x1 = x1 + L ( |
¤«ï «¥¢®© |
), x2 = x2 ; L ( |
¤«ï ¯à ¢®© |
) |
¨ |
||||
x3 = x2 ; x1 |
|
|
|
|
|
|||||
; 2L (¤«ï á।¥©). |
|
|
|
|
|
|
|
|||
|
ë ¨¬¥¥¬ ¤¥«® á á¨á⥬®© á ¤¢ã¬ï á⥯¥ï¬¨ ᢮¡®¤ë. |
®áâ ¢¨¬ |
||||||||
ãà ¢¥¨ï ¤¢¨¦¥¨ï. ¯¥à¢ë© £à㧠¤¥©áâ¢ãîâ: 1) ᨫ |
á® áâ®à®ë |
|||||||||
¯à㦨ë k [F1 = ;k(x1+L)] ¨ 2) ᨫ |
á® áâ®à®ë ¯à㦨ë [F12 = (x2; |
|||||||||
x1 |
;2L)]. ¢â®à®© £à㧠¤¥©áâ¢ãîâ |
«®£¨çë¥ á¨«ë: F2 = ;k(x2 ;L) |
||||||||
¨ |
F21 = ; (x2 |
; x1 ; 2L). ®®â¢¥âá⢥®, ãà ¢¥¨ï ¤¢¨¦¥¨ï ¨¬¥îâ |
||||||||
¢¨¤: |
|
|
|
|
|
|
|
|
|
|

19.4. «®¦¥¨¥ ¯ à ««¥«ìëå ª®«¥¡ ¨© |
445 |
¨á. 19.13: ਬ¥à á¢ï§ ëå ®á樫«ïâ®à®¢. ®«¥¡ ¨ï ¯à®¨á室ïâ ¢¤®«ì ®á¨ Ox, ᨫ â殮á⨠¥ ãç¨âë¢ ¥âáï.
mx1 |
= |
;k(x1 + L) + (x2 ; x1 ; 2L) |
|
mx2 |
= |
;k(x2 ; L) ; (x2 ; x1 ; 2L): |
(19.42) |
⨠ãà ¢¥¨ï ¥ ᫨誮¬ ¯®å®¦¨ ¯¥à¢ë© ¢§£«ï¤ ãà ¢¥¨ï £ à- ¬®¨ç¥áª¨å ª®«¥¡ ¨©, ¯®â®¬ã çâ® ª®«¥¡ ¨ï x1 ®ª §ë¢ îâ ¢«¨ï¨ï ª®«¥¡ ¨ï x2 ¨ ®¡®à®â. ®í⮬㠯८¡à §ã¥¬ ãà ¢¥¨ï ª ®¢ë¬ ¯¥à¥- ¬¥ë¬, ª®«¥¡ ¨ï ª®â®àëå ¡ë«¨ ¡ë ¥§ ¢¨á¨¬ë¬¨ (â ª¨¥ ¯¥à¥¬¥ë¥ §ë¢ î⠮ଠ«ì묨 ¬®¤ ¬¨). ¬¥®, ¢¢¥¤¥¬ ®¢ë¥ ¯¥à¥¬¥ë¥ 1
¨ 2:
1 |
= x2 ; x1 |
; |
L 2 |
= x1 + x2 |
|
|
|
2 |
|
2 |
|
|
|
x1 |
= 2 ; 1 ; L x2 |
= 1 + 2 + L: |
(19.43) |
|||
ª «¥£ª® ã¡¥¤¨âìáï, ¯®«®¦¥¨î à ¢®¢¥á¨ï ᮮ⢥âáâ¢ãîâ ª®®à¤¨ âë
1 à ¢ = 2 à ¢ = 0.
íâ¨å ¯¥à¥¬¥ëå ãà ¢¥¨ï (19.42) ¯à¨¨¬ îâ ¢¨¤:
|
|
;k( 2 ; 1) + 2 1 |
|
m( 2 |
; 1) = |
|
|
m( 2 + 1) = |
;k( 2 + 1) ; 2 1: |
(19.44) |
|
ª« ¤ë¢ ï ¨ ¢ëç¨â ï í⨠ãà ¢¥¨ï, ¯à¨å®¤¨¬ ª ¯ ॠ¥§ ¢¨á¨¬ëå ãà ¢- ¥¨© ¤«ï ª®«¥¡ ¨© ®à¬ «ìëå ¬®¤:
|
= |
|
k 2 |
|
m 2 |
; |
|
||
|
|
|
|
|
m 1 |
= |
;(k + 2 ) 1: |
(19.45) |
|
¥à¢®¥ ãà ¢¥¨¥ ®¯¨áë¢ ¥â £ ମ¨ç¥áª¨¥ ª®«¥¡ ¨ï á ç áâ®â®© !0 = pk=m, ᮢ¯ ¤ î饩 á ç áâ®â®© ª®«¥¡ ¨© ¯à㦨ëå ¬ ï⨪®¢ ¢ ®â- бгвбв¢¨¥ б®¥¤¨¨в¥«м®© ¯аг¦¨л . â®à®¥ ãà ¢¥¨¥ ®¯¨áë¢ ¥â ª®«¥-


19.4. «®¦¥¨¥ ¯ à ««¥«ìëå ª®«¥¡ ¨© |
447 |
¨á. 19.14: ¨¥¨ï ¢ á¨á⥬¥ ¤¢ãå á¢ï§ ëå ®á樫«ïâ®à®¢.
à 䨪¨ äãªæ¨© x1(t) x2(t) á¬. à¨á. 19.14. ç «ìë© ¬®¬¥â ¢à¥- ¬¥¨ ª®«¥¡«¥âáï «¨èì ¯¥à¢ë© £àã§. ⥬ ç¨ ¥â ª®«¥¡ âìáï ¢â®à®©,
¬¯«¨â㤠ª®«¥¡ ¨© ¯¥à¢®£® 㬥ìè ¥âáï. ¥à¥§ ¢à¥¬ï t = = ! ¯¥à¢ë© £à㧠®áâ ¢«¨¢ ¥âáï, ¢â®à®© ª®«¥¡«¥âáï á ¬ ªá¨¬ «ì® ¢®§- ¬®¦®© ¬¯«¨â㤮©. ந§®è« \¯¥à¥ª çª " í¥à£¨¨ ®â ¯¥à¢®£® ¬ ïâ- ¨ª ª® ¢â®à®¬ã. ⥬ ¯à®æ¥áá \¯¥à¥ª 窨" í¥à£¨¨ ¨¤¥â ¢ ®¡à ⮬ ¯à ¢«¥¨¨ ¨ ª ¬®¬¥âã t = 2 = ! ¯¥à¢ë© ¬ ï⨪ ª®«¥¡«¥âáï á ¬ ª- ᨬ «ì®© ¬¯«¨â㤮©, ¢â®à®© ¯®ª®¨âáï.
ëïᨬ ⥯¥àì 䨧¨ç¥áª¨© á¬ëá« ®à¬ «ìëå ¬®¤, ᮮ⢥âáâ¢ãî- é¨å ç¨áâ® £ ମ¨ç¥áª¨¬ ª®«¥¡ ¨ï¬ á¨á⥬ë. ᫨ ¢®§¡ã¦¤¥ë ª®- «¥¡ ¨ï ⮫쪮 ¯¥à¢®© ¨§ ¨å ( 1), â® A2 = 0 ¨, ª ª á«¥¤ã¥â ¨§ ®¡é¥£®
à¥è¥¨ï (19.48), |
|
|
|
x1 |
= |
;L ; A1 cos[(!0 + !)t + 1] |
|
x2 |
= |
L + A1 cos[(!0 + !)t + 1]: |
(19.53) |
묨 á«®¢ ¬¨, ¯¥à¢ ï ®à¬ «ì ï ¬®¤ ᮮ⢥âáâ¢ã¥â â ª®¬ã ª®«¥¡ - ¨î, ª®£¤ ®¡ £à㧠ᬥé îâáï ®¤¨ ª®¢ë¥ à ááâ®ï¨ï ®â ¨å ¯®«®- ¦¥¨© à ¢®¢¥á¨ï, ® ¢ ¯à®â¨¢®¯®«®¦ë¥ áâ®à®ë. ª®à®á⨠¤¢¨¦¥¨ï £à㧮¢ â ª¦¥ à ¢ë ¯® ¢¥«¨ç¨¥ ¨ ¯à®â¨¢®¯®«®¦ë ¯® ¯à ¢«¥¨î, â ª çâ® æ¥âà ¬ áá £à㧮¢ ®áâ ¥âáï ¥¯®¤¢¨¦ë¬. ®«¥¡ ¨ï ¯à®¨á- 室ïâ ¯®¤ ¤¥©á⢨¥¬ ¯à㦨 á ¦¥á⪮áâìî k, ª ª®â®àë¬ ¤®¡ ¢«ï¥âáï ᮥ¤¨¨â¥«ì ï ¯à㦨 á ¦¥á⪮áâìî . ª á«¥¤á⢨¥, ç áâ®â â ª¨å ª®«¥¡ ¨© ¡®«ìè¥ ç áâ®âë ª®«¥¡ ¨© ¥á¢ï§ ëå ®á樫«ïâ®à®¢.
448 |
« ¢ 19. ®«¥¡ ⥫쮥 ¤¢¨¦¥¨¥ |
®§¡ã¦¤¥¨¥ ⮫쪮 ¢â®à®© ( 2) ®à¬ «ì®© ¬®¤ë ®§ ç ¥â, çâ® A1 =
0:
x1 |
= |
;L + A2 cos(!0t + 2) |
|
x2 |
= |
L + A2 cos(!0t + 2): |
(19.54) |
í⮬ á«ãç ¥ £àã§ë ᬥé îâáï ¨§ ¯®«®¦¥¨ï à ¢®¢¥á¨ï ¢ ®¤ã áâ®à®ã ®¤¨ ª®¢ë¥ à ááâ®ï¨ï. ª®à®á⨠¨å â ª¦¥ ®¤¨ ª®¢ë ¯® ¢¥«¨ç¨¥ ¨ ¯à ¢«¥¨î. ®¥¤¨¨â¥«ì ï ¯à㦨 ª®«¥¡«¥âáï ¢¬¥áâ¥ á £à㧠¬¨, ® ®áâ ¥âáï ¥ à áâïã⮩ ¨ ¯®â®¬ã ¥ ®ª §ë¢ ¥â ¢«¨ï¨ï, â ª çâ® ç áâ®â ª®«¥¡ ¨© ᮢ¯ ¤ ¥â á ç áâ®â®© ª®«¥¡ ¨© ¥á¢ï§ ëå ¬ ï⨪®¢.
à §®¡à ®¬ á«ãç ¥ ¬ë ¯®§ ª®¬¨«¨áì á ®à¬ «ì묨 ¬®¤ ¬¨ ¨ ¢ëïᨫ¨, çâ® ¨å ç áâ®âë ᤢ¨£ îâáï ¯® áà ¢¥¨î á ç áâ®â ¬¨ ª®«¥- ¡ ¨© ¥á¢ï§ ëå ¬ ï⨪®¢. î¡®¥ ¤à㣮¥ ª®«¥¡ ⥫쮥 ¤¢¨¦¥¨¥ á¨áâ¥¬ë ¬®¦® ¯à¥¤áâ ¢¨âì ª ª á㯥௮§¨æ¨î ®à¬ «ìëå ¬®¤. - «®£¨çë¬ ®¡à §®¬ ¬®¦® à áᬮâà¥âì 楯®çªã ¨§ ¬®¦¥á⢠á¢ï§ ëå ¤àã£ á ¤à㣮¬ ®á樫«ïâ®à®¢ ¨ ¨§ãç¨âì ¨å ®à¬ «ìë¥ ª®«¥¡ ¨ï. ª ï á¨á⥬ ¯à¥¤áâ ¢«ï¥â ᮡ®© ¬®¤¥«ì ªà¨áâ ««¨ç¥áª®© à¥è¥âª¨.
19.5«®¦¥¨¥ ¯¥à¯¥¤¨ªã«ïàëå ª®«¥¡ ¨©
í⮬ à §¤¥«¥ ¬ë à áᬮâਬ á«®¦¥¨¥ ¤¢ãå £ ମ¨ç¥áª¨å ª®«¥¡ ¨© ®¤¨ ª®¢®© ç áâ®âë !, ¯à®¨á室ïé¨å ¢® ¢§ ¨¬® ¯¥à¯¥¤¨ªã«ïàëå -
¯à ¢«¥¨ïå ¢¤®«ì ®á¥© x ¨ y. |
롥६ ç «® ®âáç¥â |
¢à¥¬¥¨ â ª, |
ç⮡ë ç «ì ï ä § ¯¥à¢®£® ª®«¥¡ ¨ï ¡ë« à ¢ ã«î: |
||
x = A cos !t |
y = B cos(!t + ) |
(19.55) |
£¤¥ | à §®áâì ä § ®¡®¨å ª®«¥¡ ¨©. ©¤¥¬ ãà ¢¥¨¥ âà ¥ªâ®à¨¨
ª®«¥¡«î饩áï ¬ â¥à¨ «ì®© â®çª¨, â.¥. äãªæ¨î y = y(x). |
|
áᬮâਬ á ç « ç áâë¥ á«ãç ¨. ãáâì à §®áâì ä § à ¢ |
ã«î: |
= 0. ®£¤ |
|
y = B x |
(19.56) |
A |
|
â.¥. âà ¥ªâ®à¨ï â®çª¨ ¯à¥¤áâ ¢«ï¥â ᮡ®© ¯àï¬ãî. «®£¨ç ï âà ¥ª- â®à¨ï ¯®«ãç¨âáï ¯à¨ ª®«¥¡ ¨ïå á à §®áâìî ä § = :
B
y = B cos(!t + ) = ;B cos(!t) = ;A x: (19.57)


450 |
« ¢ 19. ®«¥¡ ⥫쮥 ¤¢¨¦¥¨¥ |
¨á. 19.16: ਬ¥àë 䨣ãà ¨áá ¦ã ¤«ï 㪠§ ëå ®â®è¥¨© ç áâ®â ¨ ã«¥¢ëå § - 票© ç «ìëå ä § ª ¦¤®£® ª®«¥¡ ¨ï. ®®à¤¨ â x ¢ëà ¦¥ ¢ ¥¤¨¨æ å ¬¯«¨- âã¤ë ª®«¥¡ ¨© A, ª®®à¤¨ â y | ¢ ¥¤¨¨æ å ¬¯«¨âã¤ë B. áâ®â !1 ®â®á¨âáï ª ª®«¥¡ ¨ï¬ ¢¤®«ì ®á¨ x, !2 | ¢¤®«ì ®á¨ y.
ë ¯®«ã稫¨ ãà ¢¥¨¥ ¯ à ¡®«ë. ®à¬ 䨣ãà ¨áá ¦ã § ¢¨á¨â ®â á®- ®â®è¥¨ï ç áâ®â ᪫ ¤ë¢ ¥¬ëå ª®«¥¡ ¨© ¨ à §®áâ¨ ä § ¬¥¦¤ã ¨¬¨.ਬ¥àë ¯®ª § ë à¨á. 19.16 ¨ 19.17.
¨á. 19.17: ਬ¥àë 䨣ãà ¨áá ¦ã ¤«ï â¥å ¦¥ ®â®è¥¨© ç áâ®â, çâ® à¨á. 19.16 ¨ ®¤¨ ª®¢ëå ¦¥ ç «ìëå ä § å ª ¦¤®£® ª®«¥¡ ¨ï 1 = 2 = ; =2, â.¥. ¯à¨ x =
A sin !1t y = B sin !2t.
19.6¢®¡®¤ë¥ § âãå î騥 ª®«¥¡ ¨ï
ମ¨ç¥áª¨¥ ª®«¥¡ ¨ï, áãé¥áâ¢ãî騥 ¢¥ç®, п¢«повбп ®¤®© ¨§ д¨- §¨ç¥áª¨å ¡áâà ªæ¨©. ॠ«ìëå á¨á⥬ å ª®«¥¡ ¨ï ¯® ¯à®è¥á⢨¨ ¥ª®â®à®£® ¢à¥¬¥¨ § âãå îâ ¨§-§ ¤¨áᨯ 樨 í¥à£¨¨. ª¨¬ ®¡à §®¬, ¯à¥¤áâ ¢«¥¨¥¬ ® £ ମ¨ç¥áª¨å ª®«¥¡ ¨ïå ¬®¦® ¯®«ì§®¢ âìáï «¨èì
¤«ï ¢à¥¬¥, ¬ «ëå ¯® áà ¢¥¨î á å à ªâ¥àë¬ ¢à¥¬¥¥¬ § âãå ¨ï.âãå ¨¥ ª®«¥¡ ¨© ¢á¥£¤ ¡ã¤¥â ¡«î¤ âìáï ¢ á¨á⥬ å á â२¥¬.
