
Выч.мат
..pdfОтсюда, подставляя f1 в правую часть (5a), имеем:
f1 − |
f0 |
|
f0 |
+ hf0′ + |
|
h2 |
f0′′ − f0 |
h |
|
|
|
2 |
f0′′ + o(h) . |
||||||||
= |
|
|
|
+…= f0′ + |
||||||
h |
|
|
|
h |
|
2 |
||||
|
|
|
|
|
|
|
||||
Сравнивая с левой частью, получаем:
f0′ = |
f1 − f0 |
− |
h |
f0′′ − o(h) . |
(9) |
|
h |
2 |
|||||
|
|
|
|
погрешность
Здесь выражение o(h) объединяет слагаемые высшего порядка малости по сравнению с линейным членом. Найдем теперь погрешность в окрестности точки x1. Для этого необходимо разложить f0 в окрестности этой точки.
|
|
f0 = f (x0 )= f (x1 − h)= f1 |
− hf1′ + |
|
h2 |
f0′′ . |
||||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||
Подставим в исходную формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
f1 − |
f0 |
|
f1 − f1 |
+ hf1′ − |
h2 |
f1′′ |
|
|
h |
2 |
|
|
|||||||||
|
= |
2 |
|
|
= f1′ − |
|
|
f1′′− o(h) , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
h |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
|
|
|
f1 |
− f0 |
|
|
|
|
h |
|
|
|
|
|
|
|
|
||||
|
|
|
|
f1′ |
= |
+ |
|
f1′′+o(h) . |
(10) |
|||||||||||||
|
|
|
|
|
h |
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вновь мы получили линейную зависимость погрешности от шага h. Определение. Порядком точности приближенной формулы (например, формулы дифференцирования) называется число, равное показателю степени шага h старшего члена в погрешности этой формулы.
Например, формулы (9) и (10) являются формулами первого порядка точности. Можно показать, что все одночленные формулы имеют первый порядок точности (точнее, не ниже первого).
Пример 2. Вычислим погрешность одночленной формулы (6a) для второй производной в точках x0, x1, x2. В крайних точках интервала формула дифференцирования с учетом погрешности представляется в виде:
f0′′,2 |
= |
f0 − 2 f1 + f2 |
+ R(x) , |
(11) |
|
h2 |
|||||
|
|
|
|
где погрешность
R(x) = h | f0′′,′2 | .
31
Следовательно, в крайних узлах (11) является формулой первого порядка точности.
Определим теперь погрешность в среднем узле промежутка x1.Как и в случае формулы (9) − (11) предполагаем, что исходная функция обладает необходимым количеством производных для представления ее в виде ряда Тейлора. Разложим f0 и f2 в окрестности x1:
f0 = f (x1 − h)= |
f1 |
− hf1′ + |
|
h2 |
f1′′− |
|
h |
3 |
f1′′′+ |
|
h4 |
f |
(1V ) |
+... |
||||||
2 |
|
6 |
|
24 |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f2 = f (x1 + h)= |
f1 |
+ hf1′ |
+ |
h2 |
f1′′ |
+ |
h3 |
f1′′′+ |
h4 |
f |
|
(1V ) |
+... |
|||||||
2 |
|
6 |
|
|
24 |
|
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда имеем
f0 + f2 = 2 f1 + h |
2 |
f1′′+ |
h4 |
f |
(1V ) |
+ o(h |
4 |
) . |
|
12 |
1 |
|
|||||
|
|
|
|
|
|
|
Тогда формула численного дифференцирования приобретает вид
f |
|
− 2 f |
|
+ f |
|
|
h |
2 |
f1′′+ |
h4 |
f |
(1V ) |
+ o(h |
4 |
) |
|
|
h2 |
|
|
|
0 |
1 |
2 |
= |
|
12 |
1 |
|
= |
f1′′+ |
f |
(1V ) |
+ o(h2 ) . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||
|
|
h2 |
|
|
|
|
|
|
h2 |
|
|
|
12 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
И для точки x1 получаем:
f1′′= |
f0 −2 f1 + f 2 |
− |
h2 |
f |
(1V ) |
. |
(12) |
|
h2 |
12 |
1 |
||||||
|
|
|
|
|
Для средней точки промежутка погрешность оказалась пропорциональной не первой степени h , а квадрату шага h2, т.е. в средней точке одночленная формула второй производной имеет повышенную точность.
Эту особенность для формулы численного дифференцирования второго порядка можно прояснить, вернувшись к формулам дифференцирования интерполяционного многочлена. Используя (3) и (4), можем оценить погрешность одночленной формулы следующим образом:
|
|
R(x)= (ξ1 +ξ2 |
+ξ3 ) |
f ′′′ |
. |
|
|
|
|
|
|
||||
В средней точке имеем: |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
(ξ1 +ξ2 +ξ3 ) |
|
= (3x − x0 − x1 − x2 ) |
|
= 0 |
|||
|
|
||||||
|
|
x = x1 |
|
|
|
|
x = x1 |
и таким образом, линейное по h слагаемое в погрешности обращается в нуль, а учет следующего слагаемого в погрешности дает второй порядок точности формулы (12) в средней точке интервала.
32

Можно показать, что двучленные формулы численного дифференцирования имеют порядок точности не ниже второго.
4. Порядок точности формул численного дифференцирования функций ограниченной гладкости
Рассмотрим двучленную формулу первой производной
f1′ = |
f2 − f0 |
. |
(13) |
|
|||
|
2h |
|
|
Схема вычисления погрешности выглядит следующим образом: в правой части f2 и f0 разлагаем в ряд Тейлора в окрестности точ-
ки x1 и затем вычисляем выражение
R1 (f )= f1′ − f2 2h− f0 ,
которое и является погрешностью формулы численного дифферен-
цирования. Положим вначале, что функция f |
обладает необходи- |
||||||||||
мым количеством производных для представления в виде ряда |
|||||||||||
f2 = f (x2 )− f (x1 |
+ h)= f1 + hf1′ + |
h2 |
f1′′+ |
h3 |
f1′′′+ |
||||||
2 |
|
6 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
f0 = f (x0 )− f (x1 |
− h)= f1 − hf1′ + |
|
h2 |
f1′′− |
|
h3 |
f1′′′+ |
||||
|
2 |
|
|
6 |
|
||||||
Вычитая, имеем |
|
|
|
|
|
|
|
|
|
||
|
h3 |
|
|
|
|
|
|
|
|
|
|
f2 − |
f0 = 2hf1′ + |
f1′′′ . |
|
|
|
|
|
||||
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
И для погрешности находим
R1 (f )= f1′ − |
f2 − f0 |
|
|
|
|
h |
2 |
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
f ′′′, |
||||
2h |
= |
f1′ − |
|
f1′ + |
6 |
f1′′′ |
= − |
6 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. эта формула имеет второй порядок точности по шагу, однако
только в том случае, если функция f обладает по меньшей мере тремя непрерывными производными.
Если функция имеет только две непрерывные производные, тогда представление функции в виде ряда Тейлора не годится, и в общем случае следует использовать формулу Тейлора (8a), которая используется, когда функция имеет ограниченное число непрерывных производных до n- го порядка включительно. Если функция обладает только двумя непрерывными производными, то
f2 |
= f1 + hf1′ + |
h2 |
f ′′(ξ1 ) |
h <ξ1 < 2h |
|
2 |
|||||
|
|
|
|
33

f0 = f1 − hf1′ + |
|
h2 |
f ′′(ξ2 ) |
0 <ξ2 < h |
|||||
|
2 |
||||||||
и, следовательно, |
|
|
|
|
|
||||
|
h2 |
|
|
|
|
||||
f2 − f0 = 2hf1′ + |
|
|
[f ′′(ξ1 )− |
f ′′(ξ2 )]. |
|||||
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
||
В этом случае погрешность равна |
|
||||||||
R1 (f )= − |
h |
|
[f ′′(ξ1 )− f ′′(ξ2 )]. |
||||||
|
|||||||||
4 |
|
|
|
|
|
|
|
|
|
Поскольку точки ξ1 и ξ 2 принадлежат разным промежуткам, то, вообще говоря, правая часть предыдущего выражения не равна нулю, поэтому эта формула имеет только первый порядок точности по шагу, в том случае, если функция имеет непрерывные производные не выше второго порядка. Аналогичные вычисления можно провести и для формулы второй производной
f1′′= f0 − 2 f21 + f2 . h
Если здесь функция f имеет четвертую непрерывную производную, то предыдущая формула имеет второй порядок точности и ее погрешность равна
R2 = − h122 f (4)(ξ).
Однако, если у f есть только три непрерывные производные, то формула будет уже первого порядка точности.
Таким образом, порядок точности определяется не только взаимным расположением точек, но и гладкостью функции.
5. Оптимальный шаг дифференцирования
Во всех рассмотренных примерах вычисления погрешности было найдено, что точность результата численного дифференцирования растет с уменьшением шага сетки. Это так, если учитывать только погрешность метода. Однако во внимание следует принимать и погрешность округления, при этом оказывается, что чрезмерное измельчение сетки может привести к росту погрешности. Здесь сказывается присущая операции дифференцирования некорректность, точнее неустойчивость к входным данным, другими словами чувствительность к небольшим изменениям дифференцируемой функции. Рассмотрим поведение суммарной погрешности, складывающейся из вычислительной погрешности и погрешности метода
34

на примере вычисления первой производной по простейшей формуле, которую можно записать в виде
f ′ = |
af0 + bf1 + cf2 |
+ R . |
(14) |
|
h |
||||
|
|
|
Здесь погрешность метода R = α hn , где n = 1 или n = 2. Поскольку числа задаются приближенно, то и значения функции в узлах задаются с погрешностью fi +εi . Обозначим через ε максималь-
ную погрешность округления, тогда в (14) реально вычисляется величина
f |
′ |
= |
af0 + bf1 + cf2 |
+ |
βε |
+α h |
n |
. |
|
h |
h |
|
В этом выражении два последних слагаемых дают суммарную погрешность
∆ = |
βε |
+α hn |
, |
(15) |
|
h |
|
|
|
где β = |a| +|b| +|c|, ε = max εi. Видно, что суммарная погрешность растет как с увеличением, так и с уменьшением шага. График функции ∆(h) имеет минимум, который соответствует оптимальному шагу, минимизирующему значение погрешности.
Пример 3. Определим оптимальный шаг для формулы численного дифференцирования (13). Это формула второго порядка точности и ее наибольшая погрешность равна
R = |
h2 M 3 |
, |
M 3 = |
′′′ |
|
||||
6 |
max | f (x) | . |
|||
|
|
|
x [x0 ,x2 ] |
Суммарная погрешность, согласно (15), равна
∆(h) = εh + h26M 3 .
Положение минимума функции определяется равенством нулю ее производной ∆′(h) = 0. Выполняя дифференцирование, находим
− |
ε |
+ |
hM 3 |
=0 . |
h2 |
|
|||
|
3 |
|
||
Из последнего равенства определяем оптимальный шаг дифференцирования
hopt = (3ε M 3 )1/ 3 .
M 3 )1/ 3 .
35

Задачи
1. Вычислить значение первой производной функции, заданной таблично
i |
0 |
1 |
2 |
3 |
4 |
xi |
0.1 |
0.15 |
0.19 |
0.25 |
0.28 |
fi |
1.105 |
1.165 |
1.209 |
1.284 |
1.332 |
в точке x = 0.2 и оценить погрешность.
2. Вычислить значение первой производной во всех узлах функции заданной таблично
i |
0 |
1 |
2 |
3 |
4 |
5 |
xi |
1.4 |
1.6 |
1.8 |
2.0 |
2.2 |
2.4 |
fi |
1.3796 |
1.5993 |
1.7529 |
1.8186 |
1.7787 |
1.6211 |
с использованием конечно-разностных выражений:
а) первого порядка точности; b) второго порядка точности. Результат сравнить с данными для функции f (x) = x sin x .
3. Определить погрешность формулы численного дифференцирования R полагая, что все производные функции f непрерывны.
a) f1' = |
|
f2 − f0 |
+ R(x) , |
b) f2' = |
f0 − 4 f1 + 3 f2 |
+ R(x) , |
|||
|
2h |
2h |
|||||||
|
|
|
|
|
|
|
|
||
c) f1' = |
|
−2 f0 −3 f1 +6 f 2 − f3 |
+ R(x) , |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
6h |
|
|
|
|
d) f2' = |
|
f0 −6 f1 + 3 f2 + 2 f3 |
|
+ R(x) . |
|
|
|||
|
|
|
|
||||||
|
|
|
|
|
6h |
|
|
|
|
Определить порядок точности формулы, если f обладает непрерывными производными до второго порядка включительно.
4. Определить погрешность формулы численного дифференцирования R полагая, что все производные функции f непрерывны.
a) |
f2'' = |
f0 − 2 f1 + f2 |
+ R(x) |
, b) f1'' = |
f0 − 2 f1 + f2 |
+ R(x) , |
||
h2 |
h2 |
|||||||
|
|
|
|
|
|
|||
c) |
f0'' = |
2 f0 − 5 f1 + 4 f2 − f3 |
|
+ R(x) , |
|
|||
|
|
|
||||||
|
|
h2 |
|
|
|
|
|
|
d) f3'' = − f0 + 4 f1h−25 f2 + 2 f3 + R(x) .
Определить порядок точности формулы, если f обладает непрерывными производными до третьего порядка включительно.
5. Определить оптимальный шаг формулы численного дифференцирования
36
f1' = |
f2 − f0 |
, |
|
2h |
|||
|
|
если вычисления проводятся с четырьмя значащими цифрами (ε = 5 10 –5 ) для функций
a) |
f (x) = |
sin x |
, |
1 ≤ x ≤ 2; b) |
f (x) = |
cos x |
, |
1 ≤ x ≤ 2; |
|
|
x |
||||||||
|
|
1 |
x |
|
|
|
|
|
|
c) |
f (x) = |
, |
|
1 ≤ x ≤ 2. |
|
|
|
|
|
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
6. Получить формулу численного дифференцирования: a) третьей производной; b) четвертой производной в среднем узле по пяти точкам равномерной сетки.
7. Определить порядок точности формулы численного дифференцирования
' |
|
f2 − f0 |
|
f1 |
= |
|
|
2h |
|||
|
|
для функции
|
+ 3x |
− 2x |
2 |
+ x |
3 |
, |
0 ≤ x ≤1 |
||||
1 |
|
|
|||||||||
f (x) = |
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
+ 2x |
, |
|
|
1 ≤ x ≤ 2 |
||||
6 x − 5x |
|
|
|
|
|||||||
8. Определить порядок точности формулы численного дифференцирования
'' |
|
f0 − 2 f1 + f2 |
|
f1 |
= |
|
|
h2 |
|||
|
|
для функции
|
x |
, |
|
|
|
|
|
|
−1 ≤ x ≤0 |
e |
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
3 |
|
|
f (x) = |
|
|
x |
|
x |
|
|
||
1 |
+ x + |
|
+ |
|
, |
0 ≤ x ≤1 |
|||
|
|
|
|
||||||
|
|
2 |
6 |
|
|
||||
Указания и ответы.
1. Использовать для представления функции интерполяционный многочлен в форме Ньютона.
3.a) R(x) = − |
|
h2 |
f ′′′(x) , b) R(x) = |
h2 |
|
f ′′′(x) , c) R(x) = |
h3 |
f (IV ) (x) |
|
|||||||
6 |
|
3 |
|
12 |
|
|||||||||||
d) R(x) = − |
|
h3 |
|
(IV ) |
|
|
|
′′′ |
|
|
h2 |
|
(IV ) |
(x) , |
||
|
12 f |
|
|
|
|
|
12 f |
|||||||||
|
|
(x) , 4.a) R(x) = −hf (x) , b) R(x) = − |
|
|||||||||||||
c) R(x) = |
11 |
|
h2 |
f (IV ) (x) , d) R(x) = |
11 h2 f (IV ) (x) . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
12 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||
37
V. Приближенное вычисление определенных интегралов
Наиболее часто используемый метод численного интегрирования основан на замене подынтегральной функции интерполированной.
f(x)
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2 |
|
x |
|
xi+k |
xn |
|||
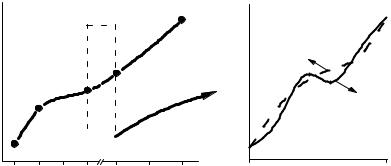
|
i |
|||||||
a)
|
Lk(x) |
|
f(x) |
xi |
xi +k |
|
b) |
Рис. 7
Пусть требуется вычислить интеграл
I = b∫ f (x)dx
a
от функции, заданной на [a, b] значениями f0, f1, …, fn в n узловых точках x0, x1, …, xn. Разобьем [a, b] на m отрезков, которые могут содержать несколько узлов (рис.7a). Тогда
m |
m |
I = ∑Ii = ∑ |
|
i=1 |
i=1 |
xi+k
∫ f (x)dx .
xi
На каждом отрезке [xi , xi+k ], содержащем k узлов, составляем интерполяционный многочлен Lk(x) (рис. 7b), и заменяя подынтегральную функцию f(x) ≈ Lk(x), получим
xi+k |
k |
|
Ii = ∫Lk (x)dx = ∑ A j fi+ j + r , |
(1) |
|
xi |
j=0 |
|
где Aj – коэффициенты, зависящие только от выбора узлов, но не от функции f, r – погрешность. Суммируя выражения (1) по всем отрезкам, получаем квадратурную формулу:
n
I= ∑Ai fi + R .
i=0
Здесь R – погрешность квадратурной формулы. Рассмотрим некоторые простые квадратурные формулы на равномерной сетке.
38
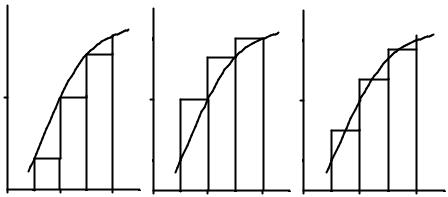
1. Формулы прямоугольников
Простейшие формулы получаются в том случае, когда в качестве интерполирующей функции берется константа (интерполирование проводится по одной точке). В данном случае функция f(x) заменяется ступенчатой функцией (рис. 8). Если интерполяция проводится по левой (правой) точке отрезка [xi,xi+1], то квадратурные формулы имеют вид соответственно (рис. 8a, b):
b∫ f (x)dx = h ( f0 + f1 +... + fn−1) |
(2) |
a |
|
b∫ f (x)dx = h ( f1 + f 2 +... + f n ) , |
(3) |
a |
|
где h = (b – a)/n.
Формула средних. Если в качестве интерполирующей точки выбирается средняя точка между xi и xi+1 (рис. 8с), то
b |
|
|
|
|
h |
|
|
|
|
h |
|
|
||
∫ |
|
|
|
|
|
|
||||||||
f (x)dx = h f x0 |
+ |
|
|
+ f x1 |
+ |
|
|
|
+…+ f |
xn−1 |
||||
|
|
2 |
||||||||||||
a |
|
|
|
|
2 |
|
|
|
|
|
|
|
||
где погрешность равна |
|
|
|
|
|
|
|
|
||||||
|
|
|
(b − a)h2 |
|
|
|
ξ [a, b] . |
|||||||
|
|
R = |
|
|
|
|
|
′′ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
24 |
|
f (ξ), |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ |
h |
|
+ R |
(4) |
|
|
|
||||
2 |
|||||
|
|
|
|
||
|
|
|
|
(5) |
Формула средних дает точное значение интеграла, если f(x) линейна.
f(x)
|
|
x |
x0 x1 x2 x3 |
x0 x1 x2 x3 |
x0 x1 x2 x3 |
a) |
b) |
c) |
2. Формула трапеций |
Рис. 8 |
|
|
|
Интерполирование исходной функции по двум точкам в промежутке [xi , xi+1 ] между соседними узлами приводит к замене f(x) от-
39
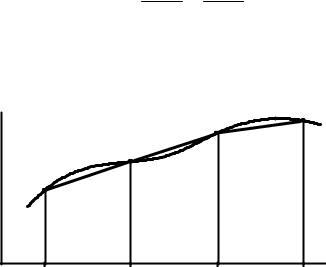
резком прямой, а на отрезке [a, b] – ломаной кривой (рис. 9). На равномерной сетке интеграл по формуле трапеций равен
b |
|
|
f |
0 |
|
|
|
|
|
f |
n |
|
+ R . |
(6) |
|
∫ |
f (x)dx = h |
|
|
|
+ f1 +…+ fn−1 |
+ |
|
|
|
||||||
|
2 |
|
|
|
|||||||||||
a |
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность формулы трапеций (6) равна |
|
|
|
|
|
|
|
||||||||
|
|
(b − a)h2 |
|
′′ |
|
|
|
|
|
|
(7) |
||||
|
R = − 12 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
f (ξ), ξ [a, b] . |
|
|
|
|
||||||
Формула трапеций является точной для линейной функции f(x), но ее погрешность вдвое выше погрешности формулы средних.
3. Формула Симпсона
Квадратурная формула Симпсона на равномерной сетке имеет вид:
b |
|
h |
( f0 + 4 f1 + 2 f2 + 4 f3 + 2 f4 +... + 2 fn−2 + 4 fn−1 + fn ) , (8) |
|
∫ |
f (x)dx = |
|||
|
||||
a |
3 |
|
||
|
|
|
||
где шаг равен
h = b −n a = b2−ma .
Здесь интерполяция проводится квадратичным многочленом по трем соседним узлам xi , xi+1 , xi+2 , вследствие этого общее разбиение отрезка должно быть таким, чтобы n = 2m было четным.
f(x) |
|
|
|
|
|
|
x |
x0 |
x1 |
x2 |
x3 |
|
|
Рис. 9 |
|
Погрешность квадратурной формулы Симпсона равна
R = − |
(b −a)h4 |
f (4)(ξ). |
(9) |
|
180 |
||||
|
|
|
Формула Симпсона является точной для подынтегральных функций, являющихся многочленами до третьей степени включительно.
Пример 1. Вычислить интеграл по формуле трапеций (n = 10) и формуле Симпсона (n = 10) и оценить погрешность вычислений,
40
