Выч.мат

Пример 4. Вычислить 2 с двумя правильными значениями после запятой.

Решение. Пусть y0 =1,5 , x = 2, тогда

Следующие приближения дают y3 = 2.1544, y4 = 2.1544. С указанной точностью значение 3 10 = 2,154.

2.3. Вычисление корня m–ой степени. Пусть есть функция y = m x .

Полагаем F(x, y)= ym − x . Тогда Fy′ (x, y)= mym−1 . Итерационная формула имеет вид

запятой.

Решение. x = 10, m = 5. Корень лежит между 1 и 2. Если выбрать y0 = 1 то y1 > 2. Поэтому выбираем y0 = 2. Тогда

Следующие итерации дают y3 = 1.5854, y4 = 1.5849, y5 = 1.5849. С

учетом округления 5 10 =1,585.

11

2.4. Сходимость итерационного процесса. Итерационный процесс

(8) – это алгоритм поиска корня уравнения F(x, y) = 0, т.е. точки пересечения графика F(x, y) с осью y. Формула (8) имеет простой геометрический смысл. Построим график F(x,y) в зависимости от y (x здесь играет роль постоянного параметра). Пусть y0 − начальное приближение. Из геометрического смысла параметров, входящих в соотношение (8),

Fy′ ( y0 ) = tgα , y0 − y1 = F ( y0 ) / tgα

находим, что на первом этапе приближение y1 определяется как точка пересечения касательной к F(y) в точке y0 с осью y (рис.1).

В следующем приближении эта процедура повторяется, и в случае сходимости последовательность yn стремится к точке пересечения

функции F(y) с осью y. Итерационный процесс (8) сходится к решению y , если

В частности, для процедуры вычисления квадратного корня согласно итерационному процессу (9) это дает следующее условие

сходимости ( y = x F = y2 − x F ′ = 2 y F ′′ = 2 ):

| y2 − x | < 2 y2 .

Отсюда находим, что все точки yn (n = 0,1,2,…) должны лежать в

области y > y / 3 , где y = x .

Следует иметь в виду, что неравенство (10) является достаточно жестким условием, которое выделяет только область монотонной сходимости последовательности yn (n = 0,1,2,…). Действительно, соотношение

12

| yn+1 − y | < | yn − y | означает, что каждое последующее приближение расположено ближе к точному значению y , чем предыдущее. И дан-

ный пример показывает, что условие монотонной сходимости (10) может определять не всю возможную область сходимости. В действительности итерационный процесс (9) вычисления квадратного корня сходится при всех y0 > 0 .

F(y)

Рис.2 Как видно из рис.2, если в качестве начального приближения выбрать

точку y0 левее значения y , то после первой же итерации значение y1

попадает в область монотонной сходимости, причем на первой итерации монотонности может и не быть. Здесь немонотонность сходимости итерационного процесса можно включить в рассмотрение следующим образом. К обеим частям равенства (9) добавим величины

x и − x . После элементарных преобразований получим два равен-

Отсюда находим отклонение yn от x :

13

Итерационный процесс сходится, если |q| < 1, т.е. y0 > 0. Из равенства (12) видно, что независимо от начального приближения y0 все yn ≥

x , если n ≥ 1, и для этих элементов последовательности имеем

Таким образом, здесь гарантированная монотонная сходимость процесса имеет место лишь при n ≥ 1.

Задачи

1.Пользуясь разложением в ряд функции f(x) = sin x, найти степенную функцию, аппроксимирующую f(x) в промежутке 0 ≤ x ≤ 1 с четырьмя правильными знаками.

2.Пользуясь разложением в ряд функции f(x) = ch x, найти степен-

ную функцию, аппроксимирующую f(x) в промежутке 0 ≤ x ≤ 1 с точностью ε = 10 − 3.

3. Используя разложение функции Бесселя Jn(x) в ряд

построить степенную функцию, аппроксимирующую J1(x) в промежутке 0 ≤ x ≤ 2 с точностью ε = 10 − 4.

4. Определить количество слагаемых в рядах

необходимое для вычисления суммы с точностью ε = 10−4. 5. Показать, что для ряда

∑∞ n13

n=1

остаток равен

Rn = n(n1+ 1) + o(1 / n2 ) .

6. Для вычисления значения обратной величины y = 1/x, согласно формуле (7), можно построить итерационный процесс

14

yn+1 = yn (2 − xyn),

если выбрать F(x,y) = x – 1/y. Найти условия, при которых этот процесс сходится.

7. Показать, что итерационный процесс вычисления квадратного

корня y = x вида yn+1 = x/yn не сходится.

8. Найти условие сходимости итерационного процесса вычисления корня y = x по формуле

Ответы и указания.

1 – 3. Воспользоваться оценками погрешности (2), (4) и (5).

1. f(x) = x – 0.16667 x3 +0.00833 x5 – 0.0002 x7.

4. a) n = 10000, b) n = 100. 6. y0 < 2/x. 8. y0 < 3x .

III.Интерполяция функций и погрешность интерполяции

1. Постановка задача интерполяции

Задача интерполяции ставится следующим образом. Пусть на числовой прямой заданы n+1 точка x0, x1, …, xn, которые называются узлами интерполирования. И пусть в узлах заданы значения функций f0, f1, …, fn, где fi = f(xi). Необходимо найти многочлен Ln(x) степени не выше n, значения которого в узлах совпадают со значениями исходной функции, т.е.

Многочлен Ln(x) называется интерполяционным многочленом и для табличной функции fi этот многочлен дает непрерывный аналог функции. Совокупность точек xi, i = 0,1,.., n называется сеткой, расстояние между соседними точками xi+1 –xi = hi есть шаг, и если точки расположены на равных расстояниях друг от друга, т.е. xi+1 – xi = h = const, то сетка называется равномерной.

В лагранжевой интерполяции предполагается, что все узлы различны, следовательно, их можно упорядочить в монотонную последовательность x0 < x1 < …< xn ( или x0 > x1 > …> xn). Далее будут рассматриваться такие последовательности узлов.

2. Интерполяционный многочлен в форме Лагранжа.

Такая задача имеет единственное решение и интерполяционный многочлен, записанный в форме Лагранжа, имеет вид:

15

Если функция f(x) задана аналитически, то многочлен Лагранжа в диапазоне [x0, xn ] дает приближение исходной функции

при условии, что в узлах выполняется (1). Геометрически это означает, что в соответствии с (2) через узловые точки проводится алгебраическая кривая вида (рис. 3):

Ln (x) = a0 xn + a1 xn−1 +... + an .

Многочлен Лагранжа построен, исходя из предположения, что значение многочлена в узле совпадает со значением функции. В про-

межутках между узлами Ln (x) и f (x) могут отличаться, и для от-

клонения между этими функциями (погрешность интерполяции) имеет место оценка

В частности, как следует из (4), лагранжев многочлен в точности воспроизводит функцию, которая является алгебраическим многочленом, степень которого не превышает степень многочлена Ln(x).

x

Рис.3 Линейная интерполяция. Здесь интерполяция функции производится по двум точкам x0 и x1 (n=1)

16

Наибольшая погрешность линейной интерполиции равна

где h – шаг сетки интерполирования. Отсюда имеем выражение для наибольшей погрешности

Пример 1. Какова наибольшая погрешность линейной интерполяции таблицы функции синусов с шагом 1°.

Решение. Для функции f = sinx имеем | f ” | = | sinx | ≤ 1. Шагу 1° соответствует h = π /180. Отсюда в соответствии с (5) имеем

RM =π 2 8 180 2 = 0.36 10 −4 .

3. Интерполяционный многочлен в форме Ньютона

С точки зрения результата интерполирования многочлены Лагранжа и Ньютона абсолютно идентичны, это разные формы записи одного и того же многочлена. Погрешность формулы (6) можно записать в виде:

Rn (x) = f (x)− Ln (x)= f (x, x0 , x1 ,…, xn )ωn (x)

Несмотря на кажущуюся громоздкость многочлена Ньютона, он во многих отношениях удобнее многочлена Лагранжа. Например, вычисление значений функции в произвольной точке диапазона [x0 xn] проводят с помощью интерполяционных таблиц вида:

17

Впервую и вторую колонку заносятся значения аргумента и функции.

Втретью колонку заносятся разделенные разности первого порядка, которые вычисляются по данным первых двух колонок. Разделенные разности n-ой колонки вычисляется по данным первой и (n-1)-ой ко-

лонки. В формулу многочлена Ньютона (6) подставляются данные верхней диагонали таблицы.

Пример 2. Составим таблицу разностей функции f = 2x 2 на равномерной сетке с шагом 1, начинающейся с x0 =1.

14

4 32

Видно, что таблица разностей обрывается на третьем шаге. При этом интерполяционный многочлен имеет вид

Ln (x)= 2 +(x −1)6 +(x −1)(x −2)2 = 2 +6x −6 + 2(x 2 −3x + 2)= 2x 2

В полном соответствии с выводом о том, что интерполяционный многочлен является точным для функции в виде полинома, если в рассмотрение включено достаточное число узлов. Таким образом, если в таблице происходит обрыв, то интерполируемая функция – многочлен степени, соответствующей номеру неисчезающей разности в таблице.

Пример 3. Пусть функция будет та же f = 2x 2 , равномерная сетка с шагом 2, начинающаяся с x0 =0.

20

6 72

Добавим в эту таблицу еще одну координату x =5

18

Видим, что изменения в таблице минимальны, и касаются только трех элементов, а верхняя диагональ вообще не изменилась. Многочлен в форме Ньютона выгодно отличается от лагранжевой формы записи тем, что при добавлении новых точек не приходится пересчитывать всю таблицу.

Тогда sin в этом диапазоне углов будет вычисляться по формуле f (x)= f0 + xf (1) + x(x −1)f (2) + x(x −1)(x − 2)f (3) .

Например, для ϕ =45° имеем x = 1,5 и значение функции равно

f (1,5)=1,5 0,5–1,5 0,5 0,067 +1,5 0,5 0,5 0,016 = 0,75−0,05 + 0,006=0,706.

Это значение близко к табличному значению sin 45° = 0,707. По таблице разностей легко контролировать сходимость. Быстрое убывание членов ряда обеспечивает хорошую точность задачи интерполирования.

Пример 5. Влияние погрешности задания сеточной функции. Пусть в примере 1 одна из функций определена с ошибкой. f =2x2 x0=1 h=1.

19

Результатом интерполяции будет выражение

Ln (x) = 2x2 + ε(−x3 +7 x2 −14x + 8) / 2 = 2x2 + r .

Например, при x = 5 имеем r = − 6ε. Таким образом, малозаметная ошибка на начальной стадии вычисления может стать существенной в конце таблицы. По этой причине при интерполяции берут небольшое число узлов.

4. Обратное интерполирование

В задаче интерполирования совокупность значений аргументов xi и совокупность значений функций fi равноправны. Ранее были построены интерполяционные многочлены для функций по значени-

В данном случае производится интерполирование обратной функции x(f). С помощью формулы (7) обратной интерполяции можно решать трансцендентные и алгебраические уравнения, при этом необходимо учитывать, что функция x(f) должна быть однозначной. Другим способом определения корня уравнения является использование формулы прямого интерполирования (6):

f (x)= f0 + (x − x0 )f (1) + (x − x0 )(x − x1 )f (2) +...

... + (x − x0 )(x − x1 )...(x − xn−1 )f (n)

Здесь f (n) – разделенная разность n –го порядка. Полагая в последнем равенстве f (x) = 0 и выделяя, например, линейное слагаемое, имеем

(8)

Это соотношение рассматриваем как новое функциональное равенство x = g(x), которое можно решить методом последо-вательных приближений. В качестве начального приближения x(0) выбирается свободный член уравнения

x(0) = (x0 f (1) − f0 )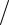 f (1) .

Значение следующего приближения определяется из (8) после подстановки в него x (0): x (1) = g(x (0)). Этот процесс продолжается до

20