Десятичная система счисления. Одна и та же цифра в позиционной системе счисления имеет разное значение в зависимости от того, где эта цифра находится в числе.
Двоичная система счисления
Восьмеричная система счисления
Шестнадцатеричная система счисления содержит 16 цифр - это цифры от 0 до 9 (соответствуют десятичным цифрам) и буквы от A до F, соответствие которых десятичным эквивалентам можно запомнить, а можно каждый раз в уме подсчитывать (1010 - это А16, 1110 - это B16, 1210 - это C16, 1310 - это D16, 1410 - это E16, а 1510 - это F16)
Основные правила перевода:
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой.
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой.
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
13. Двоичная система счисления как базовая система представления и хранения числовой информации в компьютере. Единицы двоичной информации и их назначение: бит, байт, машинное слово.
В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц, поэтому компьютер может обрабатывать только информацию, представленную в цифровой форме. В цифровых устройствах Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям: Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.
Для преобразования числовой, текстовой, графической, звуковой информации в цифровую необходимо применить кодирование. Кодирование – это преобразование данных одного типа через данные другого типа. В ЭВМ применяется система двоичного кодирования, основанная на представлении данных последовательностью двух знаков: 1 и 0, которые называются двоичными цифрами (binarydigit – сокращенно bit). Таким образом, единицей информации в компьютере является один бит, т.е. двоичный разряд, который может принимать значение 0 или 1. Восемь последовательных бит составляют байт. В одном байте можно закодировать значение одного символа из 256 возможных (256 = 2 в степени 8).
Машинное слово - упорядоченный набор цифр, букв и т. д., хранящихся в памяти ЭВМ и воспринимаемых при обработке устройствами машины как единое слово, команда. Количество основных символов в машинном слове называется длиной слова; обычно машинное слово содержит целое число байтов.
14. Форматы хранения чисел в компьютере. Прямой, обратный, дополнительный коды чисел. Форматы хранения символьной информации. Американский стандартный код обмена информации (ASСII). Форматы хранения графической видео- и аудио информации.
Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, то есть вне разрядной сетки. Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2= 111100002будет храниться в ячейке памяти следующим образом:
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно2- 1.Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно А = 1×27+ 1×26+ 1×25+ 1×24+ 1×23+ 1×22+ 1×21+ 1×20= 1×28- 1 = 25510. Диапазон изменения целых неотрицательных чисел: от 0 до 255.Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное1).Представление в компьютере положительных чисел с использованием формата знак-величина называется прямым кодом числа. Например, число 200210 = 111110100102 будет представлено в 16-разрядном представлении следующим образом:
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:А = 2n-1- 1.Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2n- |A|.Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, так как в n-разрядной компьютерной арифметике:2n- |А| + |А| = 0,поскольку в компьютерной n-разрядной арифметике 2n= 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей. Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:1. Модуль числа записать в прямом коде в n двоичных разрядах.2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).3. К полученному обратному коду прибавить единицу. Запишем дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления: |
| ||||||||||||||
При n-разрядном представлении отрицательного числа А в дополнительным коде старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число2n-1- |А|.Чтобы число было положительным, должно выполняться условие|А|£2n-1.Следовательно, максимальное значение модуля числа А в га-разрядном представлении равно:|А| = 2n-1.Тогда минимальное отрицательное число равно:А = - 2n-1.Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится четыре ячейки памяти - 32 бита).Максимальное положительное целое число (с учетом выделения одного разряда на знак) равно:А = 231- 1 = 2 147 483 64710.Минимальное отрицательное целое число равно:А = -231= - 2 147 483 64810.Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций. Недостатком представления чисел в формате с фиксированной запятой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.
Представление чисел в формате с плавающей запятой. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде
|
A = m×qn |
|
где m - мантисса числа;q - основание системы счисления; n - порядок числа.Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:1/n |m| < 1.Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля. Преобразуем десятичное число 555,55, записанное в естественной форме, в экспоненциальную форму с нормализованной мантиссой:555,55 = 0,55555×103.Здесь нормализованная мантисса: m = 0,55555, порядок: n = 3.Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.Определим максимальное число и его точность для формата чисел обычной точности, если для хранения порядка и его знака отводится 8 разрядов, а для хранения мантиссы и ее знака - 24 разряда:
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 | ||
|
знак и порядок |
знак и мантисса |
| |||||||||||||||||||||||
Максимальное значение порядка числа составит 11111112= 12710, и, с.Максимальное значение положительной мантиссы равно:223- 1»223= 2(10×2,3)»10002,3= 10(3×2,3)»107.Таким образом максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411×1038(количество значащих цифр десятичного числа в данном случае ограничено 7 разрядами.
Прямой, обратный, дополнительный коды чисел. Прямой код числа образуется кодированием знака числа нулём, если число положительно и единицей, если число отрицательно (для двоичной системы) Для общего случая (q - 1) - если число отрицательно, и 0 - если число положительно. q - основание системы счисления. Код знака записывается перед старшей цифрой числа и отделяется от неё точкой:-1.01 = 1.101 Прямой, обратный и дополнительный коды положительных чисел совпадают между собой.
Обратный код отрицательного числа образуется из прямого кода, заменой его цифр на их дополнения до величины q-1. Код знака сохраняется без изменения. Замена цифр их дополнениями для двоичной системы совпадает с операцией инверсии, то есть нули заменяются единицами, единицы - нулями. Знак принимает значение, равное единице.
Дополнительный код отрицательного числа образуется из обратного увеличением на 1 его младшего разряда. При этом перенос из знакового разряда игнорируется. Правила перевода из прямого кода в обратный и из обратного в прямой, а также из прямого в дополнительный и из дополнительного в прямой совпадают между собой.
Форматы хранения символьной информации. Для кодирования символьной или текстовой информации применяются различные системы: при вводе информации с клавиатуры кодирование происходит при нажатии клавиши, на которой изображен требуемый символ, при этом в клавиатуре вырабатывается так называемый scan-код, представляющий собой двоичное число, равное порядковому номеру клавиши.Номер нажатой клавиши никак не связан с формой символа, нанесенного на клавише. Опознание символа и присвоение ему внутреннего кода ЭВМ производятся специальной программой по специальным таблицам: ДКОИ, КОИ-7, ASCII.
Американский стандартный код обмена информации (ASСII). ASCII представляет собой обычный цифровой код для компьютеров и других устройств, работающих с текстом. Компьютеры могут понимать только числа, поэтому код ASCII является представлением символа, например, 'a' или '@' в числовой форме. Упоминание ASCII в связи с доменными именами или последовательностями относится к тому факту, что до интернационализации в доменных именах были разрешены только буквы a-z, цифры 0-9 и дефис "-".
Форматы хранения графической видео- и аудио информации. Графический формат — это способ записи графической информации. Графические форматы файлов предназначены для хранения изображений, таких как фотографии и рисунки.
Хранение видеоинформации в различных форматах (потоковое и файловое хранение). До недавнего времени основным форматом сжатия видеоинформации в видеокамерах был формат MJPEG, в котором видеопоток представляет собой последовательность отдельных видеокадров формата JPEG. С точки зрения файловой системы компьютера видеопоток разбивался на отдельные файлы, каждый из которых содержал один кадр в формате JPEG.При просмотре система показывает пользователю последовательность кадров, меняющуюся с определенной частотой, в результате, как в кинотеатре, получается непрерывное движущееся изображение.С появление формата H.264 он де-факто становится вторым (а иногда и первым) стандартом для камер видеонаблюдения. В отличие от формата MJPEG, формат H.264 оперирует последовательностью видеокадров. Первый кадр является опорным, а во втором передается не вся «картинка», а лишь изменения, которые произошли по сравнению с опорным кадром и т.д. В результате объем передаваемой информации по сравнению с форматом MJPEG уменьшается в 10-20 раз. Чем длиннее цепочка видеокадров, тем больше получаемый выигрыш. Именно поэтому видео в формате H.264 сохраняется не в виде отдельных кадров, а в виде достаточно продолжительных «видеофильмов» (потоковое видео).Видеосистема XViewsion может свободно оперировать с видеопотоками обоих форматов, предоставляя пользователям полный функционал как для видео в формате MJPEG, так и в формате H.264.
Цифровой аудиоформат — формат представления звуковых данных, используемый при цифровой звукозаписи, а также для дальнейшего хранения записанного материала на компьютере и других электронных носителях информации, так называемых звуковых носителях.
15. Машинный формат хранения вещественных чисел с плавающей запятой. Для вычислений с большими величинами числа с фиксированной запятой неэффективны. В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:
0,2×105;
0,16×10-38
Для записи двоичных чисел тоже используется такая форма записи. Эта форма записи называется запись числа с плавающей точкой. Напомним, что мантисса не может быть больше единицы и после запятой в мантиссе не может записываться ноль.
А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырёхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены на рисунке
16. Информационные сети. Классификация сетей.
ИС – это коммуникационная сеть, в которой продуктом генерирования, переработки, хранения и использования является информация. Вычислительная сеть – это ИС, в состав которой входит вычислительной оборудование. Основные характеристики сети, её структура и особенности определяются архитектурой.
Классификация ВС по расстоянию между узлами
А)Локальные – ограниченная территория, расстояние до 1 км
Б)Корпоративные (в масштабах предприятия) – совокупность ВС одного предприятия, расположенных в соседних зданиях
В)Территориальные:
- региональные
- глобальные(Интернет)
Интернет – это глобадьная телекоммуникационная информационная сеть, объединяющая десятки тысяч локальных сетей ЭВМ, сотни стран, миллионы узлов и сотни миллионов пользователей.
В зависимости от технологии передачи данных различают · сети с маршрутизацией данных (каждый блок данных передаётся только одной системе-адресату) · сети с селекцией данных (каждый блок данных передаётся всем системам).
Кроме того, различают:
· коммуникационные сети. Предназначены для передачи данных, могут также обеспечивать выполнение задач, связанных с преобразованием данных (сборкой символов в пакеты, обеспечение достоверности передачи и т.д.);
· информационные сети. Они получаются подключением к коммуникационной сети абонентских систем. При этом на базе коммуникационной сети может быть построена не одна, а группа информационных сетей.
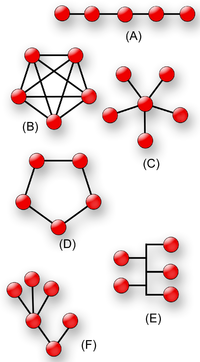
17. Топология сети — способ описания конфигурации сети, схема расположения и соединения сетевых устройств.
Сетевая топология может быть
физической — описывает реальное расположение и связи между узлами сети.
логической — описывает хождение сигнала в рамках физической топологии.
информационной — описывает направление потоков информации, передаваемых по сети.
управления обменом — это принцип передачи права на пользование сетью.
Существует множество способов соединения сетевых устройств. Выделяют 3 базовых топологии:
Шина
Кольцо
Звезда
И дополнительные (производные):
Двойное кольцо
Ячеистая топология
Решётка
Дерево
FatTree
Снежинка
Полносвязная
Дополнительные способы являются комбинациями базовых. В общем случае такие топологии называются смешанными или гибридными, но некоторые из них имеют собственные названия, например «Дерево».