
Shpory_1
.doc|
1 Уравнения первого порядка, разрешённые относительно производных. Их геометрическая интерпретация. Рассмотрим
уравнение 1-го порядка вида
Общим
решением уравнения
Решение
уравнения
Решение, не являющееся частным решением, называется особым решением.
Геометрически
решению уравнения
Для
уравнения
Уравнение
Геометрически
решить уравнение
Изоклина – геометрическое место точек, в каждой точке которых векторы равны.
В
дальнейшем будем считать, что переменные
x
и y
в уравнении
Часто
не удаётся получить решение уравнения
|
2 Уравнение с разделяющимися переменными.
Рассмотрим
уравнение
Т1.
Пусть
Условие
Условие
Условие
единственности
Уравнение
|
3 Уравнения в полных дифференциалах. Интегрирующий множитель.
Рассмотрим
уравнение
Пусть
Функция
Таким образом, общий интеграл уравнения можно получить, построив первый интеграл.
В
случае односвязной области D
уравнение
Пусть
уравнение
Если
Заметим, что полученное уравнение является уравнением с частными производными I-го порядка. Решение такого уравнения в общем случае может оказаться более сложной задачей, чем решение исходного уравнения. Нас интересует только одно решение этого уравнения и в некоторых случаях его можно подобрать.
|
|
4 Линейные уравнения первого порядка.
Линейными
уравнениями I-го
порядка будем называть уравнения вида
Если
Будем полагать,
что функции
Пусть
Линейное уравнение
всегда имеет интегрирующий множитель
Способы решения линейных уравнений:
Следовательно,
решение задачи Коши легко получить
соответствующим
Общие свойства линейных уравнений:
|
5. Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной. Особые точки. Особые решения
Рассмотрим
уравнение
Пусть
функция
Эта
теорема часто называется теоремой
Пикара. В ней непрерывность функции
При
условиях теоремы уравнение
Приведённая теорема позволяет выделять множество так называемых обыкновенных точек:
Точка
Точка
Особые точки:
Особая
точка
Если из особых точек составлена линия, то такая линия называется особой линией. Если особая линия является интегральной линией, то она называется особой интегральной линией. Решение уравнения, соответствующее особой интегральной линии – особое решение.
Классическим
примером особой интегральной линии
является огибающая семейства
интегральных линий (например,
|
6. Уравнения первого порядка, не разрешённые относительно производной.
В
общем случае уравнения первого порядка
представляются в виде
Уравнением,
не разрешённым относительно производной,
называют уравнение вида
Рассмотрим
уравнение вида
Задача
Коши называется корректно поставленной,
если через точку
В
случае, когда задача Коши поставлена
корректно, решение этой задачи можно
выделить однозначно, дополнительно
указав угловой коэффициент. Выбор
углового коэффициента можно произвести,
решая конечное уравнение
Пусть
Методы решения:
Для уравнений, неразрешённых относительно производной также можно ввести понятие особой точки, особого решения.
|
|
7 Теорема о существовании и единственности решения задачи Коши для уравнения порядка выше первого.
В
общем случае уравнения порядка выше
первого представляются в виде
Пусть
функция f
непрерывна в D
и имеет в D
непрерывные производные по всем
аргументам, начиная со второго. Тогда
найдётся отрезок
При
условиях теоремы общее решение
уравнения
Для
доказательства теоремы часто уравнение
Отметим,
что под решением уравнения
|
8 Линейные уравнения порядка n. Общие свойства линейных уравнений.
Под
линейными уравнением будем понимать
уравнение вида
Введём
формальный оператор
Общие свойства линейных уравнений:
Пусть
Пусть
Следствия дают программу дальнейших исследований. Первое следствие приведёт к общему решению однородного уравнения, а второе – к общему решению неоднородного уравнения.
Пусть
уравнение
В
дальнейшем будем полагать, что функции
Пусть
Пусть
функции
Далее
считаем, что
|
9 Решение однородных линейных уравнений
Пусть
на
9
Теорема о линейно зависимых функциях:
Пусть функции
Функции
Если
хотя бы в одной точке
10
Теорема о линейно независимых решениях
однородного линейного ур-ия порядка
n.
ФСР:
Пусть
Система
линейно независимых решений
11
Теорема об общем решении однородного
линейного уравнения порядка n:
Пусть
Система
решений
Множество
решений линейного уравнения
Однородное линейное уравнение можно решить, построив ФСР. В общем случае уравнений с переменными коэффициентами общего метода построения ФСР нет. Возможно понижение порядка, если известно хотя бы одно нетривиальное решение уравнения. На этом пути в простейших случаях удаётся получить ФСР. Уравнения с постоянными коэффициентами решаются всегда. ФСР однородного уравнения с постоянными коэффициентами всегда можно решить методом Эйлера.
|

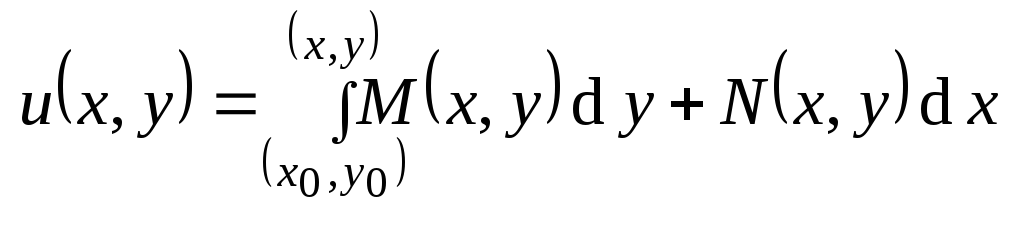 .
Здесь вычисляется криволинейный
интеграл II-го
рода по кривой, соединяющей точки
.
Здесь вычисляется криволинейный
интеграл II-го
рода по кривой, соединяющей точки
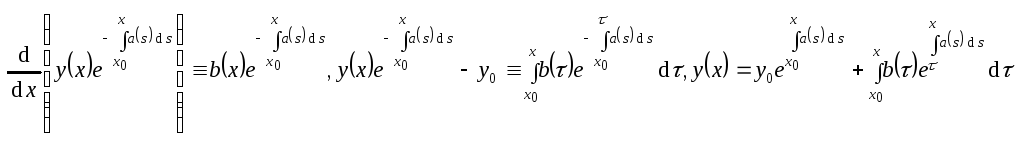 .
Таким образом, решение задачи Коши,
если оно существует, представляется
в виде этого тождества. Рассмотрим
его. В правой части имеем непрерывно
дифференцируемую функцию, определённую
при
.
Таким образом, решение задачи Коши,
если оно существует, представляется
в виде этого тождества. Рассмотрим
его. В правой части имеем непрерывно
дифференцируемую функцию, определённую
при
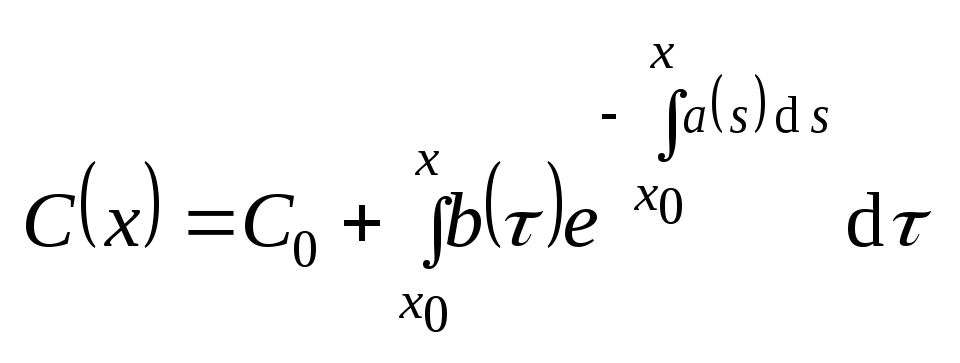 .
Подставим
.
Подставим
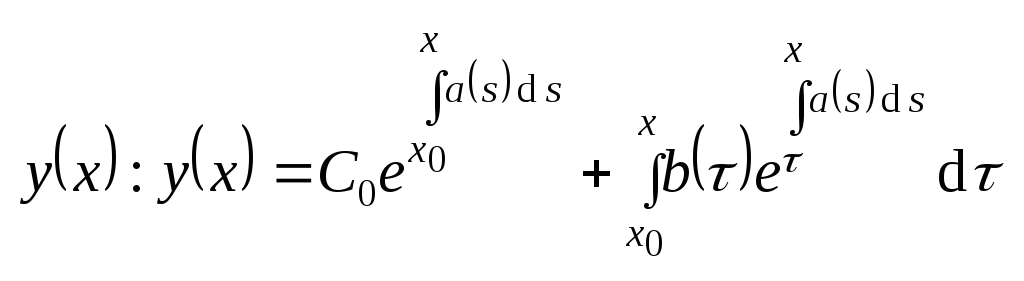 .
Здесь
.
Здесь
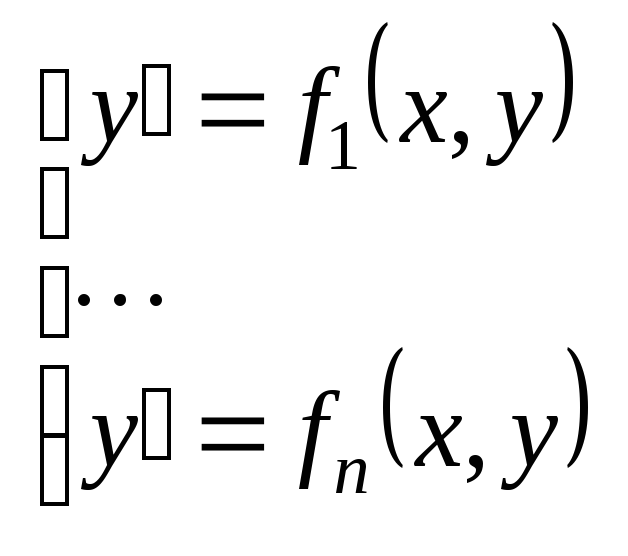 .
Решая эту систему, находим решение
исходного уравнения.
.
Решая эту систему, находим решение
исходного уравнения.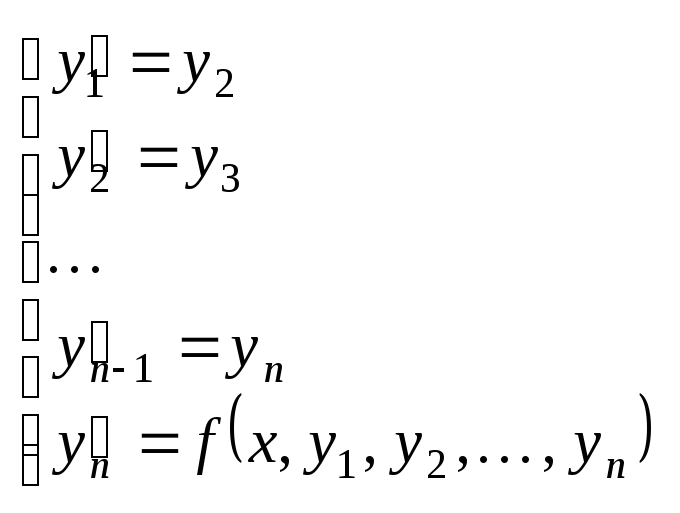 .
Начальные условия при этом принимают
вид:
.
Начальные условия при этом принимают
вид:
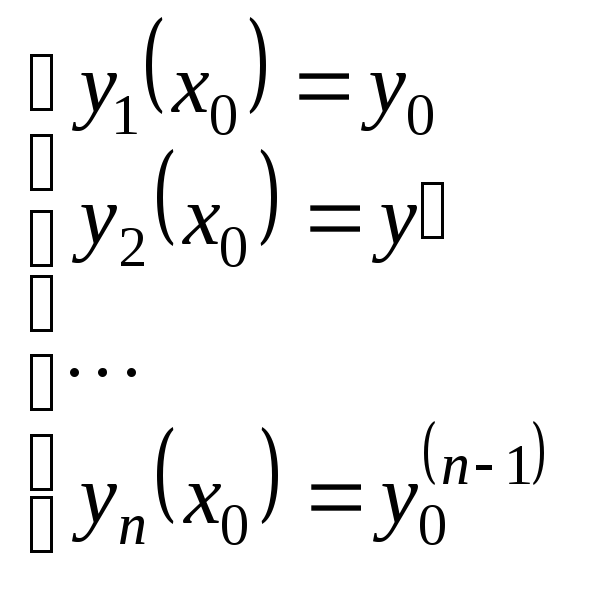 .
Таким образом, задача Коши сопоставляется
с другой задачей Коши, составленной
из новых переменных. Свойства системы
подобны свойствам уравнения, разрешённого
относительно производной из предыдущего
раздела. Поэтому она может быть
исследована прежними методами. Решив
эту задачу Коши, выберем компоненту
.
Таким образом, задача Коши сопоставляется
с другой задачей Коши, составленной
из новых переменных. Свойства системы
подобны свойствам уравнения, разрешённого
относительно производной из предыдущего
раздела. Поэтому она может быть
исследована прежними методами. Решив
эту задачу Коши, выберем компоненту
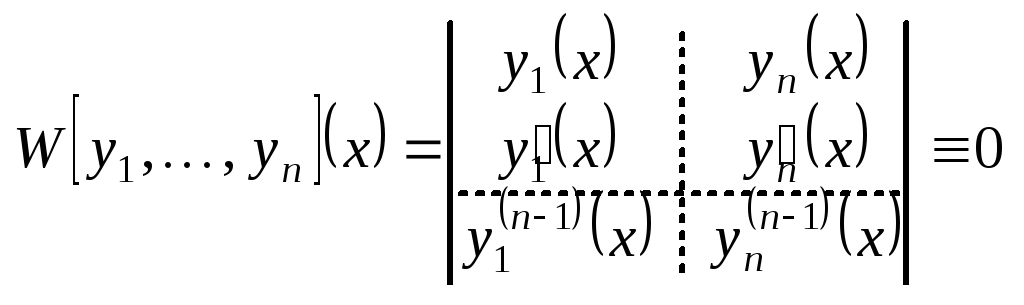 (определитель Вронского).
(определитель Вронского).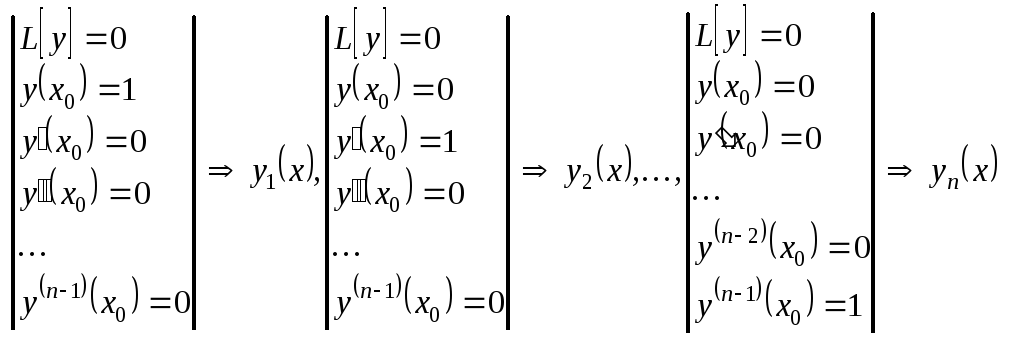 .
При этом
.
При этом
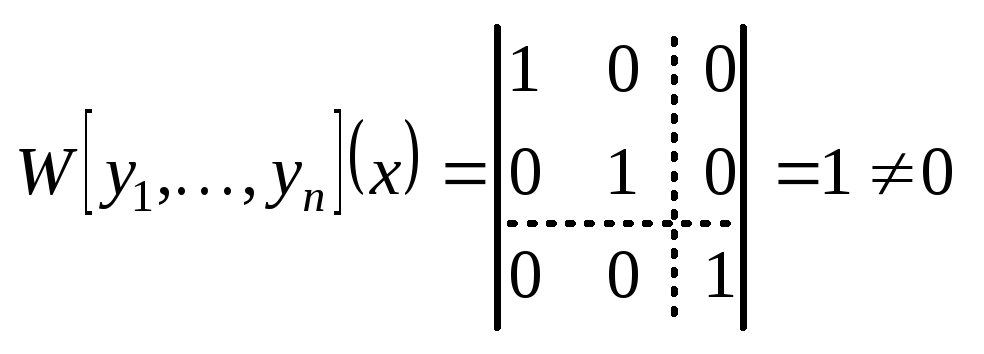 .
.